Рассмотренные свойства многомерных матриц позволяют сформулировать один принцип, который облегчает алгоритмизацию задач.
Сформулируем принцип последовательно-параллельного программирования в виде следующих четырех положений:
- в качестве базового типа данных используется алгебра многомерных матриц;
- операции этой алгебры реализуются как базовые процедуры обработки данных для конкретных суперкомпьютеров, с максимально допустимой степенью параллелизма;
- многомерные матрицы включаются как самостоятельные объекты;
- алгоритмы представляются как последовательности операций над многомерными матрицами.
Перечислим основные достоинства принципа последовательно-параллельного программирования.
Данные, представленные в виде многомерных матриц, последовательно обрабатываются операциями алгебры многомерных матриц как неделимые объекты.
Программа выполняется на суперкомпьютере параллельно, так как каждая операция над многомерными матрицами реализуется параллельным алгоритмом.
Представление информации посредством многомерных матриц, позволяет разрабатывать модели для различных предметных областей. Эти модели могут быть реализованы на суперкомпьютерах с минимальными затратами на программирование.
Одним из направлений использования метода последовательно-параллельного программирования являются экспертные системы. Многомерные матрицы представляют собой идеальное средство для классификации и представления правил адаптивного принятия решений.
Лабораторная работа
”Адаптивные преобразования фигуры в плоскостных
координатах”
Быстрое преобразование Уолша.
Функции Уолша обладают интересными свойствами, привлекающими к ним все большее внимание. Они принимают всего два значения {+1 или -1} и потому удобны для вычислений на ЭВМ. Существует различное упорядочение функций Уолша.Рассмотрим одну из возможных систем функций Уолша – систему Уолша-Адамара. Элементарная матрица Адамара, состоящая из одного элемента (N=1), имеет вид H1=[1]. Для N=2 элементами матрицы Адамара будут элементарные матрицы (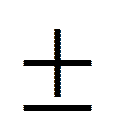 H1):
H1):

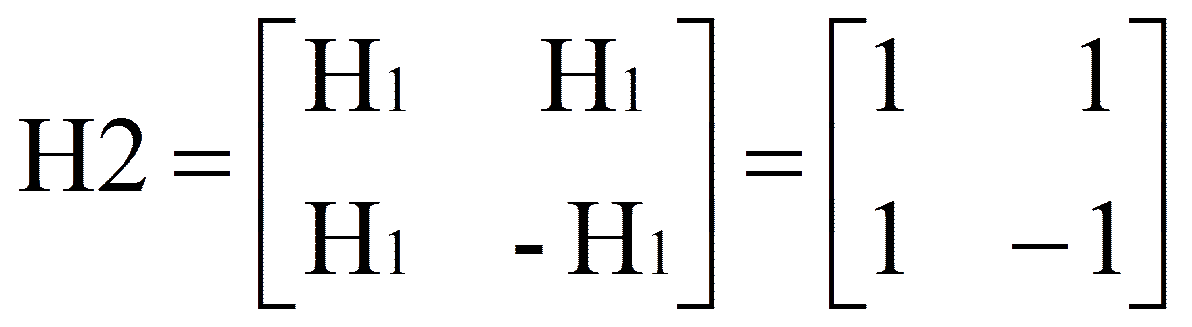 . Для N = 4 элементами матрицы Адамара будут матрицы (
. Для N = 4 элементами матрицы Адамара будут матрицы (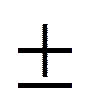 H2):
H2):

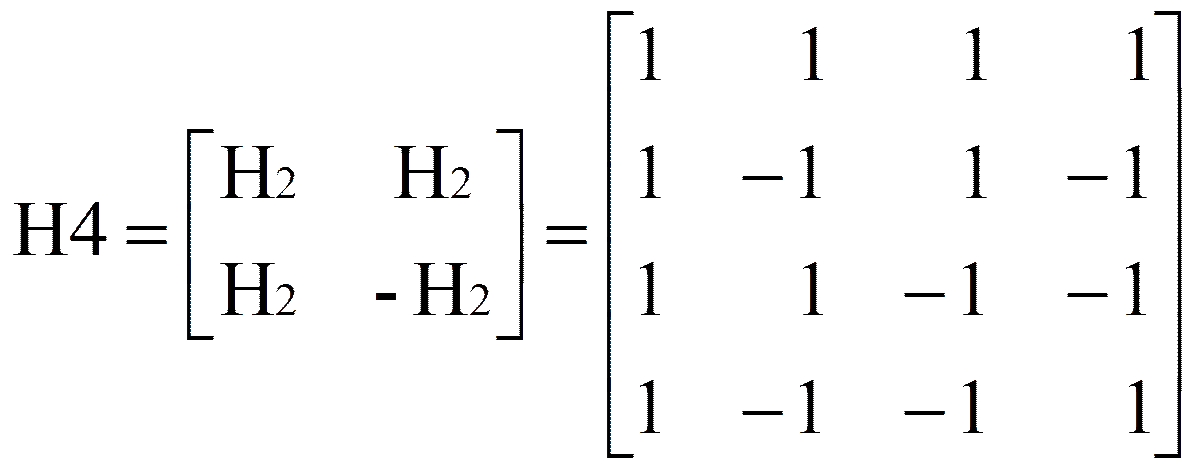 .
.
Для N=2n имеем 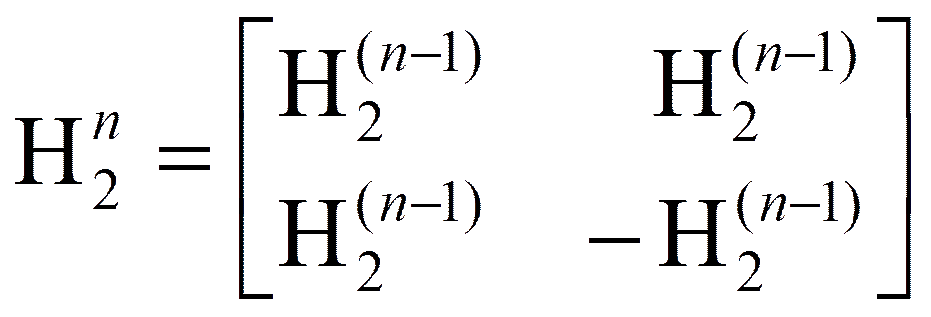 .
.
Дискретное преобразование Уолша, как и дискретное преобразование Фурье, представляется в матричной форме:
FY=HN*S/N; S= (HN)T*FY.
Здесь FY-коэффициенты спектрального разложения по функциям Уолша, S-дискретные временные отсчеты сигнала.
Быстрое преобразование Уолша (БПУ) можно получить из формулы для БПФ,исключив фазосдвигающие составляющие.
Матрица преобразований упрощается и имеет вид:
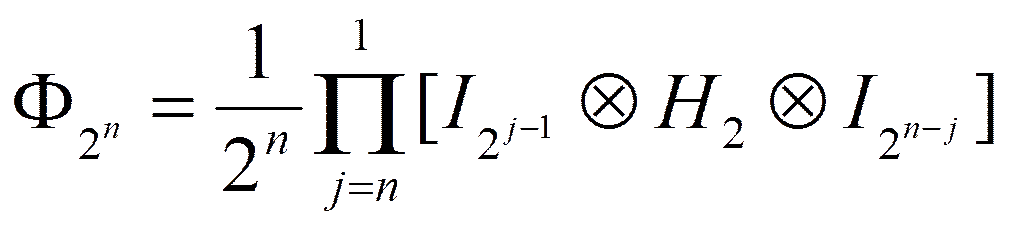 .
.
Коэффициенты спектрального разложения по функциям Уолша имеют прямую последовательность в отличие от БПФ, имеющей последовательность с двоично-инверсными номерами.
| №1
|
|
|
| перенос
|
|
|
|
|
|
|
|
|
|
|
| -49,421
| 190,938
|
|
| №2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -14,06
| 197,995
|
|
| №3
|
|
|
|
| -100
| -100
|
|
|
|
|
|
|
|
|
| 35,425
| 176,762
|
|
| №4
|
|
|
|
|
|
|
|
| -30
|
|
|
|
|
|
| 70,7782
| 169,677
|
|
| №5
|
|
|
|
|
|
|
|
| -70
|
|
|
|
|
|
| 56,60795
| 98,9724
|
|
| №6
|
|
|
|
|
|
|
| -20
| -50
|
|
|
|
|
|
| 21,2498
| 91,9154
|
|
| №7
|
|
|
|
|
|
|
| -30
| -20
|
|
|
|
|
|
| -7,028
| 106,068
|
|
| №8
|
|
|
|
|
|
|
| -40
|
|
|
|
|
|
|
| -49,44
| 134,37
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| растяжение
|
|
| вращение
|
|
|
|
|
|
| растяжение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| вращение
| 0,707388
| 0,706825
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -0,70683
| 0,707388
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| по X,Y
|
|
|
|
|
|
|
|
|
|
|
| базис
| уолша
|
|
|
|
|
|
| сдвиг
|
|
| растяжение
|
| вращение
|
|
|
|
|
|
|
|
|
|
|
|
| 870/8
|
|
| 1740/8
|
|
| 64,10415/8
|
|
|
|
|
| -1
|
| -1
|
| -1
|
| -1
|
| -10/8
|
|
| -20/8
|
|
| 7,062621/8
|
|
|
|
|
|
| -1
| -1
|
|
| -1
| -1
|
| -30/8
|
|
| -60/8
|
|
| -35,3582/8
|
|
|
|
|
| -1
| -1
|
|
| -1
| -1
|
|
| 10/8
|
|
| 20/8
|
|
| -7,06262/8
|
|
|
|
|
|
|
|
| -1
| -1
| -1
| -1
|
| 230/8
|
|
| 460/8
|
|
| 21,33427/8
|
|
|
|
|
| -1
|
| -1
| -1
|
| -1
|
|
| -90/8
|
|
| -180/8
|
|
| -148,484/8
|
|
|
|
|
|
| -1
| -1
| -1
| -1
|
|
|
| -150/8
|
|
| -300/8
|
|
| -304,019/8
|
|
|
|
|
| -1
| -1
|
| -1
|
|
| -1
|
| -30/8
|
|
| -60/8
|
|
| 7,051359/8
|
|
|
|
|
|
|
|
|
|
|
|
|
| обращен
| x
| y
|
| x
| y
|
| x
| y
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| -49,4215
|
|
|
|
| -1
|
| -1
|
| -1
|
| -1
|
|
|
|
|
|
|
|
| -14,0633
|
|
|
|
|
| -1
| -1
|
|
| -1
| -1
|
|
|
|
|
|
|
|
| 35,42572
|
|
|
|
| -1
| -1
|
|
| -1
| -1
|
|
|
|
|
|
|
|
|
| 70,77824
|
|
|
|
|
|
|
| -1
| -1
| -1
| -1
|
|
|
|
|
|
|
|
| 56,60795
|
|
|
|
| -1
|
| -1
| -1
|
| -1
|
|
|
|
|
|
|
|
|
| 21,2498
|
|
|
|
|
| -1
| -1
| -1
| -1
|
|
|
|
|
|
|
|
|
|
| -7,02884
|
|
|
|
| -1
| -1
|
| -1
|
|
| -1
|
|
|
|
|
|
|
|
| -49,444
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
*********************************************************
********************************************************************
Функции этого семейства являются производными гауссовой экспо-ненты:
()().,12/12 N ∈−=−+nedxdxgxnnnn (1–5)
Нормирующий коэффициент принимает значение
().0,!12∞<<−=nnCngπ
Свое название семейство VMWF-вейвлетов получило за то, что первые моментов функций 1−n()xgn равны нулю:
(1–6) ().,0,0 N ∈<≤∀=∫∞∞−nnmmdxxgxnm
Наиболее широко применяют гауссовы вейвлеты небольших порядков, которые выглядят следующим образом:
(),2/12xexxg−−= 16
()(),12/222xexxg−−=
()(),32/332xexxxg−−=
()().362/2442xexxxg−−+−=
На рис. 1–1 показано поведение этих функций. Некоторые свойства гауссо-вых вейвлетов подробно рассмотрены в [14, 23, 50].
а) б)
| в) г) Рис. 1–1.
| Гауссовы вейвлеты младших четырех порядков.
|
Вейвлет-преобразование ********************************************
Термин вейвлет-преобразование объединяет два вида преобразова-ний — прямое и обратное, которые, соответственно, переводят исследуемую функцию в набор вейвлет-коэффициентов ()xf()fbaW,ψ и обратно. Разли-чают непрерывное и дискретное преобразования, в дальнейшем мы ограничимся рассмотрением в основном непрерывного варианта.
Прямое вейвлет-преобразование осуществляется согласно правилу
()(),11,∫−=dxxfabxaCfbaWψψψ (1–1)
где a и b — параметры, определяющие соответственно масштаб и смещение функции,ψ называемой анализирующим вейвлетом, — нормировочный множитель. Интегрирование ведут по всей числовой оси. ψC
1 Уже после того, как это было написано, в продаже появился перевод книги К. Чуи по основам вейвлет-анализа. К сожалению, мои ожидания пока не сбылись. В издательстве Мир книга вышла под на-званием «Введение в вэйвлеты» [20]. 14
Базисный, или материнский вейвлет ψ образует посредством растяже-ний и сдвигов семейство −abxψ.
Имея известный набор коэффициентов (),,fbaψW можно восстановить исходный вид функции: ()xf
()()[].,112adbdafbaWabxaCxfψψψ−=∫∫ (1–2)
Прямое (1–1) и обратное (1–2) преобразования зависят от некоторой функции которую называют базисным вейвлетом. Практиче-ски единственным ограничением на его выбор является условие конечности нормировочного множителя ()(),2 R Lx∈ψ
()(),ˆ2ˆ022∞<==∫∫∞∞∞−ωωωψωωωψψddC (1–3)
где ()ωψˆ — Фурье-образ вейвлета ():xψ ()().21ˆ∫∞∞−−=dxexxiωψπωψ
Этому условию удовлетворяет множество функций, поэтому возможно подобрать вид вейвлета, наиболее подходящего для решения конкретной задачи.
Условие (1–3) неизбежно означает, что Фурье-образ вейвлета равен ну-лю при нулевой частоте, то есть ().0ˆ0==ωωψ ψЕсли это не так, то знаменатель дроби в интеграле (1–3) обращается в нуль, в то время как числитель имеет отличное от нуля значение, и коэффициент C перестает быть конечным.
В свою очередь, это требование можно представить в ином виде. По-скольку Фурье-образ ()xψˆ при нулевой частоте имеет вид мы мо-жем потребовать равенство нулю интеграла от вейвлета по всей оси: ()∫∞∞−,dxxψ
(1–4) ().0=∫∞∞−dxxψ15
Современная теория вейвлет-анализа в значительной степени разрабо-тана И. Добеши (Daubechies), ее работу [5, 36] можно рассматривать как об-зор для начального изучения вейвлетов.
Тенденции к росту объемов информационных массивов и повышению требований к
точности и полноте их обработки за минимальное время заставляют разработчиков новых
информационных систем наращивать их вычислительные мощности. Непрерывное
увеличение быстродействия вычислительных комплексов ведет к росту стоимости
обработки информации, далеко не всегда обеспечивая выполнение требуемых условий
обработки данных.
Таким образом, в настоящее время остается актуальной задача создания новых
методов обработки данных, которые, наряду с обеспечением заданной точности и
скорости обработки, не требовали бы обязательного увеличения мощности
вычислительных комплексов.
Широкое распространение цифровых вычислительных машин объясняется,
главным образом, универсальностью цифровых расчетов и высоким быстродействием
современных ЭВМ.
Глава I. Общие сведения
1.1. Анализ методов и требования к обработке цифровых информационных
массивов
Развитие современных универсальных ЭВМ подчинено главным образом
увеличению скорости выполнения вычислительных операций за счет увеличения тактовой
частоты центрального процессора и распараллеливания вычислительных процедур. Такое
направление развития вычислительной техники требует высокоразвитой технологической
базы, налаженного производственного процесса, а также больших материальных затрат
при создании и эксплуатации ЭВМ новых поколений. Однако даже новейшие супер-ЭВМ,
вероятнее всего, не внесут принципиальных изменений в процесс цифровой обработки
сигналов.
Эффективная обработка поступающей измерительной информации для обеспечения
оперативного решения широкого круга прикладных задач будет определяться
выполнением следующих основных требований к математическому обеспечению и
средствам обработки данных: способность перерабатывать большой объем поступающей
информации за минимальное время в условиях жестких ограничений по
энергопотреблению, массе и габаритам, обеспечивая при этом высокую
производительность вычислительных устройств и требуемую точность вычислений;
возможность распараллеливания вычислительных операций для их реализацию на ЭВМ
новых поколений; помехоустойчивость используемых алгоритмов. Кроме того,
разрабатываемые математические приемы должны обеспечивать эффективность и
устойчивость решения некорректно поставленных задач, в том числе в задачах
диагностики, анализа изображений и распознавания образов.
Рассмотрим соотношения между числовыми и аналитическими способами обработки
данных, исходя из основных требований, предъявляемых к методам обработки
информационных массивов. Под информационным (цифровым) массивом будем понимать
упорядоченную совокупность цифровых значений конечной размерности, отображающую
определенные характеристики или зависимости об изучаемом объекте или явлении.
Извлечению полезной информации из поступающих на ЭВМ информационных массивов
служат существующие и разрабатываемые вновь методы, способы и алгоритмы обработки
данных.
Проведем __________сравнительный анализ эффективности решения всего комплекса задач
существующими способами и возможными формами хранения фактографической
информации. Бурное развитие цифровой вычислительной техники в США обусловило
вполне удовлетворительное обеспечение потребителей цифровыми ЭВМ и привело к
тому, что при проведении научно-исследовательских работ цифровые расчеты стали
основным способом решения всевозможных математических задач практически во всех
областях науки и техники. Этому также в значительной степени способствовало развитое
математическое обеспечение, наличие больших программных комплексов для решения
разнообразных задач.
В нашей стране сложились другие условия. Нехватка необходимых вычислительных
мощностей, а также сложившиеся традиции русской математической школы привели к
тому, что в Советском Союзе и теперь в России основные усилия ученых и специалистов
были сосредоточены на использовании аналитических методов при решении задач. На
первом этапе уделялось большое внимание наиболее полному математическому описанию
исследуемых объектов. Затем проводились аналитические исследования, преобразования
и упрощения исходных аналитических соотношений за счет обоснованных допущений для
выявления основных свойств изучаемых объектов и явлений в целом. Такой подход
обусловил необходимость тщательного выбора математического аппарата при проведении
конкретных исследований, аккуратной и тонкой работы с аналитическими
соотношениями, продумыванию каждого последующего шага преобразований, чтобы, не
нарушая заданных условий, получить ответ, адекватно отображающий изучаемое явление
в определенном диапазоне допущений. В результате проделанной аналитической работы,
выполняемые исследования по своему научному уровню не только не уступали западным
разработкам, но и нередко далеко превосходили их достижения.
В свете сказанного рассмотрим основные достоинства и недостатки, присущие
цифровым и аналитическим методам при решении задач с использованием
вычислительной техники. При этом будем основываться как на собственном опыте, так и
на некоторых выводах, высказанных в работах других авторов (см., например, [10]).
Под аналитическими будем понимать такие решения, в которых искомая функция
F(x) выражена через независимые переменные x в виде аналитических зависимостей или
формул, бесконечных или конечных рядов или интегралов. Под численными будем
понимать решения, получаемые численно после приближенной замены исходных
уравнений другими, более простыми. Например, можно выражать производные через
конечные разности, а решение дифференциального уравнения описывать решениями
разностного уравнения. Вычисление интегралов аппроксимируется различными
формулами суммирования. Результатом указанных процедур является обычно таблица
решений при определенных значениях независимой переменной.
Основные свойства аналитических решений. К преимуществам аналитических
решений можно отнести следующие: возможность исследования влияния физических
параметров, начальных и граничных условий на характер решения; результаты
аналитических решений способствуют разработке адекватных математических моделей
исследуемых явлений, хорошо приспособлены для решения задач параметрической
идентификации и диагностики состояния исследуемых объектов; аналитические решения
более информативны, чем таблицы чисел, вычисление решения при любом конкретном
значении аргумента x можно сделать как угодно точно; возможность вычисления
значения решения в одной точке x, не прибегая к вычислению значений в других точках;
возможность определения значения искомого параметра в любой точке, а не только в
узлах сетки; устойчивость получаемого результата.
Среди недостатков аналитических решений можно назвать следующие: на практике
обычно регистрируемые информационные массивы формируются в виде числовых
таблиц, что делает невозможным непосредственное использование аналитических
преобразований в задачах обработки данных; наличие трудностей, связанных с
автоматизацией получения результата в приемлемой форме.
Основные свойства численных решений. Преимуществами численных решений
являются: универсальность, возможность получения результата в тех случаях, когда
аналитическое решение невозможно; высокое быстродействие современных цифровых
вычислительных машин, особенно при обработке целочисленных данных на ЭВМ. Из
недостатков численных решений можно выделить следующие: вычисление значения
параметра в точке и невозможность определения характера его изменений в окрестности
вычисленного значения; появление в сложных расчетах различного типа счетных
неустойчивостей, что резко снижает ценность проводимых вычислений; сложности
использования результатов расчета при создании и доводке математических моделей;
накопление в расчетах неучитываемых ошибок округления.
В основе описываемой здесь новой информационной технологии лежит принцип
реализации комбинированного численно-аналитического метода, позволяющего повысить
оперативность и достоверность обработки информационных массивов, а также
использовать преимущества, как числовых расчетов, так и аналитических преобразований
и выводов. Для включения аналитических преобразований в процесс обработки данных
необходимо на первом этапе получать с требуемой точностью аналитическое описание
цифровых массивов. Этот этап является весьма важным, так как выполненное
аналитическое описание используется в дальнейшем как исходный материал для анализа.
Выбор математического аппарата в значительной степени будет определять
эффективность аналитических выводов.
Исходя из имеющегося опыта, можно сформулировать следующие основные
требования к аналитическому описанию цифровых информационных массивов:
обеспечение заданной точности описания возможно более простым аналитическим
выражением; простота реализации на цифровых ЭВМ; возможность выполнения процедур
в автоматическом режиме; адаптивность алгоритмов аналитического описания к
особенностям каждого сигнала; унифицированность структуры описания независимо от
природы и особенностей сигнала; возможность реализации метода в условиях отсутствия
априорной информации о сигнале.
Выполнение сформулированных требований при аналитическом описании
информационных сообщений, заданных цифровыми массивами или непрерывными
кривыми, полученными в эксперименте, позволит в полной мере воспользоваться
преимуществами аналитических преобразований при решении задач обработки данных в
системах управления, навигации и распознавания образов. Учет вышесказанного
приводит к необходимости выбора подходящего метода описания и возможности
применения адаптивных процедур для достижения заданной точности наиболее простым
аналитическим выражением. Основной теоретической задачей в данном случае является
задача приближения (аппроксимации) функций, заданных числовыми массивами или
кривыми. Ее решение позволяет исследовать качественные свойства и числовые
параметры исследуемых объектов путем аналитического описания соответствующих
характеристик и их последующего изучения.
Под аппроксимацией понимают задачу нахождения для функции f(x) более простой
приближающей функции ϕ(x) из заданного класса, близкой в определенном смысле к f(x).
Теория аппроксимации в современном виде основана П.Л.Чебышевым [11]. В настоящее
время развивается теория наилучшего приближения функций алгебраическими или
тригонометрическими полиномами. Большой вклад в развитие теории полиномов
наилучшего приближения внес С.Н.Бернштейн __________и его ученики [2,3]. Наряду с
теоретическими достижениями в этой области получены и хорошие практические
результаты.
В задачах аналитического приближения функций широко применяются и другие
подходы, например, интерполяционные формулы, дающие приближенное выражение
функции f(x) посредством интерполяционного многочлена Pn(x) (Ньютона, Лагранжа и
др.) степени n. Во второй половине ХХ-го столетия существенное развитие получило
приближение так называемыми сплайн-функциями [1].
Трудности, связанные с использованием рассмотренных методов приближения для
аналитического описания значений, полученных в ходе экспериментальных исследований,
заключаются в следующем. Измерения всегда производятся с некоторой погрешностью,
поэтому для снижения влияния ошибок наблюдения увеличивают их число и
соответственно объем получаемых данных [25,26]. Задача оценки неизвестных
параметров приводит к принципу наименьших квадратов, состоящем в минимизации
функционала ∫ Σ
⎥ ⎥⎦
⎤
⎢ ⎢⎣
⎡
Φ = −
=
y x a x dx
n
i
i
i
) (, где y(x) – измеренная зависимость, Σ=
n
i
i
ai x
- ее
полиномиальное приближение, ai – искомые значения параметров. Однако метод
наименьших квадратов для приближения наблюдаемых значений аналитическими
выражениями имеет существенный недостаток. Если оказывается, что приближающий
многочлен плохо описывает измеренные значения и требуется повысить точность
описания, то для вычисления коэффициентов нового описывающего полинома более
высокой степени приходится всю процедуру повторять заново. Способ, разработанный
П.Л.Чебышевым, существенно упрощает необходимые вычисления при реализации
метода наименьших квадратов. Суть этого способа в том, что приближающий многочлен
ищется не в виде суммы степеней x, а в виде комбинации многочленов, выбранных
специальным образом. Для этого по способу наименьших квадратов [27] необходимо
искать минимум функционала
∫ () Σ ()
⎥ ⎥⎦
⎤
⎢ ⎢⎣
⎡
Φ = −
=
y x A x dx
n
i
i i
ϕ (1.1.1)
Можно показать, что вариационная задача минимизации функционала из (1.1.1)
приводит к системе уравнений, решение которой дает значения коэффициентов Ai
искомого приближающего многочлена
() () Σ=
=
n
i
y x Ai i x
ϕ (1.1.2)
где () x i
ϕ - ортогональные многочлены Чебышева, Ai - коэффициенты разложения
функции y(x) по ортогональным полиномам Чебышева. Предложенный Чебышевым
подход заключается в том, что от приближающего многочлена, в котором методом
наименьших квадратов определяются коэффициенты при степенях переменной x,
переходят к приближающему многочлену в виде суммы многочленов повышающихся
степеней (1.1.2), в котором коэффициенты при функциях () x i
ϕ также определяются
методом наименьших квадратов. В этом случае добавление новых слагаемых в (1.1.2) для
повышения точности описания не влечет изменения уже вычисленных коэффициентов Ai.
В предложенной процедуре полиномы () x i
ϕ являются взаимно ортогональными, а
коэффициенты Ai называются коэффициентами разложения функции y(x) по системе
ортогональных полиномов () x i
ϕ.
Впервые ортогональные разложения (в частном случае тригонометрических базисов)
использовались в работах Гюйгенса, Эйлера и Бернулли. Теория последних, включая
вопросы разложения по ним произвольных функций, отвечающих определенным
условиям, разработана в трудах Фурье и Вейерштрасса [12]. К настоящему времени
разработана теория многих других систем ортогональных многочленов. При этом
алгебраические ортогональные многочлены объединяются в две группы: классические
ортогональные полиномы непрерывного аргумента и классические ортогональные
полиномы дискретного аргумента [4, 13]. Указанные группы базисов объединяются целым
рядом общих признаков, которые позволяют удовлетворить сформулированные
требования по адаптивной аналитической аппроксимации экспериментальных данных.__
1–2.
Нелинейная оптимизация с ограничениями и требованием положительности переменных.(МОИ)



 H1):
H1):
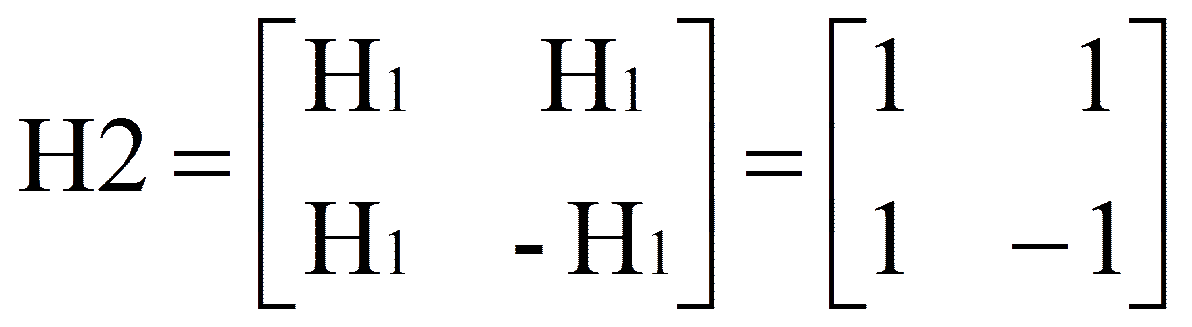 . Для N = 4 элементами матрицы Адамара будут матрицы (
. Для N = 4 элементами матрицы Адамара будут матрицы ( H2):
H2):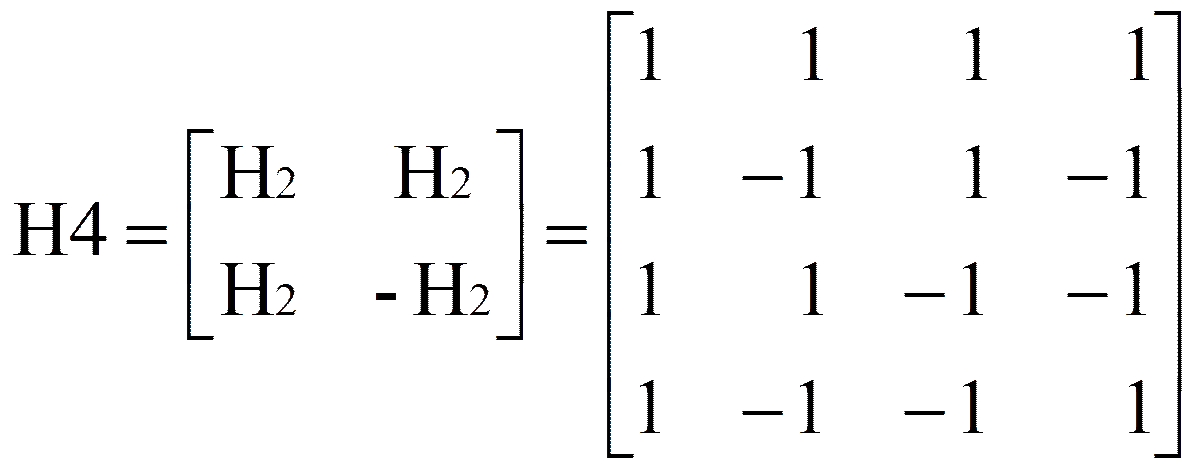 .
.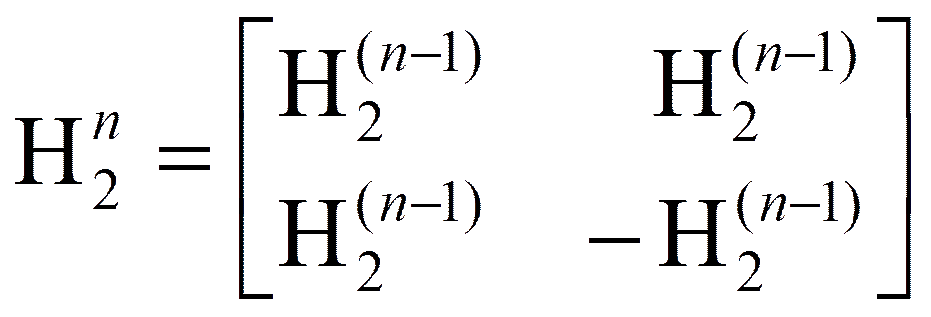 .
.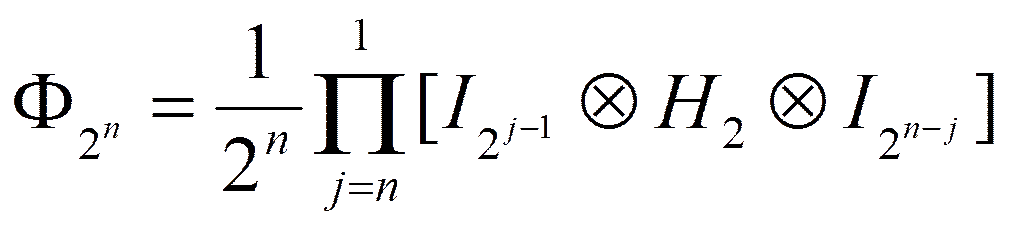 .
.


