

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
|
из
5.00
|
Заказать работу |
Доказательство: Допустим сначала, что этот предел равен конечному числу L:

Тогда по любому заданному  найдется такой номер N, что для n > N будет
найдется такой номер N, что для n > N будет
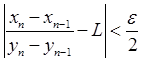
или
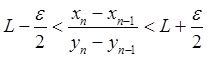 .
.
Значит, какое бы n > N ни взять, все дроби
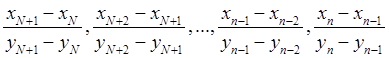
лежат между этими границами. Так как знаменатели их, ввиду возрастания уп вместе с номером п, положительны, то между теми же границами содержится и дробь
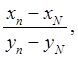
числитель которой есть сумма всех числителей, написанных выше дробей, а знаменатель – сумма всех знаменателей. Итак, при n > N
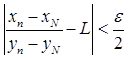
запишем тождество
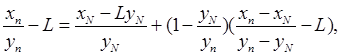
откуда
 .
.
Второе слагаемое справа, как мы видели выше, при n > N становится < 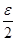 .
.
Первое же слагаемое, ввиду того, что, также будет < 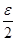 , скажем, для n > N’. Если при этом взять N’ > N, то для n > N’ очевидно
, скажем, для n > N’. Если при этом взять N’ > N, то для n > N’ очевидно
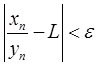 ,
,
что и доказывает наше утверждение.
Случай бесконечного предела приводится к выше рассмотренному. Пусть, например,
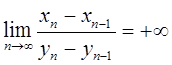
Отсюда, прежде всего, вытекает, что (для достаточно больших n)
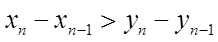
следовательно, вместе с уn и 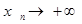 , причем варианта хп возрастает с возрастанием номера п. В таком случае, доказанную теорему можно применить к обратному отношению
, причем варианта хп возрастает с возрастанием номера п. В таком случае, доказанную теорему можно применить к обратному отношению 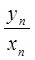 :
:
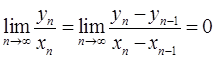
(ибо здесь предел уже конечен), откуда и следует, что
 ,
,
что и требовалось доказать.
Рассмотрим несколько примеров на применение данной теоремы
1. Вычислить 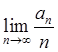
Установим одно вспомогательное неравенство (неравенство Як. Бернулли):
если п – натуральное число, большее единицы, и γ>1, то
 (*)
(*)
Действительно, положив γ =1+λ, где λ > 0, по формуле Бинома Ньютона будем иметь:
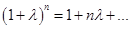
так как ненаписанные члены положительны, то
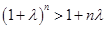 ,
,
что равносильно неравенству (*).
так же и в нашей задаче, положив а = 1+λ, так что λ > 0, имеем по формуле Бинома Ньютона
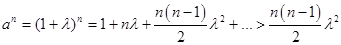 .
.
Так как для n > 2, очевидно, 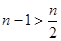 , то окончательно,
, то окончательно,
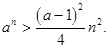
При k = 1, получаем сразу

так что
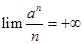
Так как этот результат верен при любом а > 1, то, взяв k > 1, можем утверждать (по крайней мере, для достаточно больших n)
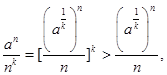
так что
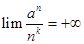 (а > 1).
(а > 1).
Доказанный, таким образом, для k = 1, этот результат тем долее будет верен и для k < 1.
Этот результат с помощью теоремы Штольца получается сразу
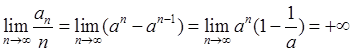
2. Применим теорему Штольца к доказательству следующего интересного предложения (Коши):
Если варианта ап имеет предел (конечный или бесконечный), то тот же предел имеет и варианта

(«среднее арифметическое» первых п значений варианты ап).
Действительно, полагая по теореме Штольца
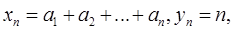
имеем:
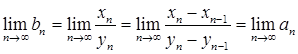
Например, если мы знаем, что 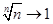 , то и
, то и
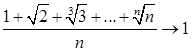
3. Рассмотрим теперь варианту (считая к – натуральным)
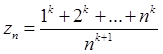 ,
,
которая представляет неопределённость вида 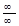 .
.
Полагая в теореме Штольца
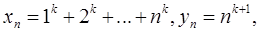
будем иметь
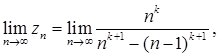
НО 
так что 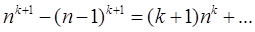
используя следующее утверждение
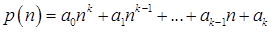
 ,
,
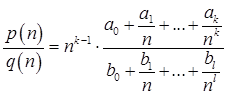
Второй множитель здесь имеет конечный предел 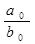 . Если степени многочленов равны k = l, то предел отношения многочленов равен пределу отношения коэффициентов при старших степенях многочленов.
. Если степени многочленов равны k = l, то предел отношения многочленов равен пределу отношения коэффициентов при старших степенях многочленов.
Если k < l, то рассматриваемое отношение стремится к 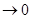
Если k > l, то рассматриваемое отношение стремится к 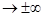
в итоге мы получаем
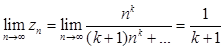
Заключение
В данной работе мы рассмотрели теорему Штольца и её применение на практике. Рассмотренные примеры показывают, что данная теорема достаточной мере облегчает процесс нахождения пределов неопределённых выражений  , помогая вычислить искомый предел, не прибегая к вспомогательным неравенствам.
, помогая вычислить искомый предел, не прибегая к вспомогательным неравенствам.
Список литературы
1. Г.М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. 1, М., 1969.
2. Б.П. Демидович, Сборник задач и упражнений по математическому анализу. М., 1977.
3. Л.Д Кудрявцев, Курс математического анализа, т. 1, М., 1988.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!