

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Рассматриваемые в этом пункте теоремы о среднем значении называют еще основными теоремами о дифференцируемых функциях.
Определение. Функция 𝑦 = 𝑓(𝑥) имеет в точке 𝑥0 локальный максимум, если существует -окрестность этой точки (𝑥0 − 𝛿; 𝑥0 + 𝛿) такая, что ∀𝑥 ∈ (𝑥0−𝛿;𝑥+𝛿): 𝑓(𝑥) < 𝑓(𝑥0).
Определение. Функция 𝑦 = 𝑓(𝑥) имеет в точке 𝑥0 локальный минимум, если существует -окрестность - (𝑥0 − 𝛿; 𝑥0 + 𝛿) такая, что ∀𝑥 ∈ (𝑥0 − 𝛿; 𝑥0 + 𝛿): 𝑓(𝑥) > 𝑓(𝑥0).
Определение. Локальные максимумы и локальные минимумы функции называются локальными экстремумами.
Локальными называются свойства функции, которые имеют место в некоторой окрестности той или другой точки.
Теорема 11.2 (теорема Ферма-1601-1665 французский математик). Пусть функция 𝑓(x) определена на интервале (𝑎; 𝑏) и в некоторой точке 𝑥0 ∈ (𝑎, 𝑏) имеет локальный экстремум. Тогда, если в точке 𝑥0 существует производная, то она равна нулю, т.е. 𝑓′(𝑥0) = 0.
Геометрический смысл теоремы Ферма состоит в том, что если в точке 𝑥0 ∈ (𝑎, 𝑏) функция имеет локальный минимум или максимум, то касательная в этой точке к графику функции 𝑦 = 𝑓(𝑥) параллельна оси 𝑂𝑥, т.е. угол наклона касательной к оси 𝑂𝑥 равен нулю, и 𝑓′(𝑥0) = tg 0 = 0.
Доказательство. По условию теоремы в точке x = 𝑥0 существует производная, но тогда можно записать, что 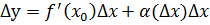 . Если
. Если 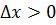 и точка
и точка 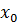 – точка максимума, то
– точка максимума, то 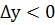 и, следовательно, из равенства для приращения функции вытекает, что производная
и, следовательно, из равенства для приращения функции вытекает, что производная 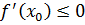 . Если же
. Если же  , то, в рассматриваемом случае, опять
, то, в рассматриваемом случае, опять 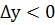 . Поэтому
. Поэтому 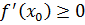 . Из полученных соотношений для производной вытекает, что единственная возможность для производной быть равной нулю
. Из полученных соотношений для производной вытекает, что единственная возможность для производной быть равной нулю  .
.
|
|
Теорема 11.3 (теорема Ролля -1652-1719 французский математик). Пусть функция 𝑓 непрерывна на отрезке [𝑎;𝑏], дифференцируема на интервале (𝑎; 𝑏) и на концах отрезка [𝑎; 𝑏] принимает равные значения, 𝑓(𝑎) =𝑓 (𝑏). Тогда существует точка 𝑐 ∈ (𝑎; 𝑏), в которой 𝑓′(𝑐) = 0.

|
Геометрически теорема Ролля означает, что  графика непрерывной на отрезке графика непрерывной на отрезке 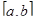 и дифференцируемой внутри этого отрезка функции, принимающей на его концах равные значения, существует точка и дифференцируемой внутри этого отрезка функции, принимающей на его концах равные значения, существует точка 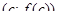 , в которой касательная параллельна оси , в которой касательная параллельна оси  . .
|
Доказательство. Так как заданная функция непрерывна на отрезке, то она достигает на нем своего наибольшего и наименьшего значений. Предположим сначала, что это происходит на концах отрезка, то есть f (a)= m = min f (x) и f (b)= M = max f (x). В такой ситуации из условий теоремы вытекает, что m = M, а это возможно только, когда функция постоянна и, следовательно, 𝑓′(𝑐) = 0, 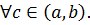 Пусть теперь наибольшее или наименьшее значение достигается внутри интервала, но тогда по теореме Ферма существует
Пусть теперь наибольшее или наименьшее значение достигается внутри интервала, но тогда по теореме Ферма существует 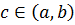 , в которой 𝑓′(𝑐) = 0 ч.т.д.
, в которой 𝑓′(𝑐) = 0 ч.т.д.
Замечание к теореме Ролля. В условиях теоремы все три условия обязательны. Рассмотрим ряд примеров.
А).  . Нарушено первое условие теоремы Ролля.
. Нарушено первое условие теоремы Ролля. 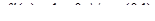 .
.
Б). 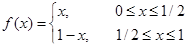 . Нарушено второе условие теоремы Ролля.
. Нарушено второе условие теоремы Ролля. 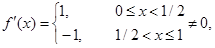 для
для  .
.
С). 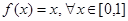 . Нарушено третье условие теоремы Ролля.
. Нарушено третье условие теоремы Ролля. 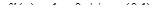 .
.
Теорема 11.4. (Лагранжа -1736-1813 французский математик). Пусть на отрезке 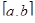 определена функция
определена функция 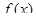 , причем:
, причем:
1) 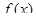 непрерывна на
непрерывна на 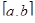 .
.
2) 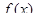 дифференцируема на
дифференцируема на 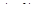 .
.
Тогда существует точка 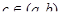 такая, что справедлива формула
такая, что справедлива формула 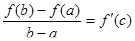 .
.
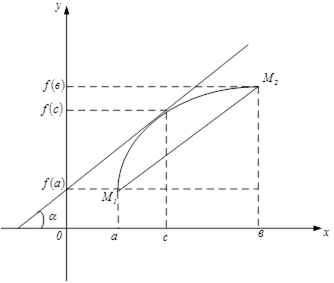
Установим геометрический смысл теоремы Лагранжа. Величина 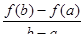 является угловым коэффициентом секущей, проходящей через точки
является угловым коэффициентом секущей, проходящей через точки 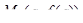 и
и 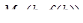 графика функции
графика функции 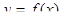 , а
, а 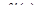 - угловой коэффициент касательной к графику в точке
- угловой коэффициент касательной к графику в точке 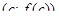 . Из теоремы Лагранжа следует, что существует такая точка
. Из теоремы Лагранжа следует, что существует такая точка 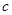 , что касательная к графику в точке
, что касательная к графику в точке 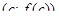 параллельна секущей
параллельна секущей 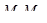 . Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
. Таких точек может быть и несколько, но, по крайней мере, одна всегда существует.
|
|
Замечание к теореме Лагранжа. Равенство  (3)
(3)
называется формулой Лагранжа или формулой конечных приращений.
Доказательство. Рассмотрим вспомогательную функцию вида
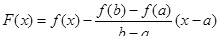 .
.
Функция  удовлетворяет всем условиям теоремы Ролля, а значит, найдется точка
удовлетворяет всем условиям теоремы Ролля, а значит, найдется точка 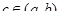 такая, что
такая, что 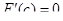 . Находим
. Находим
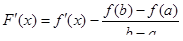 и следовательно,
и следовательно, 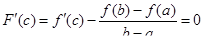 . Из последнего соотношения непосредственно следуют формулы (2) и (3). Теорема доказана.
. Из последнего соотношения непосредственно следуют формулы (2) и (3). Теорема доказана.
Следствие 1 из теоремы Лагранжа. Для того чтобы непрерывная функция  была постоянной на отрезке [ a, b ], необходимо и достаточно равенства нулю ее производной в каждой точке интервала (a, b).
была постоянной на отрезке [ a, b ], необходимо и достаточно равенства нулю ее производной в каждой точке интервала (a, b).
Доказательство. Необходимость. Пусть 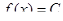 в каждой точке отрезка [ a, b ], тогда из определения производной получаем, что
в каждой точке отрезка [ a, b ], тогда из определения производной получаем, что 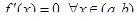 .
.
Достаточность. Пусть теперь 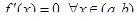 . Предположим, что
. Предположим, что 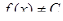 на (a, b), тогда
на (a, b), тогда 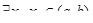 такие, что
такие, что 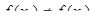 . Но по теореме Лагранжа можно записать
. Но по теореме Лагранжа можно записать 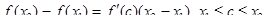 . Отсюда получаем
. Отсюда получаем 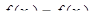 , так как по условию
, так как по условию 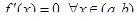 . Полученное противоречие и доказывает требуемое утверждение.
. Полученное противоречие и доказывает требуемое утверждение.
Следствие 2 из теоремы Лагранжа. Если функция  дифференцируема на интервале (а,в) и
дифференцируема на интервале (а,в) и 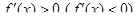 на этом интервале, то она возрастает (убывает).
на этом интервале, то она возрастает (убывает).
Доказательство. Предположим противное. Тогда найдутся точки 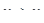 такие, что
такие, что 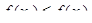 . Но по теореме Лагранжа из (3), находим
. Но по теореме Лагранжа из (3), находим
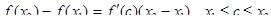 ,
,
Следовательно 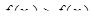 . Полученное противоречие и доказывает возрастание (убывание) функции
. Полученное противоречие и доказывает возрастание (убывание) функции  .
.
Теорема 11.5 (Коши- 1789-1857 французский математик). Пусть функция  и
и 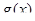 непрерывны на
непрерывны на  и дифференцируемы на
и дифференцируемы на  . Пусть
. Пусть 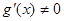 . Тогда существует точка
. Тогда существует точка 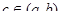 такая, что справедлива формула
такая, что справедлива формула
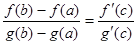
Эта формула называется формулой Коши или обобщенной формулой конечных приращений.
Доказательство. Рассмотрим вспомогательную функцию вида
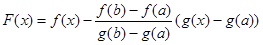 . Заметим, что
. Заметим, что  , так как в противном случае функция
, так как в противном случае функция 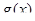 удовлетворяла бы условиям теоремы Ролля и тогда, нашлась бы точка
удовлетворяла бы условиям теоремы Ролля и тогда, нашлась бы точка 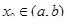 , в которой
, в которой  , что противоречит условию теоремы. Таким образом, функция
, что противоречит условию теоремы. Таким образом, функция  определена на [ a, b ] и удовлетворяет всем условиям теоремы Ролля. Поэтому
определена на [ a, b ] и удовлетворяет всем условиям теоремы Ролля. Поэтому
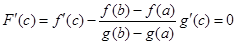 . Последнее равенство и доказывает справедливость формулы (4). Теорема доказана.
. Последнее равенство и доказывает справедливость формулы (4). Теорема доказана.
Теорема 11.6. (Лопиталя 1661 – 1704 французский математик). Пусть функции  и
и 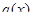 дифференцируемы во всех точках некоторой окрестности точки
дифференцируемы во всех точках некоторой окрестности точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  . Пусть
. Пусть 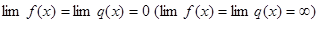 и
и 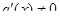 во всех точках этой окрестности. Тогда, если существует (конечный или бесконечный) предел
во всех точках этой окрестности. Тогда, если существует (конечный или бесконечный) предел 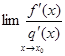 , то существует
, то существует 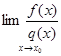 , причем
, причем
|
|
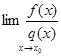

Доказательство. Доопределим функции  и
и 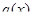 в точке
в точке  , положив
, положив 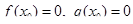 . Рассмотрим отрезок
. Рассмотрим отрезок 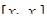 . Заданные функции удовлетворяют всем условиям теоремы Коши. Поэтому
. Заданные функции удовлетворяют всем условиям теоремы Коши. Поэтому
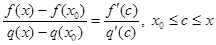 .
.
Переходя в последнем равенстве к пределу при 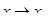 и учитывая, что при этом
и учитывая, что при этом  , получаем требуемое выражение. Если
, получаем требуемое выражение. Если 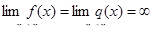 , то зафиксируем точку
, то зафиксируем точку 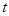 из окрестности точки
из окрестности точки  . Пусть
. Пусть 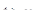 . Рассмотрим отрезок
. Рассмотрим отрезок 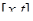 . В этом отрезке функции
. В этом отрезке функции  и
и 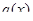 удовлетворяют теореме Коши. Поэтому
удовлетворяют теореме Коши. Поэтому
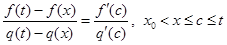 . Перепишем это равенство в следующем виде
. Перепишем это равенство в следующем виде
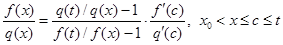 .
.
Переходя к пределу при 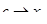 и учитывая, что при этом
и учитывая, что при этом 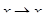 , получаем опять равенство необходимое равенство. Теорема доказана.
, получаем опять равенство необходимое равенство. Теорема доказана.
Эта теорема дает правило для раскрытия неопределенности вида 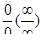 , сводящее вычисление предела отношения двух функций к вычислению предела отношения их производных.
, сводящее вычисление предела отношения двух функций к вычислению предела отношения их производных.
11.7. Формула Тейлора (Английский математик, 1685-1731 гг.)
Пусть функция  определена и (n +1) раз дифференцируема в окрестности некоторой точки a. Составим выражение
определена и (n +1) раз дифференцируема в окрестности некоторой точки a. Составим выражение
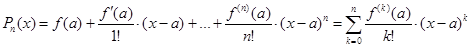 .
.
Обозначим 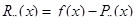 . Тогда можно записать
. Тогда можно записать
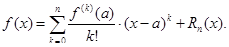
Формула (10) называется формулой Тейлора, а функция 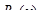 - остаточным членом в формуле Тейлора.
- остаточным членом в формуле Тейлора.
Используя теорему Коши нетрудно получить выражение для остаточного члена. Действительно, рассмотрим функции 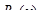 и
и 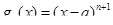 . Очевидно, что
. Очевидно, что
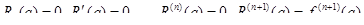 и
и
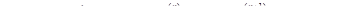
Применяя (n+1) раз теорему Коши на отрезке [ a, x ] для функций 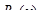 и
и  , находим
, находим
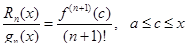 или
или
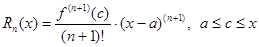
Выражение для 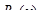 принято называть остаточным членом формулы Тейлора в форме Лагранжа.
принято называть остаточным членом формулы Тейлора в форме Лагранжа.
Формула Тейлора широко применяется для обоснования различных положений при исследовании функций.
|
|
|

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!