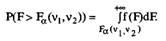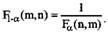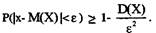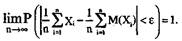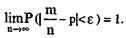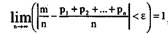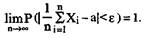1. х2 -распределение Пирсона. Пусть X1, X2,...,Хn одинаково распределенные по нормальному закону случайные величины, являющиеся взаимно-независимыми, для которых математическое ожидание равно нулю, а среднеквадратическое отклонение 1, тогда сумма квадратов этих случайных величин носит название случайной величины х2 - xu-квадрат с v=n степенями свободы:

При v=l (учитывая дифференциальная функция:
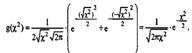
Дифференциальная функция распределения χ2 с v=n степенями свободы задается формулой
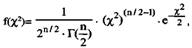
где Г(х) - гамма, функция Эйлера.
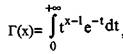
при R+; если n Z, то Г(n+ 1)=n!
С возрастанием числа степеней свободы v = n, распределение χ2 медленно приближается к нормальному закону распределения. На практике используют обычно не плотность вероятности, а квантили распределения.
Квантилью χ2n распределения, отвечающей заданному уровню значимости α (альфа) – χ2α,ν, называется такое значение χ2= χ2α,ν, при котором вероятность того, что χ2 превысит значение χ2α,ν, равна α (рис.21):
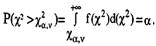
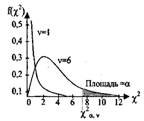
Рис. 21. Дифференциальная функция распределения χ 2 с ν степенями свободы.
С геометрической точки зрения нахождение квантили
заключается в выборе такого значения Х2= 5Ca v при котором площадь криволинейной трапеции ограниченной дифференциальной функцией была бы равна а. Значения квантилей затабулированы (прил.2). При n>30 распределение практически не отличается от нормального.
Замечание. Квантиль СВ X порядка a - это такое значение СВ X, что F(xa) = а, где F(x)=P(X<x). Например, медиана – это квантиль x0.5.
2. t- распределение Стъюдента. Это распределение имеет важное значение при статистических вычислениях, связанных с нормальным законом, распределения, где a - неизвестный параметр распределения и подлежит
определению из опытных данных, например, при статистической обработке наблюдений с неизвестной точностью.
Пусть X, X,, X2,...,Xk независимые нормально распределённые случайные величины с нулевыми математическими ожиданиями и одинаковыми дисперсиями. Безразмерная величина
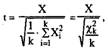
называется дробью Стьюдента.
Ее распределение не зависит от а в силу ее безразмерности. Дифференциальная функция t-распределения с v=k степенями свободы имеет вид
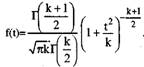
t - распределение Стьюдента быстрее, чем х2 стремится к нормальному.
На практике используют квантили распределения в зависимости от числа степеней свободы и уровня значимости α.
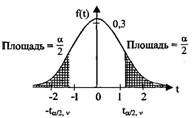
С геометрической точки зрения нахождение квантилей (для двусторонней области) заключается в выборе такого значения t, при котором суммарная площадь криволинейной трапеции была бы равна α, в силу симметрии распределения (рис. 22):
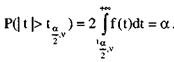
Рис.22. Дифференциальная функция t-распределения Стьюдента с v=k≤30 степенями свободы.
 3. F-распределение Фишера-Снедекора.
3. F-распределение Фишера-Снедекора.
Пусть Х1, X2,...,Xm и Y1, Y2,...,Yn одинаково распределенные по нормальному закону случайные величины, являющиеся взаимно-независимыми, для которых математическое ожидание равно нулю, а среднеквадратическое отклонение равно единице.
Рассмотрим дробь Фишера F(m,n)=(χ2m/m)/(χ2n/n), она имеет F - распределение с v1 = m - числом степеней свободы числителя, и v2=n - числом степеней свободы знаменателя ((m, n) степенями свободы), которое называется распределением Фишера-Снедекора. Обычно используют квантили распределения в зависимости от числа степеней свободы (m, n) и уровня значимости а. (рис. 23):
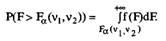
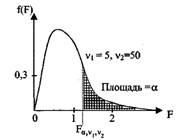
Рис. 23. Дифференциальная функция F распределения Фишера -Снедекора с v1=5, v2=50 степенями свободы
Для квантилей распределения Фишера-Снедекора геометрический смысл аналогичен другим распределениям (рис.23). Имеет место равенство
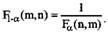
Распределения χ2 - Пирсона, t - Стьюдента, F -Фишера-Снедекора нашли широкое применение в математической статистике, в частности при проверке статистических гипотез и в дисперсионном анализе.
Закон больших чисел
Под законом больших чисел в теории вероятностей понимают совокупность теорем, в которых утверждается, что существует связь между средним арифметическим достаточно большого числа случайных величин и средним арифметическим их математических ожиданий.
В1927 г. Гейзенберг открыл принцип неопределенности, который утверждает, что измерительное познание ограничено. Неопределенность является неотъемлемой частью нашей жизни, однако, при большом числе однотипных опытов можно установить определенные закономерности.
Неравенство Чебышева.
Рассмотрим закон больших чисел в форме Чебышева.
Лемма Чебышева (Маркова). Если случайная величина X принимает только неотрицательные значения и имеет математическое ожидание М(Х), то для любого α>0 имеет место неравенство: P(X≥α)≤(M(X))/α.
Неравенство Чебышева. Если случайная величина X имеет математическое ожидание М(Х) и дисперсию D(X), то для любого ε>0 имеет место неравенство:
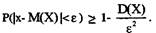
Неравенство Чебышева является в теории вероятностей общим фактом и позволяет оценить нижнюю границу вероятности.
30. Теорема. Закон больших чисел Чебышева. Пусть Х1, Х2,...,Хn - последовательность попарно независимых случайных величин, имеющих конечные математические ожидания и дисперсии, ограниченные сверху постоянной С = const (D(Xi)≤C(i=l, 2,...,n)). Тогда для любого ε>0,
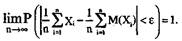
Теорема показывает, что среднее арифметическое большого числа случайных величин с вероятностью сколь угодно близкой к 1 будет мало отклоняться от среднего арифметического математических ожиданий.
Следствие 1. Если вероятность наступления события А в каждом из n независимых испытаний равна р, m - число наступлений события А в серии из n независимых испытаний, то, каково бы ни было число е > 0, имеет место предел: 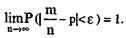
Таким образом устанавливается связь между относительной частотой появления события А и постоянной вероятностью р в серии из n независимых испытаний.
Следствие 2. Теорема Пуассона. Если в последовательности независимых испытаний вероятность появления события А в к-ом испытании равна р, то
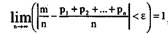
где m - число появлений события А в серии из n испытаний.
Следствие 3. Теорема Бернулли. Если X1, Х2,...,Хn - последовательность независимых случайных величин таких, что М(Х1) = М(Х2)=...= М(Хn) = а, D(Х1)< С, D(X2) < С,...,D(Xn)< С, где С = const, то, каково бы ни было постоянное число ε>0, имеет место предел:
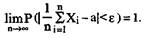
Этот частный случай закона больших чисел позволяет обосновать правило средней арифметической.
Законы больших чисел не позволяют уменьшить неопределённость в каждом конкретном случае, они утверждают лишь о существовании закономерности при достаточно большом числе опытов. Например, если при подбрасывании монеты 10 раз появился герб, то это не означает, что в 11 раз появится цифра.





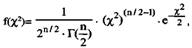
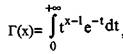
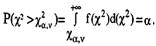

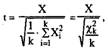
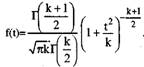
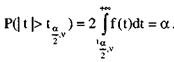
 3. F-распределение Фишера-Снедекора.
3. F-распределение Фишера-Снедекора.