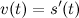Если  и
и  строго возрастает на
строго возрастает на 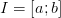 , то на
, то на  определена функция
определена функция 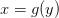 , которая будет обратная к
, которая будет обратная к  , непрерывна на
, непрерывна на 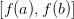 и будет строго возрастать на
и будет строго возрастать на 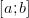 .
.
Если  и
и  строго убывает на
строго убывает на 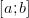 , то на
, то на 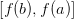 определена функция
определена функция 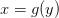 , которая будет обратная к
, которая будет обратная к  , непрерывна на
, непрерывна на 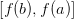 и будет строго убывать на
и будет строго убывать на 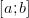 .
.
Доказательство:
Предположим, что функция  строго возрастает на отрезке
строго возрастает на отрезке 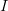 .
.
По следствию из 2-ой теоремы Коши о промежуточном значении непрерывных функций область значений 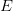 непрерывной функции
непрерывной функции  тоже есть отрезок.
тоже есть отрезок.
В силу строгого возрастания функции  для каждого
для каждого 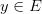 существует единственная точка
существует единственная точка 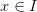 такая, что
такая, что 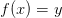 .
.
Следовательно для функции  существует обратная функция
существует обратная функция 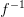 определенная на отрезке
определенная на отрезке 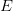 и с множеством значений
и с множеством значений 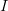 .
.
Покажем, что 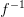 строго возрастает на
строго возрастает на 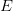 .
.
Пусть 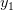 и
и 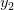 – две произвольные точки из
– две произвольные точки из 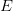 , такие, что
, такие, что 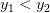 и прообразами этих точек будут точки
и прообразами этих точек будут точки  и
и 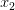 .
. 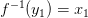 и
и 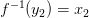 .
.
Поскольку  – строго возрастающая функция, то неравенство
– строго возрастающая функция, то неравенство 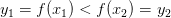 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 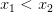 или, что то же самое, когда
или, что то же самое, когда 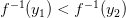 .
.
В силу произвольности 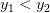 делаем вывод, что функция
делаем вывод, что функция 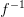 – строго возрастает на множестве
– строго возрастает на множестве 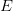 .
.
Для случая, когда  строго убывает теорема доказывается аналогично.
строго убывает теорема доказывается аналогично.
Билет №20. Непрерывность основных элементарных ф-й.
Утверждение 1
Рассмотрим многочлен степени 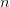 , т. е. функцию вида
, т. е. функцию вида
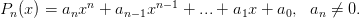
Эта функция непрерывна на 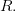
Рациональная функция, т. е. функция вида 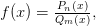 где
где 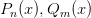 — многочлены степени
— многочлены степени 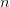 и
и 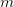 соответственно, непрерывна во всех точках, которые не являются нулями многочлена
соответственно, непрерывна во всех точках, которые не являются нулями многочлена 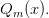
Утверждение 2
Если 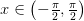 и
и 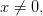 то
то 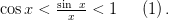
Следствие
Первый замечательный предел

Утверждение 3
Для всех 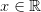 справедливо неравенство
справедливо неравенство
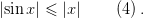
Утверждение 4
Функции 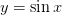 и
и 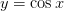 непрерывны на всем множестве
непрерывны на всем множестве 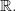
Следствие
Функция 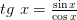 – непрерывная при
– непрерывная при 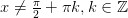
Утверждение 5
Рассмотрим несколько функции с их графиками
1. 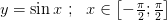 строго возрастает и непрерывна
строго возрастает и непрерывна
2. 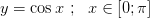 строго спадает и непрерывна
строго спадает и непрерывна
3. 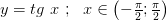 строго возрастает и непрерывна
строго возрастает и непрерывна
4. 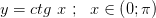 строго спадает и непрерывна
строго спадает и непрерывна
Тогда по теореме существуют обратные непрерывные монотонные функции соответственно
1. 
2. 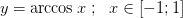
3. 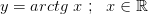
4. 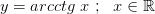
Утверждение 6
Функция 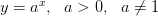 – монотонна непрерывна на
– монотонна непрерывна на 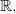 то есть
то есть
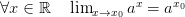
и тогда функция 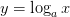 – монотонна и непрерывна(как обратная)
– монотонна и непрерывна(как обратная)
Утверждение 7
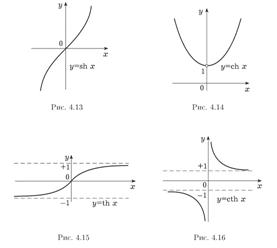
Функции, заданные формулами

называют соответственно гиперболическим синусом и гиперболическим косинусом.
Эти функции определены и непрерывны на 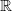 , причем
, причем 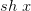 — нечетная функция, а
— нечетная функция, а 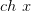 – четная функция.
– четная функция.
Из определения функций 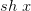 и
и 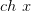 следует, что
следует, что

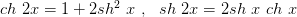
По аналогии с тригонометрическими функциями гиперболические тангенс и котангенс определяются соответственно формулами
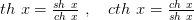
Функция 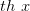 определена и непрерывна на
определена и непрерывна на 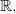 а функция
а функция  определена и непрерывна на множестве
определена и непрерывна на множестве 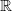 с выколотой точкой
с выколотой точкой 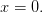 Обе функции нечетные.
Обе функции нечетные.
Утверждение 8
Пусть функции 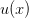 и
и 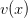 определены на промежутке
определены на промежутке 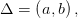 причем для всех
причем для всех 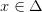 выполняется условие
выполняется условие  Тогда функцию
Тогда функцию 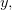 определяемую формулой
определяемую формулой
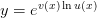
будем называть показательно-степенной и обозначать
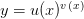
Таким образом, исходя из определения
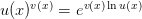
Если 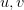 — функции, непрерывные на
— функции, непрерывные на 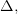 то функция
то функция 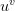 непрерывна на
непрерывна на 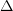 как суперпозиция непрерывных функций
как суперпозиция непрерывных функций 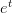 и
и 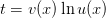 .
.
Билет №21. Обратные тригонометрические функции и их свойства.
Функция arcsin


График функции 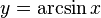 .
.
Арксинусом числа m называется такое значение угла x, для которого 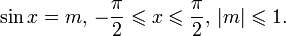
Функция 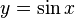 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 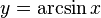 является строго возрастающей.
является строго возрастающей.
· 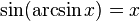 при
при 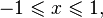
· 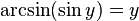 при
при 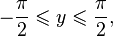
· 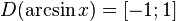 (область определения),
(область определения),
· 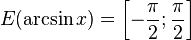 (область значений).
(область значений).
]Свойства функции arcsin
· 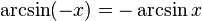 (функция является нечётной).
(функция является нечётной).
· 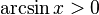 при
при 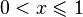 .
.
· 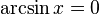 при
при 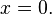
· 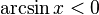 при
при 
· 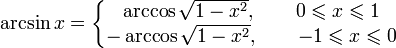
· 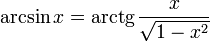
· 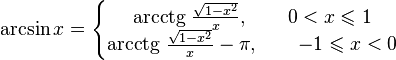
Функция arccos
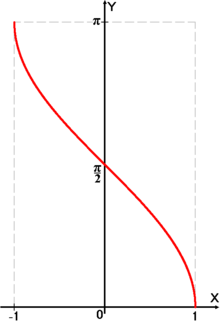

График функции 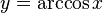 .
.
Арккосинусом числа m называется такое значение угла x, для которого 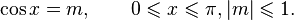
Функция 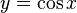 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 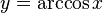 является строго убывающей.
является строго убывающей.
· 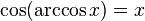 при
при 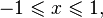
· 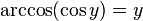 при
при 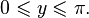
· 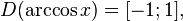 (область определения),
(область определения),
· 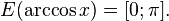 (область значений).
(область значений).
[править]Свойства функции arccos
· 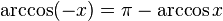 (функция центрально-симметрична относительно точки
(функция центрально-симметрична относительно точки 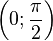 ), является индифферентной.
), является индифферентной.
· 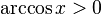 при
при 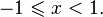
·  при
при 
· 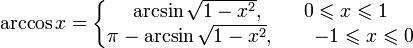
· 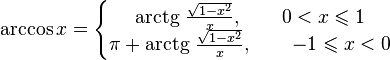
· 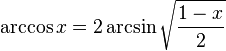
· 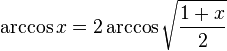
· 
Функция arctg
График функции 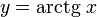 .
.
Арктангенсом числа m называется такое значение угла 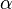 , для которого
, для которого 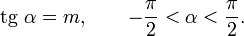
Функция 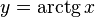 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 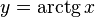 является строго возрастающей.
является строго возрастающей.
· 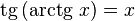 при
при 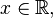
· 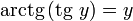 при
при 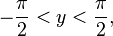
· 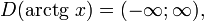
· 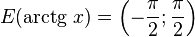
Свойства функции arctg
· 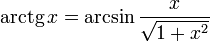
· 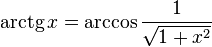 , при x > 0.
, при x > 0.
·  , при x > 0.
, при x > 0.
Функция arcctg
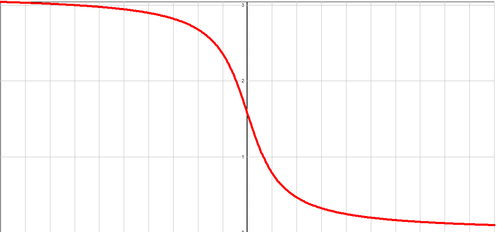

График функции y=arcctg x
Арккотангенсом числа m называется такое значение угла x, для которого 
Функция 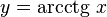 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 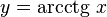 является строго убывающей.
является строго убывающей.
· 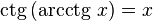 при
при 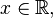
·  при
при 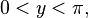
· 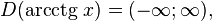
· 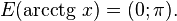
]Свойства функции arcctg
· 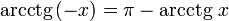 (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 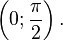
· 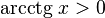 при любых
при любых 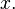
· 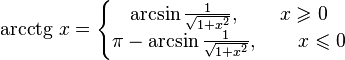
Билет №22. Гиперболические ф-и и их сво-ва.

Билет №23. Определение производной, ее геометрический и механический смысл. Ур-е касательной и нормали к гр ф-и. односторонние и бесконечные производные.


(Механический смысл производной)
Пусть задан путь 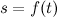 движения материальной точки. Скорость данной материальной точки в момент времени
движения материальной точки. Скорость данной материальной точки в момент времени 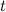 есть производная от пути
есть производная от пути  по времени
по времени 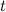 :
:
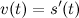



 и
и  строго возрастает на
строго возрастает на 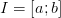 , то на
, то на  определена функция
определена функция 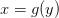 , которая будет обратная к
, которая будет обратная к 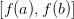 и будет строго возрастать на
и будет строго возрастать на 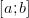 .
.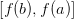 определена функция
определена функция 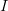 .
.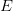 непрерывной функции
непрерывной функции 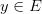 существует единственная точка
существует единственная точка 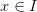 такая, что
такая, что 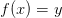 .
.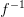 определенная на отрезке
определенная на отрезке 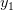 и
и 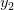 – две произвольные точки из
– две произвольные точки из 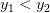 и прообразами этих точек будут точки
и прообразами этих точек будут точки  и
и 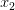 .
. 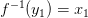 и
и 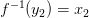 .
.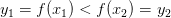 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда 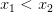 или, что то же самое, когда
или, что то же самое, когда 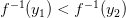 .
.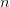 , т. е. функцию вида
, т. е. функцию вида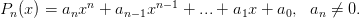
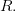
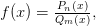 где
где 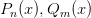 — многочлены степени
— многочлены степени 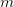 соответственно, непрерывна во всех точках, которые не являются нулями многочлена
соответственно, непрерывна во всех точках, которые не являются нулями многочлена 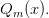
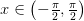 и
и 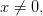 то
то 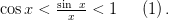

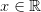 справедливо неравенство
справедливо неравенство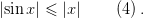
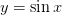 и
и 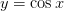 непрерывны на всем множестве
непрерывны на всем множестве 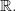
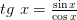 – непрерывная при
– непрерывная при 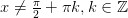
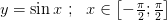 строго возрастает и непрерывна
строго возрастает и непрерывна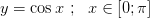 строго спадает и непрерывна
строго спадает и непрерывна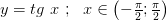 строго возрастает и непрерывна
строго возрастает и непрерывна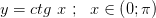 строго спадает и непрерывна
строго спадает и непрерывна
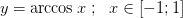
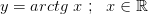
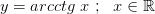
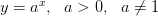 – монотонна непрерывна на
– монотонна непрерывна на 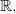 то есть
то есть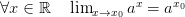
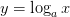 – монотонна и непрерывна(как обратная)
– монотонна и непрерывна(как обратная)
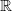 , причем
, причем 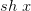 — нечетная функция, а
— нечетная функция, а 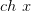 – четная функция.
– четная функция.
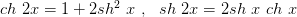
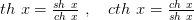
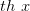 определена и непрерывна на
определена и непрерывна на  определена и непрерывна на множестве
определена и непрерывна на множестве 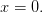 Обе функции нечетные.
Обе функции нечетные.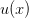 и
и 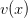 определены на промежутке
определены на промежутке 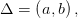 причем для всех
причем для всех 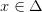 выполняется условие
выполняется условие  Тогда функцию
Тогда функцию 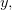 определяемую формулой
определяемую формулой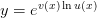
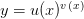
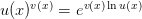
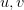 — функции, непрерывные на
— функции, непрерывные на 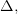 то функция
то функция 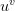 непрерывна на
непрерывна на 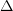 как суперпозиция непрерывных функций
как суперпозиция непрерывных функций 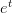 и
и 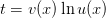 .
.

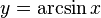 .
.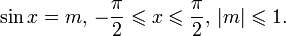
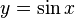 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 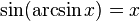 при
при 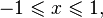
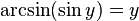 при
при 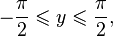
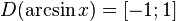 (область определения),
(область определения),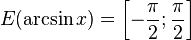 (область значений).
(область значений).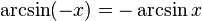 (функция является нечётной).
(функция является нечётной).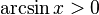 при
при 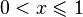 .
.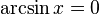 при
при 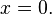
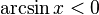 при
при 
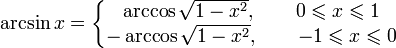
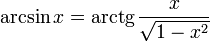
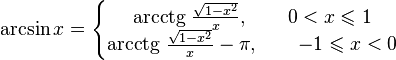

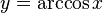 .
.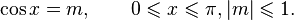
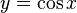 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 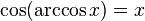 при
при 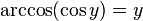 при
при 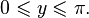
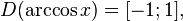 (область определения),
(область определения),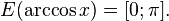 (область значений).
(область значений).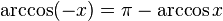 (функция центрально-симметрична относительно точки
(функция центрально-симметрична относительно точки 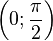 ), является индифферентной.
), является индифферентной.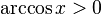 при
при 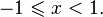
 при
при 
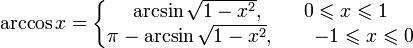
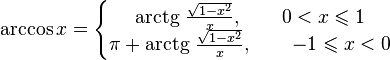
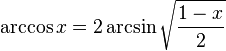
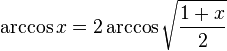

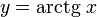 .
.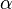 , для которого
, для которого 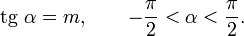
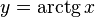 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 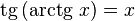 при
при 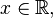
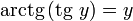 при
при 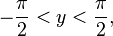
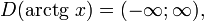
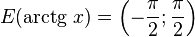
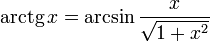
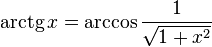 , при x > 0.
, при x > 0. , при x > 0.
, при x > 0.

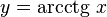 непрерывна и ограничена на всей своей числовой прямой. Функция
непрерывна и ограничена на всей своей числовой прямой. Функция 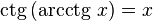 при
при  при
при 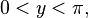
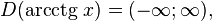
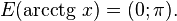
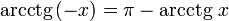 (график функции центрально-симметричен относительно точки
(график функции центрально-симметричен относительно точки 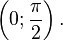
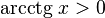 при любых
при любых 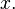
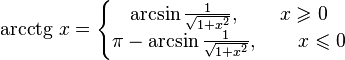




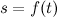 движения материальной точки. Скорость данной материальной точки в момент времени
движения материальной точки. Скорость данной материальной точки в момент времени 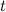 есть производная от пути
есть производная от пути  по времени
по времени