1° 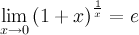
2° 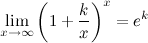
3° 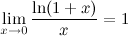
4° 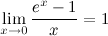
5° 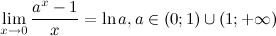
6° 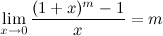
Билет №13. Сравнение бмфун-й. Св-ва эквивалентных бмфу-й.
Функция 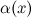 называется бесконечно малой функцией (б.м.ф.) при
называется бесконечно малой функцией (б.м.ф.) при 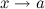 (или в точке
(или в точке 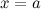 ), если
), если 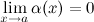
Функции 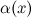 и
и 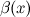 называются б.м. одного порядка малости при
называются б.м. одного порядка малости при 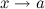 , если
, если 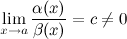
Если 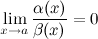 , то
, то 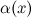 является б.м. более высокого порядка при
является б.м. более высокого порядка при 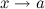 , чем
, чем 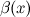 , а
, а 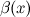 - б.м. более низкого порядка по сравнению с
- б.м. более низкого порядка по сравнению с 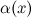 :
: 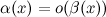 при
при 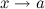 .
.
Если 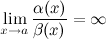 , то
, то 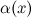 - б.м. низшего порядка малости при
- б.м. низшего порядка малости при 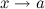 по сравнению с
по сравнению с 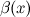 .
.
Если 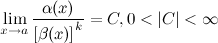 , то
, то 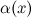 называется б.м. порядка
называется б.м. порядка 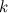 по сравнению с
по сравнению с 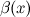 при
при 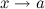 .
.
Если 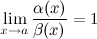 , то б.м. функции
, то б.м. функции 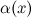 и
и 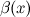 называются эквивалентными или равносильными б.м. одного порядка при
называются эквивалентными или равносильными б.м. одного порядка при 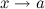 :
: 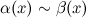 при
при 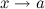 .
.
Таблица эквивалентных б.м. функций при 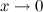
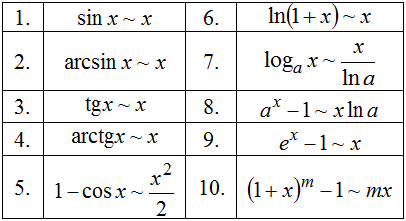
Свойства:
· Предел отношения двух б.м. функций 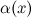 и
и 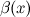 при
при 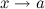 равен пределу отношения эквивалентных им б.м. функций
равен пределу отношения эквивалентных им б.м. функций 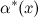 и
и  при
при 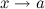 , то есть верны предельные равенства:
, то есть верны предельные равенства:
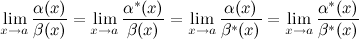
· Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них. Верно и обратное утверждение.
· Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.
Билет №14. Определение непрерывности ф-ции в точке. Классификация точек разрыва.
Функция  называется непрерывной в точке
называется непрерывной в точке  , если:
, если:
1. функция  определена в точке
определена в точке  и ее окрестности;
и ее окрестности;
2. существует конечный предел функции  в точке
в точке  ;
;
3. это предел равен значению функции в точке  , т.е.
, т.е. 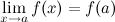
Точка  , в которой нарушено хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции.
, в которой нарушено хотя бы одно из трех условий непрерывности функции, называется точкой разрыва функции.
Классификация точек разрыва:
Если в точке  существуют конечные пределы
существуют конечные пределы 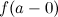 и
и 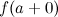 , такие, что
, такие, что 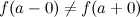 , то точка
, то точка  называется точкой разрыва первого рода.
называется точкой разрыва первого рода.
Если хотя б один из пределов 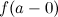 или
или 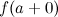 не существует или равен бесконечности, то точка
не существует или равен бесконечности, то точка  называется точкой разрыва второго рода.
называется точкой разрыва второго рода.
Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции  в точке
в точке  :
: 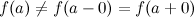 или функция
или функция  не определена в точке
не определена в точке  , то точка
, то точка  называется точкой устранимого разрыва.
называется точкой устранимого разрыва.
Билет №15. Непрерывность ф-ции в точке(Б-14). Св-ва ф-ций, непрерывных в точке.
С-ва:
1. Функция  непрерывна в точке
непрерывна в точке  тогда и только тогда, когда бесконечно малому приращению аргумента
тогда и только тогда, когда бесконечно малому приращению аргумента 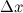 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 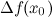 :
:
2. 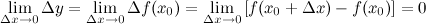
3. Если функции  и
и 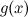 непрерывны в точке
непрерывны в точке  , то функции
, то функции 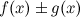 ,
, 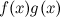 ,
, 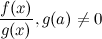 также непрерывны в точке
также непрерывны в точке  .
.
4. Пусть функция 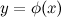 непрерывна в точке
непрерывна в точке  , а функция
, а функция 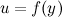 непрерывна в точке
непрерывна в точке 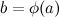 . Тогда композиция функций
. Тогда композиция функций 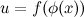 непрерывна в точке
непрерывна в точке  .
.
5. Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.
Билет №16. Непрерывность фу-и на отрезке. Теоремы об ограниченности и достижении точкой нижней и верхних граней ф-ии непрерывной на отрезке.
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Функция  называется непрерывной справа в точке
называется непрерывной справа в точке  , если
, если 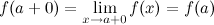 .
.
Функция  называется непрерывной слева в точке
называется непрерывной слева в точке  , если
, если 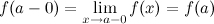 .
.
Функция 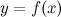 называется непрерывной в интервале
называется непрерывной в интервале 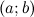 , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала.
Функция 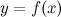 называется непрерывной на отрезке
называется непрерывной на отрезке 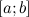 , если она является непрерывной в интервале
, если она является непрерывной в интервале 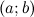 , непрерывной справа в точке
, непрерывной справа в точке  , то есть
, то есть 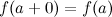 и непрерывной слева в точке
и непрерывной слева в точке 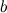 , то есть
, то есть 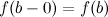 .
.
Свойства функций непрерывных на отрезке:
1. Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.
2. Непрерывная на отрезке 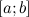 функция является ограниченной на этом отрезке.
функция является ограниченной на этом отрезке.
3. Теорема Больцано-Коши. Если функция 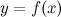 является непрерывной на отрезке
является непрерывной на отрезке 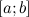 и принимает на концах этого отрезка неравные между собой значения, то есть
и принимает на концах этого отрезка неравные между собой значения, то есть 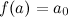 ,
, 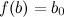 , то на этом отрезке функция принимает и все промежуточные значения между
, то на этом отрезке функция принимает и все промежуточные значения между 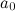 и
и 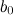 .
.
4. Если функция 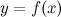 , которая непрерывна на некотором отрезке
, которая непрерывна на некотором отрезке 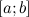 , принимает на концах отрезка значения разных знаков, то существует такая точка
, принимает на концах отрезка значения разных знаков, то существует такая точка 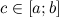 такая, что
такая, что 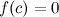 .
.
Билет №17. Непрерывность фу-и на отрезке (Б-16). Теоремы о нулях и о промежуточных значениях ф-ии, непрерывной на отрезке.



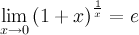
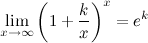
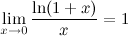
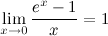
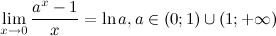
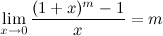
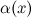 называется бесконечно малой функцией (б.м.ф.) при
называется бесконечно малой функцией (б.м.ф.) при 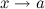 (или в точке
(или в точке 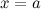 ), если
), если 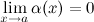
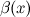 называются б.м. одного порядка малости при
называются б.м. одного порядка малости при 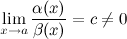
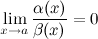 , то
, то 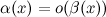 при
при 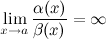 , то
, то 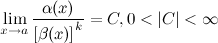 , то
, то 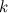 по сравнению с
по сравнению с 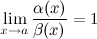 , то б.м. функции
, то б.м. функции 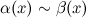 при
при 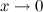
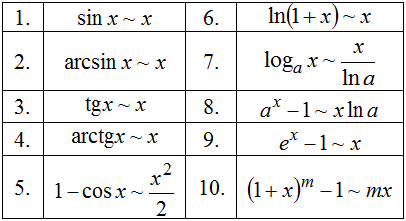
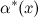 и
и  при
при 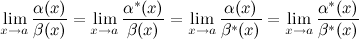
 называется непрерывной в точке
называется непрерывной в точке  , если:
, если: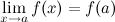
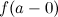 и
и 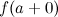 , такие, что
, такие, что 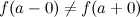 , то точка
, то точка 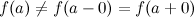 или функция
или функция 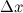 соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции 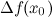 :
: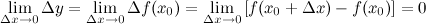
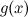 непрерывны в точке
непрерывны в точке 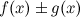 ,
, 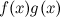 ,
, 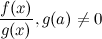 также непрерывны в точке
также непрерывны в точке 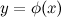 непрерывна в точке
непрерывна в точке 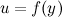 непрерывна в точке
непрерывна в точке 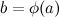 . Тогда композиция функций
. Тогда композиция функций 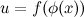 непрерывна в точке
непрерывна в точке 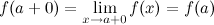 .
.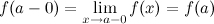 .
.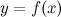 называется непрерывной в интервале
называется непрерывной в интервале 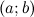 , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала.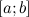 , если она является непрерывной в интервале
, если она является непрерывной в интервале 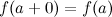 и непрерывной слева в точке
и непрерывной слева в точке 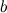 , то есть
, то есть 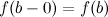 .
.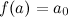 ,
, 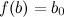 , то на этом отрезке функция принимает и все промежуточные значения между
, то на этом отрезке функция принимает и все промежуточные значения между 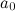 и
и 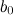 .
.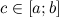 такая, что
такая, что 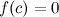 .
.


