Стратегии в дискретной игре с открытой информацией

 

Как пример применения понятий графа и дерева рассмотрим дискретную игру двух лиц А и В с открытой информацией.

Игра двух лиц с открытой информацией представляет собой:

– множество ситуаций Н = { H_i } (среди них – начальная ситуация Н₀);

– правила игры – порождающая процедура, определяющая возможные переходы из одной ситуации в другую: для каждой ситуации Н_i определено множество Т_i ={ } ситуаций, в которые можно перейти ходом одного из игроков;

– для некоторых ситуаций Н_j множество Т_j пустое – такие ситуации называются заклю-чительными; каждой из них приписан один из символов А или В, называемых результатом игры (возможен вариант – один из трех символов: А, В, 0).

Партия (тур) игры состоит в том, что игроки по очереди (будем считать, что первый ход принадлежит игроку А) делают допустимые правилами ходы и, начиная с ситуации Н₀, переводят игру в очередную ситуацию. При попадании в любую заключительную ситуацию игра заканчивается, и результат определяет, какой из игроков – А или В – выиграл в этой партии (результат 0, если он является допустимым, означает ничью).

Дискретная игра может быть представлена ориентированным графом { H, T }: H – множество вершин, T (Н_i) задает множество дуг, исходящих из Н_i. Партия (тур) представляет собой траекторию с началом в Н₀ и концом в одном из заключительных состояний; однако возможен вариант, когда партия бесконечна, если, например, в графе имеется контур. В дальнейшем будем рассматривать только конечные игры.

Примером конечной игры (с возможностью ничейного исхода) являются шахматы. Правила шахматной игры определяют допустимые ходы и обеспечивают конечность игры: ничья после троекратного повторения позиции, а также после 50 ходов без взятий фигур, превращений и ходов пешек.

Отметим, кстати, что позиция фигур на шахматной доске (даже с указанием очередности хода) не определяет, вообще говоря, ситуации полностью; иногда необходимо знание предыстории партии: двигался ли король – для возможности рокировки и др.

Описанный граф может содержать контуры, означающие, что ситуации могут повторяться. Для исследования игры удобно использовать развернутую форму ее графа – в виде корневого дерева. Н₀ – корень дерева; ситуации Т (Н₀) соответствует множество вершин 1-го яруса; для каждой вершины a множество Т (a) составляет множество соседних с ней вершин 2-го яруса и т.д. В вершинах четных ярусов (0, 2, 4,...) ход принадлежит первому игроку (А), в нечетных (1, 3, 5,...) – второму (В). При таком представлении игры одна и та же ситуация соответствует многим вершинам, если в нее можно попасть из Н₀ различными путями: в дереве в каждую вершину ведет единст-венный путь из Н₀, определяемый начальным отрезком партии до этой ситуации. Для конечной игры дерево имеет конечное число ярусов, и все концевые вершины (они могут находиться на разных ярусах) соответствуют заключительным ситуациям: им приписаны значения А или В
(или 0 при возможности ничейного исхода). Длину максимального пути назовем длиной игры.

В известной игре «крестики-нолики» на доске 3´3 для 1-го хода начинающего игрока имеется 9 возможностей (если учитывать симметрию, это число сводится до 3: «центр», «угол», «середина стороны», но для простоты не будем этого учитывать). Для ответного хода игрока В – выбор
8 оставшихся полей, для второго хода игрока А – 7 возможностей и т.д. В соответствующем дереве игры корень имеет степень 9, каждая из 9 вершин 1-го яруса связана с корнем и 8 вершинами
2-го яруса; те, в свою очередь, связаны с 7 вершинами 3-го яруса и т.д.

Существенное свойство рассматриваемого нами типа игр: игрок при своем ходе знает, в какой ситуации он находится и в какие ситуации ведет каждый из допустимых ходов. К такому типу игр не относится большинство карточных игр и домино, поскольку игроку обычно не известен расклад; тем самым при выборе хода он не знает текущей ситуации. По другой причине к этому типу игр не относятся, например, нарды или лото, так как возможность выбора хода зависит от результата стохастического эксперимента – бросания игральных костей.

Стратегия f игрока A – это некоторое соответствие 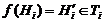, назначающее для каж-дой ситуации H_i, в которой может оказаться игрок А, один определенный ход. Аналогично определяется стратегия игрока В.

Каждая стратегия представляет собой алгоритм игрока, не допускающий вариантов и этим отличающийся от порождающей процедуры – множества допустимых ходов.

Если выбрана стратегия f игрока А и стратегия g игрока В, то тем самым определена пар-тия (f, g), поскольку в каждой не заключительной ситуации однозначно определен переход в следующую ситуацию. Исход игры определяется заключительной ситуацией, в которую приходит партия.

Выбор стратегии игроком А (соответственно, игроком В) означает указание для каждой вершины четного (соответственно, нечетного) яруса дерева игры ровно одной исходящей дуги. Выбор пары стратегий (f, g) выделяет ровно один путь из Н₀ в одну из заключительных вершин.

Примером стратегии начинающего игрока в «крестики-нолики» является, например, следующая: на первом ходу занять центр; далее – занимать клетку, симметричную относительно центра по отношению к клетке, занятой игроком В при предыдущем ходе (можно показать, что она всегда свободна).

В понятии стратегии отсутствует оценка ее качества (удачная – неудачная). Связь с возможным результатом игры устанавливают следующие понятия.

Стратегия f игрока А называется выигрышной, если для любой стратегии g игрока В партия (f, g) заканчивается выигрышем игрока А. Стратегия f игрока А называется беспроигрышной, если для любой стратегии g игрока В партия (f, g) заканчивается выигрышем игрока А или ничьей. Выигрышная и беспроигрышная стратегии игрока В определяются симметрично.

Выигрышная стратегия может быть только у одного из игроков. Беспроигрышная стратегия может быть как у одного, так и у обоих игроков.

Чтобы проиллюстрировать понятие стратегии, рассмотрим игру НИМ. На столе лежат
N спичек. Игрокам разрешается по очереди удалять 1, 2 или 3 спички. Проигрывает тот, кто удаляет последнюю спичку.

Некоторые примеры стратегий начинающего игрока:

– при каждом ходе брать 1 спичку;

– при первом ходе взять 2 спички, а затем брать столько же, сколько взял второй игрок при предыдущем ходе, пока на столе больше 5 спичек; далее – брать 1 спичку.

При N = 20 начинающий игрок обладает выигрышной стратегией: взять при первом ходе
3 спички, и в дальнейшем, при своем ходе брать (4 – b) спичек, где b – число спичек, взятых игроком В на предыдущем ходе. При такой стратегии после хода игрока А на столе будет оставаться последовательно 17, 13, 9, 5, 1 спичек, и игрок В вынужден взять последнюю.

Если же N = 25, то выигрышная стратегия имеется у игрока В: брать всегда (4 – а) спичек, где а – число спичек, взятых игроком А на предыдущем ходе. Тогда после его хода на столе будет оставаться последовательно 21, 17, 13, 9, 5, 1 спичек, и последнюю спичку берет игрок А.

На рис. 2.23 приведено дерево игры НИМ для N = 5. В кружках – число спичек на столе в данной ситуации. Заштрихованные кружки – заключительные позиции с указанием результата (выигрыш А или В).

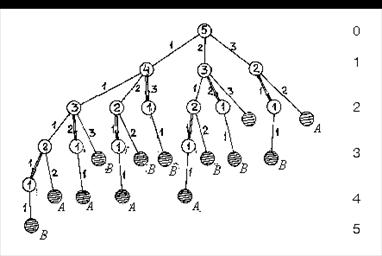
Рис. 2.23

 

Двойными стрелками обозначены наилучшие стратегии игроков (не указан первый ход А и переходы в заключительные позиции, когда нет выбора). Во всех вершинах первого яруса у игрока В есть выигрышные ходы, поэтому при любом первом ходе А игрок В выигрывает, если придерживается указанной стратегии. Для игры НИМ, где результат определяется тем, кто из игроков сделал заключительный ход, все концевые вершины четных ярусов свидетельствуют о выигрыше А, а нечетных ярусов – В. В общем случае игр – это не так.

Для конечной игры справедливы две следующих теоремы.

Теорема 1. Если игра не допускает ничейного исхода, то для одного из игроков существует выигрышная стратегия.

Теорема 2. В игре, допускающей ничейный исход, хотя бы один из игроков обладает беспроигрышной стратегией.

Замечание. Обратите внимание, что в теоремах утверждается не тот очевидный факт, что каждая партия заканчивается в первом случае победой одного из игроков, а во втором – победой или ничьей; смысл первой теоремы – в наличии такой стратегии, следование которой приводит к победе (во втором случае, по крайней мере к ничьей) при любой стратегии противника.

Доказательство теоремы 1 будем вести индукцией по длине игры t.

Если t = 1, то дерево игры имеет вид, изображенный на рис. 2.24, а. Возможны два варианта:

– среди ситуаций Н ₁,..., Н_k (все они – заключительные) имеется ситуация Н_i, помеченная символом А, означающим выигрыш игрока А; в этом случае начинающий имеет выигрышную стратегию f (Н ₀) = Н_i, т.е. выбор хода из Н ₀в Н_i;

– все ситуации Н ₁,..., Н_k помечены символом В; тогда выигрышная стратегия (пустое множество ходов) – у игрока В: начинающий сам при любом своем ходе попадает в заключительную позицию с выигрышем игрока В.

 

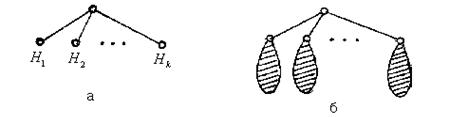
Рис. 2.24

Пусть теперь t > 1 (рис. 2.24 б). Если удалить корень и исходящие из него дуги, то останется некоторое количество корневых поддеревьев, в каждом из которых корнем является вершина
1-го яруса первоначального дерева. Эти поддеревья представляют варианты игры, возникающие после того или иного первого хода игрока А, но начинающим в каждой из ветвей является уже игрок В. Все эти подыгры имеют длину меньше t; поэтому, по предположению индукции, в каждой из них у одной из сторон имеется выигрышная стратегия. Возможны два варианта:

– во всех подыграх выигрышная стратегия у начинающего игрока (В); тогда в исходной игре выигрышная стратегия у игрока В: какой бы первый ход ни выбрал игрок А, его противник В может выбрать свою выигрышную стратегию в полученной подыгре;

– хотя бы в одной из подыгр есть выигрышная стратегия у не начинающего игрока (т.е. А); тогда в исходной игре выигрышная стратегия – у игрока А: она состоит в том, чтобы первым ходом попасть именно в эту подыгру, в ней выбрать свою выигрышную стратегию; в остальных подыграх можно выбрать стратегию произвольно – все равно партия в эти подыгры не переходит. Теорема доказана.

Доказательство теоремы 2 проводится таким же образом. При этом может оказаться, что беспроигрышная стратегия имеется у обоих игроков.

Замечание. Для шахматной (а также шашечной) игры справедлива теорема 2, т.е. либо белые, либо черные, либо обе стороны имеют беспроигрышную стратегию. Однако в настоящее время не известно, у какой именно стороны имеется беспроигрышная стратегия и имеется ли у какой-либо из сторон выигрышная стратегия.

Из доказательства теоремы можно извлечь (по крайней мере теоретический) способ узнать, какая из сторон обладает выигрышной стратегией: начиная с нижних ярусов, определять выигрывающую сторону в подыгре с корнем в предыдущем ярусе и помечать этот корень соответствующим символом А или В до тех пор, пока не будет помечен корень исходной игры: метка корня определяет победителя.

Пример. Дерево игры – на рис. 2.25. Концевые вершины помечены символами А и В. Все вершины 3-го яруса – концевые. Обе внутренние вершины 2-го яруса (7 и 9) соответствуют выбору хода игроком А. Они помечаются символом А, поскольку каждая из них имеет подчиненную вершину 3-го яруса с пометкой А (11 для вершины 7, 14 для вершины 9). Далее, вершины
1-го яруса (2, 3, 4) соответствуют выбору хода игроком В. Вершины 2, 3 помечаются символом В: для вершины 2 имеется подчиненная вершина 6 с пометкой В, для вершины 3 – вершина 8. Вершина 4 вынужденно помечается символом А, так как обе подчиненные ей вершины помечены А. Наконец, корень (вершина 1) – ход игрока А – помечается символом А из-за пометки подчиненной вершины 4. Таким образом, игра – выигрышная для игрока А.

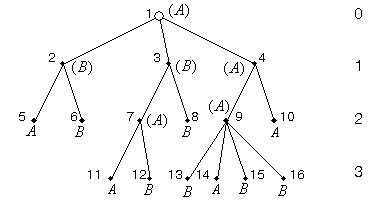
Рис. 2.25

 

 

Правильные раскраски графов

 

Говорят, что вершины (соответственно ребра) неориентирован­ного графа G без петель правильно раскрашены, если каждой вершине (соответственно каждому ребру) графа сопоставлен ровно один из заданного набора цветов, причем любым двум соседним вершинам (соответственно смежным ребрам) сопоставлены разные цвета. Граф, вершины или ребра которого правильно раскрашены, будем называть правильно раскрашенным, если из контекста ясно, какие именно элементы графа раскрашиваются или это безразлично. Очевидно, что всякий подграф правильно раскрашенного графа также правильно раскрашен. Удобно нумеровать цвета натуральными числами 1, 2,.... Отрезок натурального ряда от 1 до k включительно будем обозначать Nk. Можно сказать, что правильная раскраска вершин (соответственно ребер) графа - это функция с натуральными значениями, определенная на множестве вершин (соответственно ребер) и разнозначная на концах каждого ребра (соответственно на ребрах каждой звезды) графа.

Основная задача состоит в определении наименьшего числа χ(G) (соответственно ψ(G)) различных цветов, с помощью которых можно правильно раскрасить вершины (соответственно ребра) графа G. Величина χ(G) называется хроматическим числом, а ψ(G) - хроматическим классом графа G.

При раскраске вершин будем рассматривать графы без петель и кратных ребер, поскольку наличие или отсутствие кратных ребер никак не влияет на правильность раскраски графа. Отметим, что подграф, натянутый на множество вершин, окрашенных одинаково, при правильной раскраске не содержит ребер.

Очевидно, что для всякого графа с b вершинами χ(G) ≤ b, причем равенство достигается только для полного графа: всякий другой граф можно раскрасить меньшим числом цветов, окрасив две несмежные вершины одинаково. С другой стороны, если в графе имеется хотя бы одно ребро, то χ(G) ≥ 2.

Графы, для которых χ(G) = 2, называются бихроматическими. Ясно, что бихроматический граф является двудольным, и наоборот, всякий двудольный граф, содержащий хотя бы одно ребро, бихроматичен. Справедливо и другое условие бихроматичности и тем самым двудольности графа.

Теорема. Для того чтобы граф, содержащий хотя бы одно ребро, был бихроматическим, необходимо и достаточно, чтобы он не содержал элементарных циклов нечетной длины.

Необходимость. Поскольку при правильной раскраске двумя цветами эти цвета на цикле должны чередоваться, вершины цикла нечетной длины не могут быть раскрашены в два цвета, и, следовательно, граф, содержащий этот цикл, не может быть бихроматическим.

Достаточность. Заметим прежде всего, что дерево бихроматично. В самом деле, выберем произвольно корень и используем представление дерева, описанное в п. 2.3. Окрасим все вершины четных ярусов в один цвет, а все вершины нечетных ярусов в другой цвет. Эта раскраска правильная, так как ребра в дереве соединяют только вершины соседних ярусов.

Рассмотрим теперь элементарную цепь, соединяющую в дереве вершину i -го яруса и вершину j -го яруса. На каждом ее ребре происходит изменение номера яруса на единицу. Поэтому ее длина имеет ту же четность, что и число (i – j). В частности, вершины, принадлежащие ярусам одинаковой четности, связаны элементарной цепью четной длины.

Если мы выберем теперь в графе G, не содержащем элементарных циклов нечетной длины, любой остов, то хорды относительно этого остова будут связывать вершины из ярусов разной четности (иначе в графе G появился бы элементарный цикл нечетной длины), т.е. двухцветная правильная раскраска остова будет правильной раскраской и в графе G.

Если граф содержит в качестве подграфа t -вершинный полный граф Kt, то его хроматическое число, очевидно, не меньше t. Противоположное утверждение, однако, неверно. Существуют графы даже без треугольников (полный граф K ₃), имеющие сколь угодно большое хроматическое число. Пример такого графа с хроматическим числом 4 приведен на рис. 2.26.

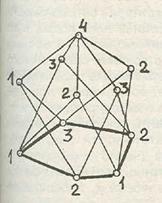
Рис. 2.26

 

Рассмотрим, как связано хроматическое число со степенями вершин графа. Обозначим через s (G) максимальную из степеней вершин графа G, а через Г (s) - класс графов без кратных ребер, для которых s (G) ≤ s. Нетрудно показать индукцией по числу вершин, что если G Î Г (s), то
χ(G) ≤ s + 1. В самом деле, если число вершин в графе меньше или равно (s + 1), то утверждение тривиально. Пусть теперь оно установлено для всех графов из Г (s), имеющих меньше вершин, чем граф G. Удалим из G звезду произвольной вершины a и в соответствии с предположением индукции правильно раскрасим граф G \ Z_a с использованием (s + 1) цветов. В графе G у вершины a не более s соседних вершин, поэтому в множестве цветов N_{s+ 1}есть хотя бы один цвет, которым не окрашена ни одна из вершин, соседних с a. Его можно использовать для окраски вершины a, после чего граф G будет правильно раскрашен (s + 1) цветами.

Полный (s + 1)-вершинный граф K_{s+ 1}представляет собой пример графа из Г(s), для которого хроматическое число равно (s + 1). Оказывается, что этот пример - единственный, а именно спра-ведлива следующая теорема

Теорема. Пусть s ≥ 3. Если G Î Г(s) и G ≠ Ks+1, то χ(G) ≤ s.

 

ПРИЛОЖЕНИЯ

 

Приложение 1

Примеры решения задач

 

Задача 1. Сколько 5-значных чисел, в десятичной записи которых участвуют цифры из множества {0, 1, 4, 6, 7}?

Решение. В записи числа первая цифра должна быть отличной от 0; остальные четыре цифры могут быть произвольными. По комбинаторному правилу произведения искомое число 5-значных чисел равно 4 • 5 • 5 • 5 • 5 = 2500.

Задача 2. Сколько 6-значных чисел, в десятичной записи которых участвуют цифры из множества {0, 1, 4, 6, 7} и таких, что четные цифры чередуются с нечетными?

Решение. Если в записи числа первая цифра четная, то она может быть равна 4 или 6, вторая, четвертая и шестая – 1 или 7, третья и пятая – 0, 4 или 6; таких чисел по правилу произведения:
2 • 2 • 3 • 2 • 3 • 2 = 144. Если же первая цифра нечетная, то она, а также третья и пятая могут быть равны 1 или 7, вторая, четвертая и шестая – 0, 4 или 6; таких чисел 2 • 3 • 2 • 3 • 2 • 3 = 216. Всего искомых чисел 144 + 216 = 360.

Задача 3. Сколько различных слов можно составить перестановками букв слова МАТЕМАТИКА?

Решение. Число перестановок из 10 букв равно 10!. Однако в слове МАТЕМАТИКА
есть одинаковые буквы: М – 2 раза, А – 3 раза, Т – 2 раза: перестановка одинаковых
букв не изменяет слова. Поэтому число различных 10-буквенных слов равно = =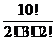
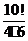= 1 • 2 • 3 • 5 • 7 • 8 • 9 • 10 = [в произведении отсутствуют множители 4 и 6] = 151200.

Задача 4. В формуле W = [(X A Y) B (Y C Z)] D (X E T) F (Z G T) каждый из символов A, B, C, D, E, F, G обозначает одну из арифметических операций: сложение, вычитание, умножение и деление. Сколько различных формул представляются таким образом?

Решение. Каждый из символов A, B, C, D, E, F, G может иметь 4 значения независимо от других. Тем самым, формула однозначно определяется (4, 7)-размещением с повторениями. Поэтому число различных формул равно 4⁷ = 16384.

Задача 5. Сколько существует 7-значных десятичных чисел таких, что в их записи:

а) нет одинаковых цифр в соседних разрядах;

б) в любых трех последовательных разрядах все цифры различны?

Решение. а) Для первой цифры – 9 возможностей (любая цифра, кроме 0); для второй и последующих – любая цифра, кроме предыдущей, также 9 вариантов. Результат – по правилу произведения: 9⁷.

б) Для первой и второй цифры – 9 возможностей, как в первом случае; для третьей и последующих – любая цифра, кроме двух предыдущих (они различны), т.е. 8 вариантов. По правилу произведения получаем: 9² • 8⁵.

Задача 6. Каждое воскресенье каждый из четырех теннисистов команды А проводит с кем-либо из четырех теннисистов команды В по одной игре. Доказать, что в течение полугода найдутся два воскресенья с одним и тем же распределением противников по четырем парам.

Решение. Занумеруем игроков одной из команд. Распределение их противников есть перестановка из 4 элементов. Число n -перестановок P n равно n! Следовательно, составлять различные наборы из 4 пар можно не более, чем 4! = 1 • 2 • 3 • 4 = 24 способами. Полгода составляют 26 недель, поэтому повторение неизбежно.

Задача 7. Чтобы открыть входную дверь в пещеру, Али-Баба должен угадать шифр. Ему известно, что это некоторое число не длиннее 5 цифр, записываемое с использованием только цифр 2, 4, 8. Возможно не более одной попытки в день. Удастся ли Али-Бабе попасть в пещеру в течение года?

Решение. Указанные шифры – это слова в алфавите { 2, 4, 8 }. Число слов длины k в алфавите из трех букв равно 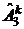= 3 k. Допустимые слова имеют длину от 1 до 5. Число всех таких слов равно сумме 3 + 9 + 27 + 81 + 243 = 363. Поэтому за год можно перебрать все возможные шифры. Не позже 363-го дня дверь откроется.

Задача 8. Книжный коллектор предлагает для комплектования библиотек книги
8 наименований по 1000 экземпляров каждая. Сколькими способами библиотека может составить заявку на 25 книг?

Решение. Заявка указывает, сколько требуется книг каждого наименования. Запасы коллектора позволяют библиотеке выбирать в пределах общего числа 25 книг любое количество книг каждого наименования Соответствующая комбинаторная конфигурация есть (8, 25) -сочетание с повторениями.

Число (n, k)-сочетаний с повторениями: = = 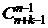. Для заданных параметров получаем: 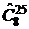= = 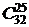= 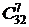(32 • 31 •... • 26) / (1 • 2 •...• 7) = 3365856.

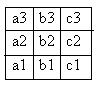
Задача 9. Построить матрицу соседства вершин графа.

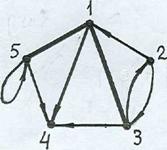
Решение. В графе 5 вершин, поэтому матрица соседства вершин – 5-го порядка. Элемент a_ij матрицы равен 1, если из вершины i идет дуга (ориентированное ребро) в вершину j. Неориентированным ребрам (1, 3) и (1, 5) соответствуют в матрице по две единицы: a ₁₃ = a ₃₁ = 1; a ₁₅ = a ₅₁ = 1. Петле соответствует диагональный элемент a ₅₅.

 

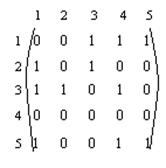
Задача 10. По заданной матрице соседства вершин построить ориентированный граф. Выделить в этом графе какой-нибудь элементарный путь [1, 4] и какую-нибудь элементарную цепь [1, 4].

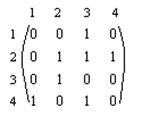
Решение. Порядок матрицы равен 4. Поэтому в графе 4 вершины. Каждая единица в матрице обозначает определенную дугу графа; число дуг равно 7. Обозначим их a, b, c, d, e, f, g.

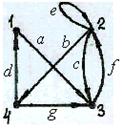
Путь [1, 4] = [1, a, 3, f, 2, b, 4]. Поскольку в графе нет кратных дуг (e и f – кратные ребра, но имеют разные направления), можно опустить обозначения ребер: [1, 3, 2, 4]. В качестве цепи [1, 4] можно рассматривать тот же путь, а также цепи [1, d, 4], [1, a, 3, g, 4].

Задача 11. Найти число треугольников (полных трехвершинников) в полном графе K ₈.

Треугольник полностью определяется выбором трех вершин из данных восьми. Число таких неупорядоченных троек равно числу (8, 3)-сочетаний без повторений

.

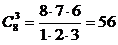Задача 12. Сколько различных циклов длины 4 в полном двудольном графе K _5,8?

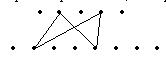
Решение. Множество вершин двудольного графа разбивается на две части А = { a_i } и В = { b_j }. Каждый цикл длины 4 в двудольном графе имеет вид а ₁ b ₁ a ₂ b ₂ a ₁; в полном графе такой
цикл определяется выбором любых двух вершин а ₁и a ₂ из множества А и любых двух вершин
b ₁, b ₂ из множества В (см. чертеж). Неупорядоченную пару вершин { а ₁, a ₂} можно выбрать
С₅² = (5 • 4) / (1 • 2) = 10 способами; неупорядоченную пару вершин { b ₁, b ₂} можно выбрать
С₈² = (8 • 7) / (1 • 2) = 28 способами. По комбинаторному правилу произведения число рассматриваемых циклов равно С₅² • С₈² = 10 • 28 = 280.

Задача 13. Вершинами графа G являются все наборы длины 5 из нулей и единиц. Ребра связывают все пары вершин, различающихся ровно в 2 разрядах. Определить число ребер графа G и его цикломатическое число.

Решение. Число наборов длины k из нулей и единиц равно числу (2, k)-размещений с повторениями: = 2 k. Следовательно число вершин b графа G равно 32. Степень s каждой вершины равна числу наборов, разнящихся с данным в двух разрядах. Число пар таких разрядов равно числу (5, 2)-сочетаний без повторений: 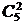= 5 • 4 / 2 = 10. Для однородного графа степени s число ребер равно b · s / 2 = 32 • 5 = 160.

Цикломатическое число связного графа ν(G) = p - b + 1 = 160 – 32 + 1 = 145.

Задача 14. Построить остов графа

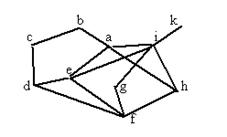
Решение. Выбираем произвольную вершину, например, а, включаем инцидентные ей ребра 1, 2, 3 и, следовательно, вершины b, e, i; далее соседние с ними вершины c, k, h, g и инцидентные им ребра 4, 5, 6, 7, и, наконец, вершины f, d и ребра 8, 9. Выбираемые ребра на каждом этапе подключают к уже построенному к этому моменту подграфу новую вершину, и поэтому циклов не возникает, а связность сохраняется. На чертеже выделенные ребра образуют остов графа. Схема показывает последовательность присоединения вершин в процессе построения остова.

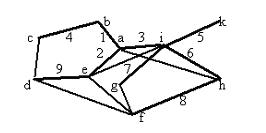
Задача 15. Найти расстояние между вершинами А и В графа с заданными длинами ребер.

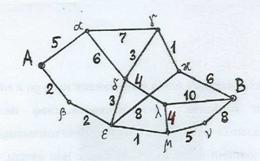
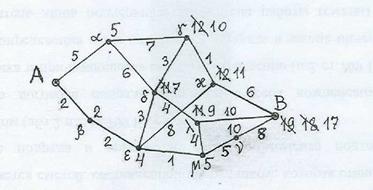
Решение. Длина цепи – сумма длин ее ребер. Расстояние между вершинами – длина кратчайшей цепи, связывающей эти вершины. Алгоритм нахождения искомого расстояния – на чертеже. Показана расстановка меток, выражающих длины цепей, связывающих данную вершину с входным полюсом А. По мере обнаружения более коротких цепей метки пересчитываются (уменьшаются); минимальные вычисленные значения определяют расстояние от А до данной вершины. Последняя метка выходного полюса В есть расстояние d (A, B). Для заданного графа d (A, B) = 17.

Приложение 2

Пример дерева игры

 

В п. 2.7 отмечалось, что в дереве игры «крестики-нолики» на доске 3´3 для 1-го хода начинающего игрока (назовем его +), если учитывать симметрию, число возможностей сводится до 3: «центр» - b₂, «угол» - a₁, «середина стороны» - b₁. Для ответного хода игрока В (его естественно назвать 0) - выбор из 8 оставшихся полей, если учитывать симметрию, зависит от хода, выбранного начинающим и т.д.

 

 

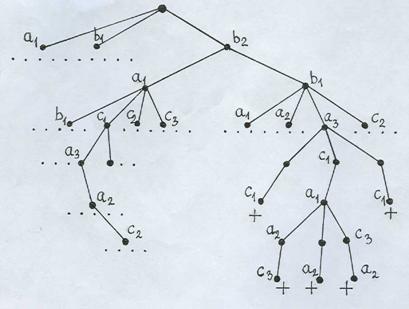
На рис. фрагменты дерева игры: на первом ярусе 3 вершины: a ₁, b ₁, b ₂;
продолжено изображение только ответов на ход b ₂ (с учетом симметрии их 2): «угол» - a ₁, «середина стороны» - b ₁. На ход а ₁ игрока 0 у игрока + есть 4 существенно различных ответа;

на ход с ₁ – указана (не до конца) только форсированная ветвь, которая приводит к ничейному исходу. Если же на 2-м ярусе игроком 0 был выбранход b ₁, у игрока + также есть 4 сущест-венно различных ответа: на рисунке указано только продолжение при выборе хода а ₃: при всех ответах игрока 0 - форсированный выигрыш +.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

 

1. Составьте логическую схему базы знаний по теме юниты:

 

2. Решить задачи 1–8.

Для выполнения работы необходимо определить и записать в таблицу К1 значения переменных а ₁ - а ₄₂(нули и единицы), исходя из следующих параметров:

F – первая буква фамилии,

N – первая буква имени,

S – число букв в фамилии. Впишите свои параметры в табличку:

F =

N =

S =

 

 

(Пример. Евгений Онегин: F = О, N = Е, S = 6.)

Таблица К1

а 1

а 2

а 3

а 4

а 5

а 6

а 7

а 8

а 9

а 10

а 11

а 12

а 13

а 14

а 15

а 16

а 17

а 18

а 19

а 20

а 21

а 22

а 23

а 24

а 25

а 26

а 27

а 28

а 29

а 30

а 31

а 32

а 33

а 34

а 35

а 36

а 37

а 38

а 39

а 40

а 41

а 42

Алгоритм заполнения таблицы К1. Значения а ₁- а ₄₂выбираются из внутреннего кольца круговой диаграммы (рис. 1), разделенной на 28 секторов, которые обозначены буквами от А до Я (во внешнем кольце) и одновременно числами от 1 до 28 (в среднем кольце). Буква Ё считается совпадающей с Е; Й и Ы – совпадающими с И.

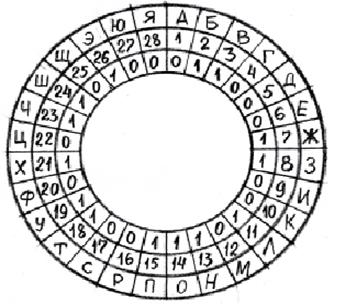
Рис. 1

 

Выбор значений а ₁- а ₄₂производится по следующему правилу:

а ₁- а ₁₄– 14 чисел (нулей и единиц) подряд по часовой стрелке, начиная с позиции F;

а ₁₅- а ₂₈– 14 чисел подряд по часовой стрелке, начиная с позиции N;

а ₂₉- а ₄₂– 14 чисел подряд против часовой стрелки, начиная с позиции S.

Пример заполнения таблицы К1 для F = О, N = Е, S = 6:

а 1

а 2

а 3

а 4

а 5

а 6

а 7

а 8

а 9

а 10

а 11

а 12

а 13

а 14

а 15

а 16

а 17

а 18

а 19

а 20

а 21

а 22

а 23

а 24

а 25

а 26

а 27

а 28

а 29

а 30

а 31

а 32

а 33

а 34

а 35

а 36

а 37

а 38

а 39

а 40

а 41

а 42

 

В каждой из нижеследующих задач (1-8) определенным образом осуществляется выбор переменных 0, 1 из заполненной таблицы К1; из этих цифр составляются многозначные двоичные числа, которые затем используются в качестве параметров (в виде двоичных чисел или переводятся в десятичную систему). Правильное выполнение этих арифметических операций наряду с правильным исполнением инструкции в условии задачи, является неотъемлемой частью решения.

Задача 1. Двузначные двоичные числа b = a ₂₄ a ₂₅, c = a ₂₆ a ₂₇, d = a ₂₈ a ₂₉перевести в десятичную систему. Вычислить m = b + 3, n = b + c + 3, p = d + 5

Заполнить таблицу К2.

Таблица К2

b	c	d	m	n	P

 

Найти число следующих комбинаторных конфигураций:

, , , , , .

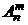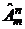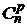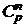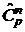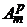Задача 2. Перевести в десятичную систему двузначные двоичные числа t ₁ = а ₁₃ а ₁₄,
t ₂ = а ₁₅ а _{16 ,} t ₃ = а ₁₇ а _18. Определить число различных слов в алфавите { a, b, c }, в которых буква a встречается (t ₁+ 1) раз, буква b встречается(t ₂+ 1) раз, буква c встречается (t ₃+ 1) раз.

Задача 3. Перевести в десятичную систему двузначные двоичные числа а ₁ а ₂, а ₃ а ₄, а ₅ а ₆,

а ₇ а ₈и трехзначные а ₉ а ₁₀ а ₁₁, а ₁₂ а ₁₃ а ₁₄, а ₁₅ а ₁₆ а ₁₇. Сколько различных десятичных чисел (запись которых не начинается с нуля), можно составить из этих семи цифр?

Задача 4. Построить неориентированный граф с пятью вершинами 1, 2, 3, 4, 5, матрицу инциденций и матрицу соседства его вершин. Наличие или отсутствие перечисленных ниже ребер (a, b) определяется значениями однозначных двоичных чисел (1 – ребро присутствует, 0 – ребра нет):

(1, 2) (1, 3) (1, 4) (1, 5) (2, 3) (2, 4) (2, 5) (3, 4) (3, 5) (4, 5);

а ₁₉ а ₂₀ а ₂₁ а ₂₂ а ₂₃ а ₂₄ а ₂₅ а ₂₆ а ₂₇ а ₂₈.

Задача 5. Построить неориентированный граф G с семью вершинами 1, 2, 3, 4, 5, 6, 7 и матрицу соседства его вершин. Считать заданным, что ребра (1, 5), (2, 7), (4, 6) принадлежат графу