Производная функции в точке и на интервале, ее алгебраический, механический и геометрический смысл.
Если существует предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента 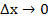 , то он называется значением производной функции f(x) в точке
, то он называется значением производной функции f(x) в точке 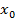
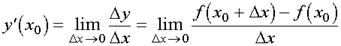
Если в точке x0 существует конечная производная функции y=f(x), то эта функция называется дифференцируемой в точке x0.
Если функция y=f(x) дифференцируема в каждой точке некоторого промежутка, то она дифференцируема на промежутке.
Алгебраический смысл: производная функции в точке есть угловой коэфициент касательной к графику этой функции
Геометрический смысл: угловой коэффициент касательной, приведенной к графику функции y=f(x) в точке x0 равен значению производной функции в этой точке.
Механический смысл: скорость тела равна первой производной координаты по времени:
V(t)=x / (t).
Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение:
a(t)= V / (t)=x // (t).
Правила нахождения производных. Таблица производных. Производная
Сложной функции.
Правила нахождения производных
1. (с*u) ′=с*u′, с=const (постоянный множитель можно выносить за знак производной)
2. Производная суммы двух дифференцируемых функций равна сумме их производных:
(u 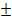 v) ′=u′
v) ′=u′ 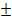 v′
v′
3. Производная произведения двух дифференцируемых функций вычисляется по следующему правилу: (uv) ′=u′v+uv 
4. Производная частного двух дифференцируемых функций вычисляется по следующему правилу:
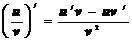
Таблица производных
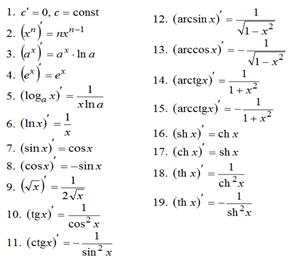
Производная сложной функции
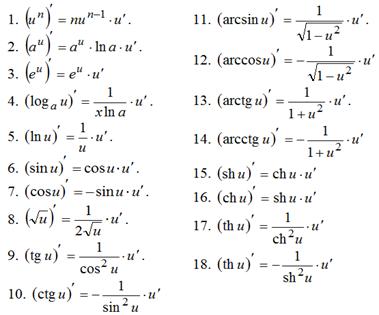
Дифференциал функции, его алгебраический и геометрический смысл.
Свойства дифференциала.
Дифференциал функции равен произведению производной функции на приращение ее аргумента.
Дифференциал функции есть главная часть приращения функции. В этом состоит аналитический смысл дифференциала
Геометрический смысл: дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
Свойства дифференциала: аналогичны свойствам производной.
Производные и дифференциалы второго и высшего порядков.
Дифференциалом второго порядка (или вторым дифференциалом) от функции y=f(x) в точке х 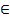 (a; b) называется дифференциал от дифференциала первого порядка функции f(x) в этой точке.
(a; b) называется дифференциал от дифференциала первого порядка функции f(x) в этой точке.
Дифференциалом п-ного порядка от функции f(x) в точке x называется дифференциал от дифференциала (п–1)-го порядка функции f(x) в этой точке:
d 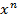 y=d(d
y=d(d 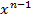 y), где d
y), где d 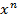 y=f
y=f 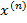 d
d 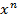 .
.
Производная второго порядка-производная от производной этой функции
Производной n-го порядка функции f(x) наз. производная от производной функции f(x) (n-1)-го порядка 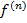 (x)
(x)
Промежутки выпуклости, вогнутости, точки перегиба. Схема исследования
Функции
Кривая называется выпуклой на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая называется вогнутой на интервале (а, b), если все ее точки лежат выше любой ее касательной на этом интервале
Точка, отделяющая выпуклую часть кривой отвогнутой, называется точкой перегиба.
Схема исследования функции
1) Область определения функции.
2) Координаты точек пересечения с осями координат.
3) Четность, нечетность функции.
4) Асимптоты графика и пределы на ±∞. (Если они имеются).
5) Критические точки.
6) Интервалы монотонности и точки экстремума.
7) Промежутки выпуклости и вогнутости, точки перегиба. (Если они имеются).
8) Дополнительные точки, если нет асимптот.
9) Построение графика.
10) Область значения функции.
Неопределенный интеграл, его свойства. Методы вычисления неопределенного интеграла: непосредственное интегрирование. Примеры.
Множество всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x)
Свойства:
1) Производная от неопределенного интеграла равна подынтегральной функции:

2) Дифференциал неопределенного интеграла равен подынтегральному выражению:
D (∫ f(x)dx)=f(x)dx
3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого С:
∫ df(x)=f(x)+C
4) Постоянный множитель можно выносить за знак интеграла
∫ kf(x)dx=k∫f(x)dx
5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx
6) Пусть функция f(x) имеет первообразнуюF(x), тогда
∫f(kx+b)dx= 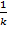 F(kx+b)+C
F(kx+b)+C
Методы вычисления неопределенного интеграла:
1) Метод непосредственного интегрирования (основан на применении свойств интеграла)
∫(1-sinx)dx=∫dx -∫sinxdx=x+cos+C
2) Метод замены переменной(основан на понятии производной сложной функции)

3) Метод интегрирования по частям (по формуле ∫udv=uv-∫udu)
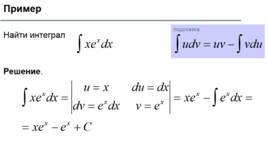
Методы вычисления неопределенного интеграла: интегрирование методом подстановки. Примеры.
Основан на применении свойств интеграла F(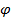 (x))
(x))
Если функция f(t) имеет первооборазнуюF(t), а функция t= 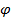 (x) дифференцируема, то функция f(φ(x)) также имеет первообразную:
(x) дифференцируема, то функция f(φ(x)) также имеет первообразную:
∫ f(φ(x))d(φ(x))-F(φ(x)+C

Примеры применения определенного интеграла для решения задач физики,
Химии, биологии
Стр. 73-77
Дифференциальные уравнения в биологии, физике, химии. Примеры.
Cтр.105-109
Производная функции в точке и на интервале, ее алгебраический, механический и геометрический смысл.
Если существует предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента 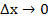 , то он называется значением производной функции f(x) в точке
, то он называется значением производной функции f(x) в точке 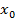
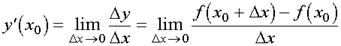
Если в точке x0 существует конечная производная функции y=f(x), то эта функция называется дифференцируемой в точке x0.
Если функция y=f(x) дифференцируема в каждой точке некоторого промежутка, то она дифференцируема на промежутке.
Алгебраический смысл: производная функции в точке есть угловой коэфициент касательной к графику этой функции
Геометрический смысл: угловой коэффициент касательной, приведенной к графику функции y=f(x) в точке x0 равен значению производной функции в этой точке.
Механический смысл: скорость тела равна первой производной координаты по времени:
V(t)=x / (t).
Соответственно, вторая производная функции – скорость изменения скорости, т.е. ускорение:
a(t)= V / (t)=x // (t).
Правила нахождения производных. Таблица производных. Производная
Сложной функции.
Правила нахождения производных
1. (с*u) ′=с*u′, с=const (постоянный множитель можно выносить за знак производной)
2. Производная суммы двух дифференцируемых функций равна сумме их производных:
(u 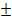 v) ′=u′
v) ′=u′ 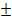 v′
v′
3. Производная произведения двух дифференцируемых функций вычисляется по следующему правилу: (uv) ′=u′v+uv 
4. Производная частного двух дифференцируемых функций вычисляется по следующему правилу:
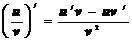
Таблица производных
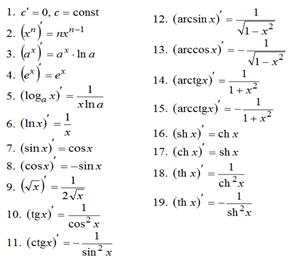
Производная сложной функции
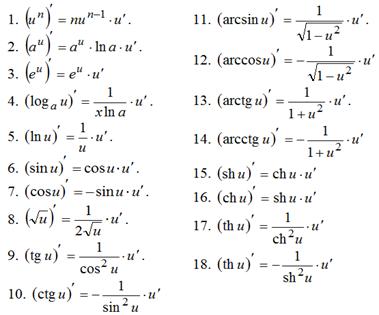



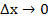 , то он называется значением производной функции f(x) в точке
, то он называется значением производной функции f(x) в точке 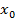
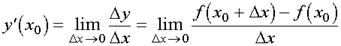
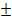 v) ′=u′
v) ′=u′ 
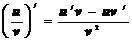
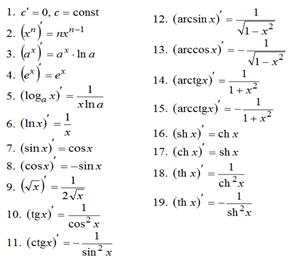
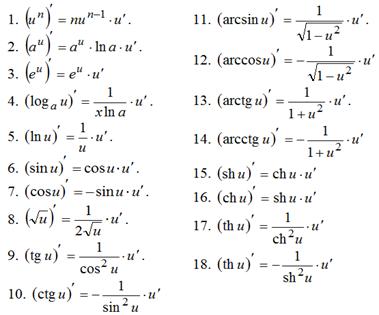
 (a; b) называется дифференциал от дифференциала первого порядка функции f(x) в этой точке.
(a; b) называется дифференциал от дифференциала первого порядка функции f(x) в этой точке. y=d(d
y=d(d 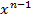 y), где d
y), где d 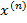 d
d 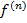 (x)
(x)
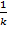 F(kx+b)+C
F(kx+b)+C
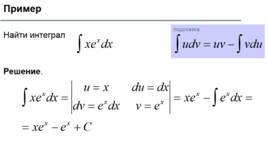
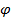 (x))
(x))



