1) (А + В)Т = А Т + В Т;
2) (АВ)Т = В Т А Т;
3) (kА)Т = kА Т;
4) (А –1)Т = (А Т)–1,
где k – число, А и В – матрицы.
Матрица А называется симметрической, если А = А Т.
Ортогональной называется матрица А, для которой А Т = А –1.
Следующие три условия равносильны:
1) матрица А ортогональна;
2) матрица А –1 ортогональна;
3) столбцы матрицы А образуют ортонормированную систему векторов.
Ортогональная матрица может не иметь действительных собственных значений.
Симметрическая матрица всегда имеет действительные собственные значения, и все ее собственные значения – действительные числа. Собственные векторы симметрической матрицы, принадлежащие различным собственным значениям, ортогональны.
Для каждой симметрической матрицы А существует такая ортогональная матрица Q, что
Q –1 А Q – диагональная матрица. Построение этой ортогональной матрицы осуществляется следующим образом:
1) строим невырожденную матрицу Т, которая приводит матрицу А к диагональному виду;
2) подвергаем столбцы найденной матрицы Т процессу ортогонализации Шмидта, а затем нормируем полученные векторы;
3) строим ортогональную матрицу Q, столбцами которой являются координаты полученной в п.2 ортонормированной системы векторов.
Пример. Привести к диагональному виду с помощью ортогональной матрицы симметрическую матрицу А = 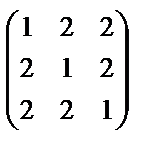 .
.
Р е ш е н и е. Характеристическое уравнение матрицы А имеет вид:
| A – λE |= 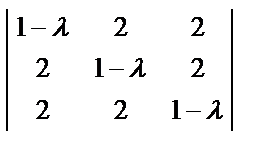
 =
= 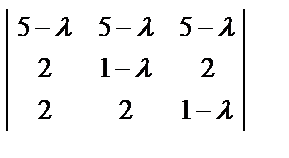 = (5 – λ)
= (5 – λ) 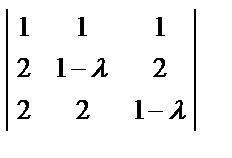
 = (5 – λ)
= (5 – λ) 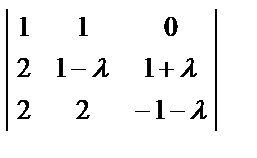 = (5 – λ) (1 + λ)
= (5 – λ) (1 + λ) 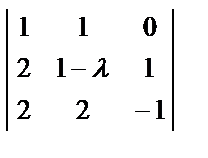
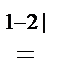 (5 – λ) (1 + λ)
(5 – λ) (1 + λ) 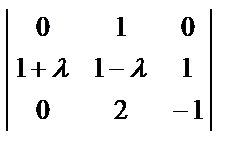 =(5 – λ) (1 + λ)2 = 0.
=(5 – λ) (1 + λ)2 = 0.
Отсюда следует, что матрица А имеет два собственных значения: λ 1 = –1, λ 2 = 5.
Фундаментальная система решений системы уравнений (A + E) х = θ состоит из двух векторов
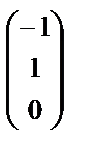 и
и 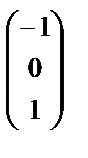 , а система уравнений(A – 5 E) х = θ – из одного вектора
, а система уравнений(A – 5 E) х = θ – из одного вектора 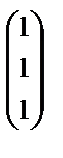 (вычисления провести самостоятельно).
(вычисления провести самостоятельно).
Матрица Т, приводящая матрицу А к диагональному виду, имеет вид Т =  .
.
После ортогонализации и нормирования столбцов этой матрицы получим ортогональную матрицу
Q =  .
.
Матрица, обратная к Q, совпадает с Q Т, т.е., Q –1 = 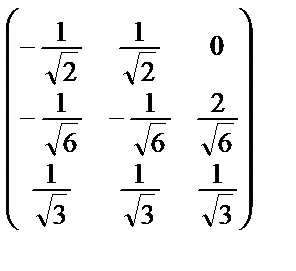 .
.
Нетрудно проверить, что Q –1 А Q = 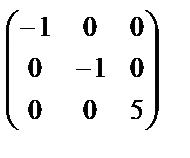 .
.
Задания. Привести к диагональному виду с помощью ортогональной матрицы следующие матрицы:
1. А = 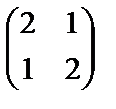 , 2. А 2 =
, 2. А 2 = 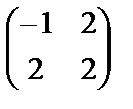 , 3. А 3 =
, 3. А 3 = 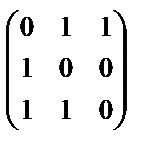 , 4. А 4 =
, 4. А 4 = 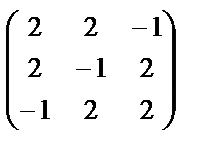 .
.
2.4. Квадратичные формы
Переход от системы n неизвестных х 1, х 2, …, хn к системе n неизвестных
у 1, у 2, …, уn по формуле x = S y, где х = х (х 1, х 2, …, хn), у = у (у 1, у 2, …, уn), S – квадратная матрица порядка n, называется линейным преобразованием неизвестных. Если S – невырожденная матрица, то линейное преобразование неизвестных также называется невырожденным.
Квадратичной формой F (х 1, х 2, …, хn) от n неизвестных х 1, х 2, …, хn называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных
F (х) = 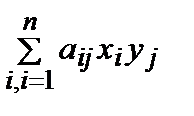 . (1)
. (1)
Квадратичную форму можно записать в виде F (х) = х А х, где х = (х 1, х 2, …, хn),
А – симметрическая матрица порядка n, которая называется матрицей квадратичной формы F (х).
Две квадратичные формы называются эквивалентными, если одна из них переводится в другую посредством невырожденного линейного преобразования.
Если в квадратичной форме F (х) = х А х неизвестные подвергнуть линейному преобразованию x = S y, то получится квадратичная форма F (у) = у (S T А S) y с матрицей S T А S.
Каноническим видом данной квадратичной формы называется эквивалентная ей форма, не содержащая произведений неизвестных. Каждую квадратичную форму можно привести к каноническому виду с помощью линейного преобразования неизвестных
x = S y с ортогональной матрицей S. Столбцами матрицы S являются координаты некоторого ортонормированного базиса B н =(e 1,..., e n), в котором матрица A имеет диагональный вид D = S T А S. D − диагональная матрица, на диагонали которой стоят собственные числа матрицы.
Если F (х) > 0 (< 0) для всех х ≠ θ, то квадратичная форма F (х) называется положительно (отрицательно) определенной. Квадратичная форма положительно (отрицательно) определена, если в каком-нибудь ее каноническом виде нет отрицательных (положительных) коэффициентов при квадратах неизвестных.
Критерием положительной определенности квадратичной формы является следующее утверждение (критерий Сильвестра): для того, чтобы квадратичная форма А (х, х) была положительно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы А были положительны, т.е. Dk > 0, k = 1, 2, …, n.
Следующие условия равносильны:
1) квадратичная форма F (х) = х А х положительно определена;
2) собственные значения матрицы А положительны;
3) угловые миноры матрицы А положительны.
Следующие условия равносильны:
1) квадратичная форма F (х) = х А х отрицательно определена;
2) собственные значения матрицы А отрицательны;
3) все угловые миноры матрицы А нечетного порядка отрицательны, а все угловые миноры четного порядка положительны.
Пример 1. Написать матрицу квадратичной формы
F = 2  – 5
– 5  + 8
+ 8  + 4 x 1 x 2 – 2 x 1 x 3 + 6 x 2 x 3.
+ 4 x 1 x 2 – 2 x 1 x 3 + 6 x 2 x 3.
Р е ш е н и е. Обозначим коэффициент при произведении x i x k = x k x i (i ≠ k) через
аik + аki, причем аik = аki. Член (аik + аki) x i x k запишем в виде аikxixk + аkixkxi. Тогда квадратичную форму F можно записать в виде
F = 2 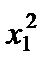 + 2 x 1 x 2 – x 1 x 3 + 2 x 2 x 1 – 5
+ 2 x 1 x 2 – x 1 x 3 + 2 x 2 x 1 – 5 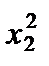 + 3 x 2 x 3 – x 3 x 1 + 3 x 3 x 2 + 8
+ 3 x 2 x 3 – x 3 x 1 + 3 x 3 x 2 + 8 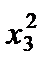 .
.
Теперь матрица А квадратичной формы имеет вид: A = 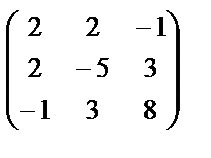 .
.



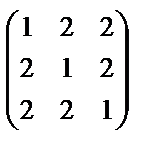 .
.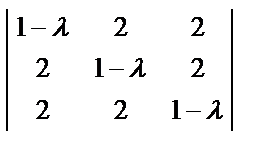
 =
= 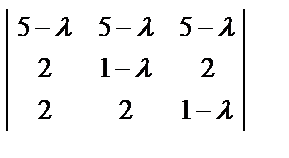 = (5 – λ)
= (5 – λ) 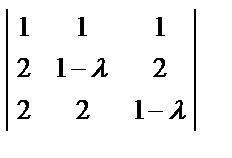
 = (5 – λ)
= (5 – λ) 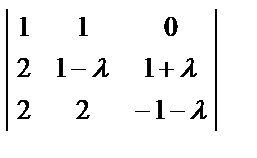 = (5 – λ) (1 + λ)
= (5 – λ) (1 + λ) 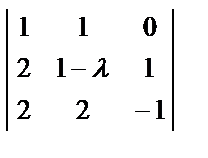
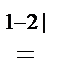 (5 – λ) (1 + λ)
(5 – λ) (1 + λ) 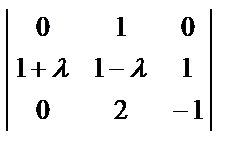 =(5 – λ) (1 + λ)2 = 0.
=(5 – λ) (1 + λ)2 = 0.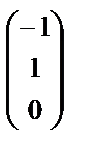 и
и 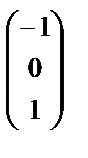 , а система уравнений(A – 5 E) х = θ – из одного вектора
, а система уравнений(A – 5 E) х = θ – из одного вектора  (вычисления провести самостоятельно).
(вычисления провести самостоятельно). .
. .
. .
.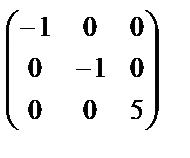 .
.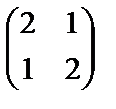 , 2. А 2 =
, 2. А 2 = 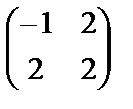 , 3. А 3 =
, 3. А 3 = 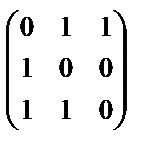 , 4. А 4 =
, 4. А 4 = 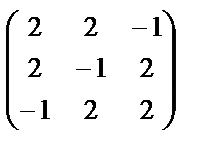 .
.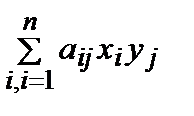 . (1)
. (1) – 5
– 5  + 8
+ 8  + 4 x 1 x 2 – 2 x 1 x 3 + 6 x 2 x 3.
+ 4 x 1 x 2 – 2 x 1 x 3 + 6 x 2 x 3.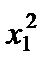 + 2 x 1 x 2 – x 1 x 3 + 2 x 2 x 1 – 5
+ 2 x 1 x 2 – x 1 x 3 + 2 x 2 x 1 – 5 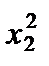 + 3 x 2 x 3 – x 3 x 1 + 3 x 3 x 2 + 8
+ 3 x 2 x 3 – x 3 x 1 + 3 x 3 x 2 + 8 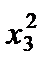 .
.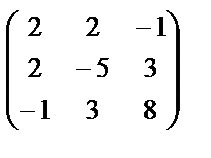 .
.


