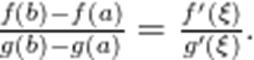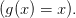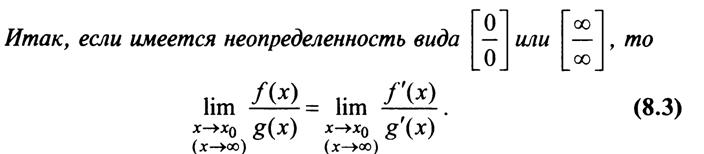Производная функции в точке, ее геометрический смысл.
Определение. Производной функции у = f{x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю {если этот предел существует):
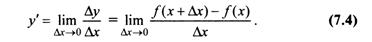
Н𝜟хождение производной функции называется дифференцированием этой функции.
Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. геометрический смысл производной: производная 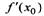 есть угловой коэффициент {тангенс угла наклона) касательной, проведенной к кривой y=f{x) в точке
есть угловой коэффициент {тангенс угла наклона) касательной, проведенной к кривой y=f{x) в точке 
Тогда уравнение касательной к кривой 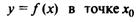 примет вид
примет вид 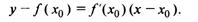
Производная алгебраической суммы функций, произведения и частного.
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих
функций, т.е. 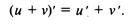
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. 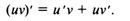
Производная частного двух дифференцируемых функций может быть найдена по формуле 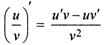
Общая схема нахождения производных функций.
Производная функции у =f(x) может быть найдена по следующей схеме:
1. Дадим аргументу х приращение 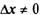 и найдем наращенное значение функции
и найдем наращенное значение функции 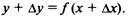
2. Находим приращение функции 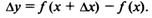
3. Составляем отношение 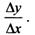
4. Находим предел этого отношения при 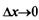 , т.е.
, т.е. 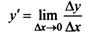
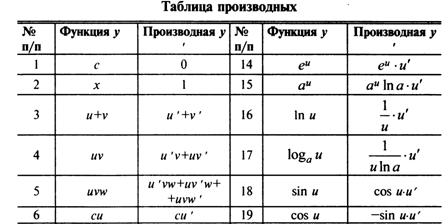
(это не к вопросу, но знать нужно)


Правило дифференцирования сложной функции.
Пусть переменная у есть функция от переменной 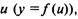 а переменная u в свою очередь есть функция от независимой переменной х:, т.е. задана сложная функция
а переменная u в свою очередь есть функция от независимой переменной х:, т.е. задана сложная функция 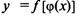
Теорема. Если 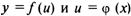 — дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного
— дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного
аргумента по независимой переменной х, т.е. 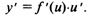
Правило дифференцирования сложной функции может
быть записано и в других формах: 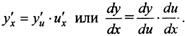
Дифференцирование неявных функций.
Рассмотрим дифференцирование неявной функции, заданной урав-
нением F{x, у) = 0
Для нахождения производной функции у, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая у как функцию от х, а затем из полученного уравнения найти производную у'.
Найти производную функции у, заданной уравнением 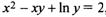 , и вычислить ее значение в точке (2; 1).
, и вычислить ее значение в точке (2; 1).
Решение. Дифференцируя обе части равенства и учитывая,
что у есть функция от х, получим 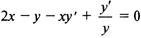 , откуда
, откуда
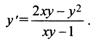
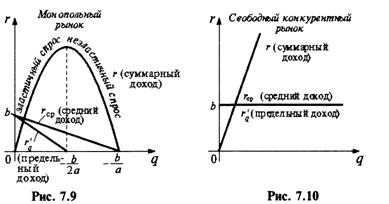
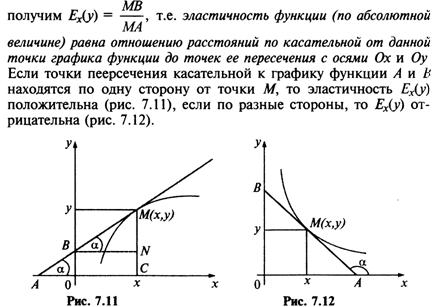
Экономический смысл производной. Использование понятия производной в экономике.










 \
\ 

Теорема Ферма.
Теорема Ферма. Если дифференцируемая на промежутке X функция у =f(x) достигает наибольшего или наименьшего значения во внутренней точке 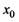 этого промежутка, то производная функции в этой точке равна нулю, т.е.
этого промежутка, то производная функции в этой точке равна нулю, т.е. 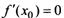
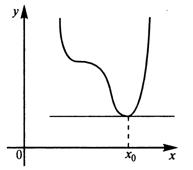
Геометрический смысл теоремы Ферма очевиден: в точке наибольшего или наименьшего значения, достигаемого внутри промежутка X, касательная к графику функции параллельна оси абсцисс.
Теорема Ролля.
Пусть функция у =f(x) удовлетворяет следующим условиям:
1) непрерывна на отрезке [а, Ь];
2) дифференцируема на интервале (а, Ь);
3) на концах отрезка принимает равные значения, т.е.
f(a)=f{b).
Тогда внутри отрезка существует по крайней мере одна такая
точка 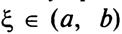 , в которой производная функции равна нулю:
, в которой производная функции равна нулю:
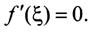
Отметим геометрический
смысл теоремы Ролля: найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс, в этой точке производная и будет равна нулю (заметим, что на рис. 8.2 таких точек две: Если f{a) =f(b) = О, то теорему
Ролля можно сформулировать так: между двумя последователь-
ными нулями дифференцируемой функции имеется хотя бы один
нуль производной.
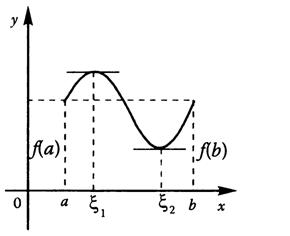
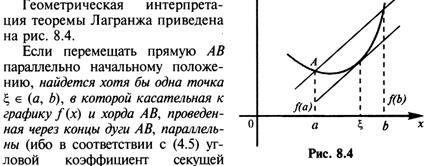
Теорема Лагранжа.
Теорема Ролля является частным случаем теоремы Лафанжа.
Теорема Лагранжа. Пусть функция у =f(x) удовлетворяет следующим условиям:
1) непрерывна на отрезке [а, Ь]\
2) дифференцируема на интервале {а, Ь).
Тогда внутри отрезка существует по крайней мере одна такая
точка 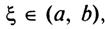 в которой производная равна частному от деления
в которой производная равна частному от деления
приращения функции на приращение аргумента на этом отрезке, т.е.
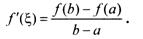
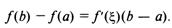


Теорема Коши.
Если функции 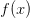 и
и 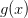 непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем
непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем 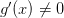 во всех точках этого интервала, то найдется хотя бы одна точка
во всех точках этого интервала, то найдется хотя бы одна точка 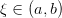 такая, что
такая, что
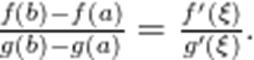
1. Замечание. Теорема Лагранжа — частный случай теоремы Коши 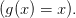
2. Замечание. Теорему Коши нельзя получить используя теорему Лагранжа отдельно к числителю и к знаменателю.
Правило Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных {конечному или бесконечному), если последний существует в указанном смысле.
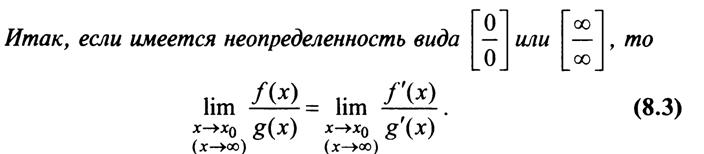
Производная функции в точке, ее геометрический смысл.
Определение. Производной функции у = f{x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю {если этот предел существует):
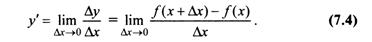
Н𝜟хождение производной функции называется дифференцированием этой функции.
Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. геометрический смысл производной: производная 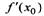 есть угловой коэффициент {тангенс угла наклона) касательной, проведенной к кривой y=f{x) в точке
есть угловой коэффициент {тангенс угла наклона) касательной, проведенной к кривой y=f{x) в точке 
Тогда уравнение касательной к кривой 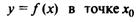 примет вид
примет вид 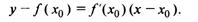



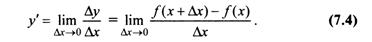
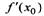 есть угловой коэффициент {тангенс угла наклона) касательной, проведенной к кривой y=f{x) в точке
есть угловой коэффициент {тангенс угла наклона) касательной, проведенной к кривой y=f{x) в точке 
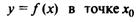 примет вид
примет вид 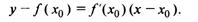
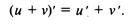
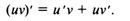
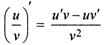
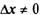 и найдем наращенное значение функции
и найдем наращенное значение функции 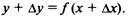
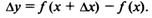
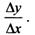
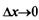 , т.е.
, т.е. 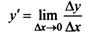



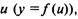 а переменная u в свою очередь есть функция от независимой переменной х:, т.е. задана сложная функция
а переменная u в свою очередь есть функция от независимой переменной х:, т.е. задана сложная функция 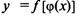
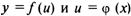 — дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного
— дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и, умноженной на производную самого промежуточного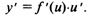
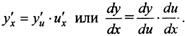
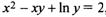 , и вычислить ее значение в точке (2; 1).
, и вычислить ее значение в точке (2; 1).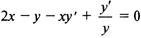 , откуда
, откуда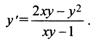












 \
\ 

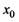 этого промежутка, то производная функции в этой точке равна нулю, т.е.
этого промежутка, то производная функции в этой точке равна нулю, т.е. 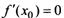

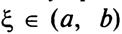 , в которой производная функции равна нулю:
, в которой производная функции равна нулю: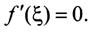

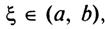 в которой производная равна частному от деления
в которой производная равна частному от деления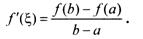
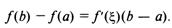



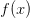 и
и 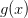 непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем
непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем 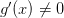 во всех точках этого интервала, то найдется хотя бы одна точка
во всех точках этого интервала, то найдется хотя бы одна точка 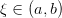 такая, что
такая, что