

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
381. Точки разрыва функции и их классификация.
Точка а называется точкой разрыва функции  , если функция
, если функция  не является непрерывной в этой точке.
не является непрерывной в этой точке.
Если 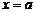 – точка разрыва функции
– точка разрыва функции 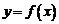 , то в ней не выполняется, по крайней мере, одно из условий первого определения непрерывности функции, а именно:
, то в ней не выполняется, по крайней мере, одно из условий первого определения непрерывности функции, а именно:
1. Функция определена в некоторой окрестности точки а, но не определена в самой точке а.
Например, функция  не определена в точке
не определена в точке 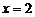 (рис. 1).
(рис. 1).
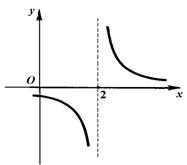 Рис. 1
Рис. 1
| 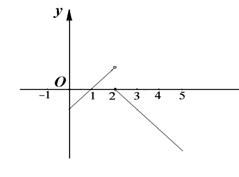 Рис. 2
Рис. 2
|
2. Функция определена в точке а и ее окрестности, но не существует предела 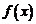 при
при 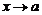 .
.
Например, функция
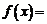
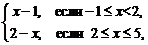 (1)
(1)
определена в точке 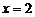
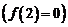 , однако в точке
, однако в точке 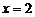 имеет разрыв (рис. 2), т. к. эта функция не имеет предела в этой точке:
имеет разрыв (рис. 2), т. к. эта функция не имеет предела в этой точке:
 , а
, а 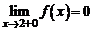 .
.
3. Функция определена в точке а и ее окрестности и существует 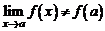 .
.
Например, рассмотрим функцию (рис. 3)
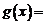
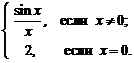 (2)
(2)
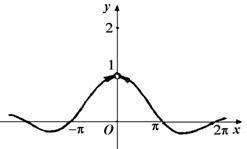
Рис. 3
Здесь 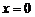 – точка разрыва функции
– точка разрыва функции 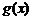 , т.к.
, т.к. 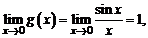 а
а 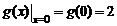 .
.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Точка а называется точкой разрыва первого рода функции 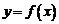 , если в этой точке существуют конечные пределы функции слева и справа, т.е.
, если в этой точке существуют конечные пределы функции слева и справа, т.е. 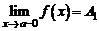 и
и 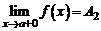 . При этом:
. При этом:
а) если 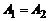 , то точка а называется точкой устранимого разрыва; б) если
, то точка а называется точкой устранимого разрыва; б) если 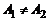 , то точка а называется точкой конечного разрыва. Величину
, то точка а называется точкой конечного разрыва. Величину 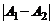 называют скачком функции в точке разрыва
называют скачком функции в точке разрыва 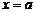 .
.
Точка а называется точкой разрыва второго рода функции 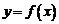 , если по крайней мере один из односторонних пределов (слева или справа) не существует.
, если по крайней мере один из односторонних пределов (слева или справа) не существует.
Так, функция  (рис. 1) имеет разрыв второго рода в точке
(рис. 1) имеет разрыв второго рода в точке 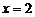 . Для функции (1) (рис. 2) точка
. Для функции (1) (рис. 2) точка 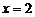 является точкой разрыва первого рода со скачком, равным
является точкой разрыва первого рода со скачком, равным 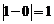 . Точка
. Точка 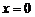 является точкой разрыва первого рода для функции (2) (рис. 3). Положив
является точкой разрыва первого рода для функции (2) (рис. 3). Положив 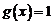 (вместо
(вместо 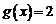 ) при
) при 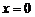 , разрыв устранится, функция станет непрерывной в точке
, разрыв устранится, функция станет непрерывной в точке 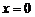 .
.
382. Непрерывность элементарных функций.
|
|
Разумеется, имеется бесконечно много разных функций. Однако среди них выделяется класс элементарных функций. К ним относятся:
а) степенная функция у=xn;
Функция y=xm, где m – произвольное вещественное число, называется степенной функцией. В общем случае считается, что она определена для x>0, хотя при некоторых частных значениях m (например, когда m - целое число) она имеет смысл и при x<0.
Графики этой функции имеют различный вид при разных m.
а) 0<m<1.В этом случае y=xm определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.
б) m>1.В этом случае y=xm определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.
б) m<0.В этом случае y=xm определена для всех x>0 и 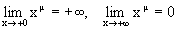 . Она является строго монотонно убывающей функцией и непрерывна для всех x>0.
. Она является строго монотонно убывающей функцией и непрерывна для всех x>0.
б) показательная функция у=ax;
Функция y=ax называется показательной функцией. Число a является произвольным положительным вещественным числом, т.е. a>0. Функция определена и непрерывна для всех вещественных х. Ее графики имеют различный вид в зависимости от значения а.
При a>1 y=ax строго монотонно возрастает. 
При 0<a<1 y=ax строго монотонно убывает. 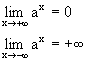
Основным свойством показательной функции является следующее свойство:
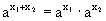
Можно показать, что среди непрерывных функций показательная функция – единственная функция, удовлетворяющая свойству f(x1+x2)=f(x1)f(x2).
Следствием этого свойства является следующее: (ax)m=axm
в) логарифмическая функция у=loga(x);
Функция, обратная ax, называется логарифмической функцией, и обозначается logax. Ее свойства получаются как следствия свойств функции ax.
а) а>0
Так как ax строго непрерывна, то и logax тоже непрерывна.
б)0<x<1
log ax непрерывна.
Можно показать, что logax – единственная непрерывная функция, удовлетворяющая свойству.
г) гиперболические функции sh(x), ch(x), th(x);
С функцией ex тесно связаны функции, получившие название гиперболических. К ним относятся:
|
|
гиперболический синус 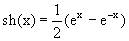
гиперболический косинус 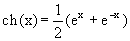
гиперболический тангенс 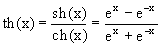
Рассмотрим коротко свойства этих функций.
th(-x)= –th(x)
ch(-x)= ch(x)
т.е. sh(x) и th(x) являются нечетными функциями, а ch(x) – четной функцией. Графики их изображены на рисунках.
д) тригонометрические функции sin(x), cos(x), tg(x);
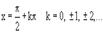 Т.к. эти функции подробно изучаются в школе, то напоминать их свойства мы не будем. Укажем лишь, что sinus(x) и cos(x) непрерывны для всех x, а имеет разрывы второго рода в точках, где cos(x)=0, т.е. в точках
Т.к. эти функции подробно изучаются в школе, то напоминать их свойства мы не будем. Укажем лишь, что sinus(x) и cos(x) непрерывны для всех x, а имеет разрывы второго рода в точках, где cos(x)=0, т.е. в точках
|
|
|

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!