Использование метода наименьших квадратов на фондовой бирже.
Метод наименьших квадратов.
Рассмотрим систему линейных уравнений (1) 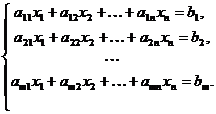 Предположим, что система (1) является результатом исследования, а вектор
Предположим, что система (1) является результатом исследования, а вектор 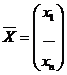 – результатом практических наблюдений. В каком случае можно утверждать, что фактические данные подтверждают теорию?
– результатом практических наблюдений. В каком случае можно утверждать, что фактические данные подтверждают теорию?
Случаи, когда 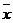 удовлетворяет системе (1), то есть подтверждает теорию, встречаются редко. Будем считать, что
удовлетворяет системе (1), то есть подтверждает теорию, встречаются редко. Будем считать, что 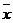 не опровергает теорию, если является хотя бы примерным решением системы (1). В таком случае разность
не опровергает теорию, если является хотя бы примерным решением системы (1). В таком случае разность 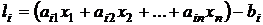 – является
– является 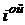 ошибкой системы. Ошибку S(x) всей системы (1) можно определить по крайней мере одним из трех способов:
ошибкой системы. Ошибку S(x) всей системы (1) можно определить по крайней мере одним из трех способов:
1. 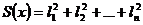
2. 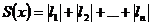
3. 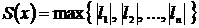 .
.
Алгоритм поиска наименьшего значения функции 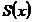 , то есть наименьшей ошибки, является наиболее простым в первом случае, что объясняет популярность метода наименьших квадратов. Метод наименьших квадратов широко используется при анализе статических данных для выявления функциональной зависимости между наблюдаемыми величинами, причем количество наблюдаемых величин не имеет принципиального значения.
, то есть наименьшей ошибки, является наиболее простым в первом случае, что объясняет популярность метода наименьших квадратов. Метод наименьших квадратов широко используется при анализе статических данных для выявления функциональной зависимости между наблюдаемыми величинами, причем количество наблюдаемых величин не имеет принципиального значения.
Применение метода наименьших квадратов (случай линейной зависимости).
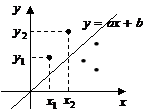 На практике часто возникает задача о наилучшем подборе эмпирических функций, позволяющих представить в аналитической форме данные статических наблюдений.
На практике часто возникает задача о наилучшем подборе эмпирических функций, позволяющих представить в аналитической форме данные статических наблюдений.
Рассмотрим случай, когда наблюдаются две величины x и y, между которыми предполагается наличие функциональной зависимости 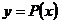 . Пусть многочлен
. Пусть многочлен 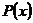 имеет степень 1, то есть предполагается линейная зависимость между величинами x и y вида
имеет степень 1, то есть предполагается линейная зависимость между величинами x и y вида 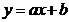 . Параметры a и b необходимо подобрать таким образом, чтобы прямая была расположена как можно ближе к точкам
. Параметры a и b необходимо подобрать таким образом, чтобы прямая была расположена как можно ближе к точкам 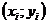 . Пусть
. Пусть 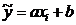 – предполагаемое значение.
– предполагаемое значение.
Если 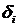 – отклонение экспериментальных точек от предполагаемой прямой, то
– отклонение экспериментальных точек от предполагаемой прямой, то 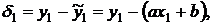
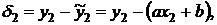 …
… 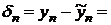
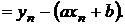
Составим сумму квадратов отклонений 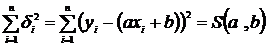 .
.
Потребуем, чтобы эта сумма была наименьшей согласно необходимому условию существования экстремума функции двух переменных. Имеем 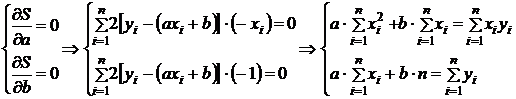 .
.
С помощью последней системы, и, имея экспериментальные значения 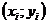 , можно вычислить a и b, что позволит устанавливать приближенную линейную зависимость
, можно вычислить a и b, что позволит устанавливать приближенную линейную зависимость 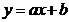 . Для этого разделим обе части обоих уравнений на число наблюдений п. Получим
. Для этого разделим обе части обоих уравнений на число наблюдений п. Получим
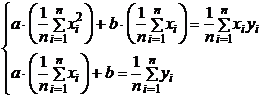 . Введём обозначения
. Введём обозначения 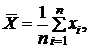
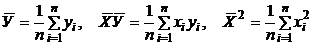 , тогда система примет вид
, тогда система примет вид 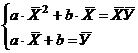 , где
, где 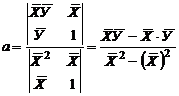 ,
,
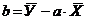 по формулам Крамера.
по формулам Крамера.
Пример 1. Пусть имеем данные о размерах покупок y и их розничной цене x
для некоторого товара. Составить уравнение спроса, пользуясь МНК.
Для удобства использования системы (1) составим таблицу:
Тогда 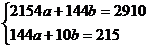
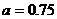 ,
, 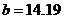
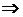
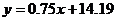 - уравнение спроса.
- уравнение спроса.



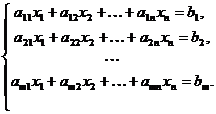 Предположим, что система (1) является результатом исследования, а вектор
Предположим, что система (1) является результатом исследования, а вектор 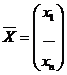 – результатом практических наблюдений. В каком случае можно утверждать, что фактические данные подтверждают теорию?
– результатом практических наблюдений. В каком случае можно утверждать, что фактические данные подтверждают теорию?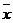 удовлетворяет системе (1), то есть подтверждает теорию, встречаются редко. Будем считать, что
удовлетворяет системе (1), то есть подтверждает теорию, встречаются редко. Будем считать, что 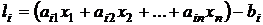 – является
– является 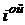 ошибкой системы. Ошибку S(x) всей системы (1) можно определить по крайней мере одним из трех способов:
ошибкой системы. Ошибку S(x) всей системы (1) можно определить по крайней мере одним из трех способов: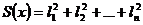
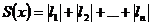
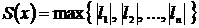 .
.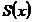 , то есть наименьшей ошибки, является наиболее простым в первом случае, что объясняет популярность метода наименьших квадратов. Метод наименьших квадратов широко используется при анализе статических данных для выявления функциональной зависимости между наблюдаемыми величинами, причем количество наблюдаемых величин не имеет принципиального значения.
, то есть наименьшей ошибки, является наиболее простым в первом случае, что объясняет популярность метода наименьших квадратов. Метод наименьших квадратов широко используется при анализе статических данных для выявления функциональной зависимости между наблюдаемыми величинами, причем количество наблюдаемых величин не имеет принципиального значения.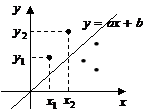 На практике часто возникает задача о наилучшем подборе эмпирических функций, позволяющих представить в аналитической форме данные статических наблюдений.
На практике часто возникает задача о наилучшем подборе эмпирических функций, позволяющих представить в аналитической форме данные статических наблюдений.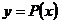 . Пусть многочлен
. Пусть многочлен 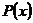 имеет степень 1, то есть предполагается линейная зависимость между величинами x и y вида
имеет степень 1, то есть предполагается линейная зависимость между величинами x и y вида 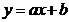 . Параметры a и b необходимо подобрать таким образом, чтобы прямая была расположена как можно ближе к точкам
. Параметры a и b необходимо подобрать таким образом, чтобы прямая была расположена как можно ближе к точкам 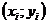 . Пусть
. Пусть 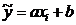 – предполагаемое значение.
– предполагаемое значение.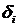 – отклонение экспериментальных точек от предполагаемой прямой, то
– отклонение экспериментальных точек от предполагаемой прямой, то 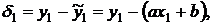
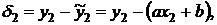 …
… 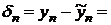
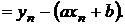
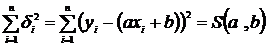 .
.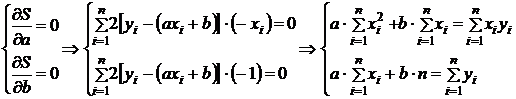 .
.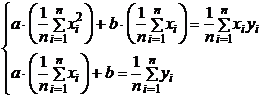 . Введём обозначения
. Введём обозначения 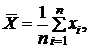
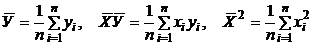 , тогда система примет вид
, тогда система примет вид 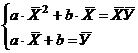 , где
, где 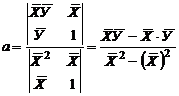 ,
,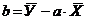 по формулам Крамера.
по формулам Крамера.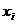
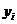
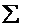
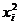
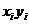
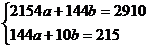
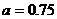 ,
, 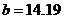
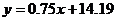 - уравнение спроса.
- уравнение спроса.


