Решение алгебраических уравнений

Функция Solve[eqns, vars] ищет решение системы уравнений eqns относительно переменных vars. В частном случае система может состоять из одного уравнения. Solve[eqns] ищет решение для всех переменных в системе eqns. Уравнения задаются в виде: lhs==rhs – левая и правая части уравнения связаны логическим знаком равенства. Система может быть представлена в виде списка уравнений, либо уравнения могут быть объединены знаком конъюнкции (&&). Решение записывается в форме правил замены: x–>so Решение может быть найдено как в численном, так и в аналитическом виде.

Пример 13.8: Решение системы линейных уравнений:

In[ ]: = Solve[ x + 2y == 0 && 2x – y == 5a, {x, y}]

Out[ ] = {{x –> 2 a, y –> -a}}

При наличии нескольких решений функция Solve дает их список.

Пример 13.9: In[ ]: = Solve[x (y + b) == a^2&&x – y == b, {x, y}]

Out[ ] = {y –> -a - b, x –> -a}, {y –> a - b, x –> a}}

Если имеется корень кратности m, Solve выписывает решение m раз, например:

Пример 13.10: In[ ]: = Solve[ (x – 1)^2 == 0]

Out[ ] = {{ x –> 1}, { x –> 1}}

Функция Solve применима, когда точное решение может быть записано в явном виде.

Функция LinearSolve[m, b] предназначена для решения систем линейных алгебраических уравнений. Эта функция находит решение системы: 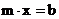, где m – матрица, b и x – известный и неизвестный векторы. Функция LinearSolve позволяет также находить решение сразу нескольких систем уравнений с одинаковой матрицей в левой части, но с разными столбцами свободных коэффициентов. В этом случае b и x являются матрицами. Функция LinearSolve дает решение как в численном, так и в аналитическом виде.

Пример 13.11. Найдем матрицу, обратную к матрице m:

In[ ]: = (m = {{1, 2}, { 2, -1}}; b={{1, 0}, { 0, 1}}; m1 = LinearSolve[m, b]//N)

Out[ ] = {{ 0.2, 0.4}, { 0.4, -0.2}}

Для проверки полученного результата вычислим произведение матриц m и m1:

In[ ]: = m1. m Out[ ] = {{1, 0}, { 0, 1}}

Функция RowReduce[m] – преобразует матрицу m к жордановой форме. Невырожденная матрица преобразуется в единичную матрицу; вырожденная матрица принимает ступенчатый вид.

Пример 13.12. Применим функцию RowReduce к вырожденной матрице:

In[ ]: = m5={{2, 3,1}, {0,2,1}, {2, 5, 2}}; RowReduce[m5]

Out[ ] =

Функция RowReduce позволяет найти решение системы линейных алгебраических уравнений 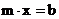. Для решения опишем систему уравнений с помощью расширенной матрицы mb – матрицы m с присоединенным столбцом b (или с присоединенной матрицей b в случае одновременного решения нескольких систем уравнений). Применение к расширенной матрице функции RowReduce реализует процесс решения системы уравнений по схеме Жордана: левая часть матрицы – m – преобразуется в единичную матрицу, в то время как в правой части – b – получаем решение системы.

Пример 13.13. Найдем матрицу, обратную к матрице m = {{1, 2}, {2, -1}}. Для этого присоединим к матрице m единичную матрицу и применим функцию RowReduc:

In[ ]: = RowReduce[{{1, 2, 1, 0}, {2, -1, 0, 1}}]//MatrixForm

Out[ ]/MatrixForm =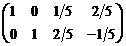

Последние два столбца полученной матрицы представляют матрицу, обратную к матрице m.

Функция Roots[eqn, var] – ищет корни полиномиального уравнения eqn для переменной var. Решение записывается в виде логических равенств, объединенных знаком дизъюнкции – логического “или”.

Пример 13.14.

Найдем корни многочлена Чебышева третьей степени (ChebyshevT[3, x] = -3x + 4x³):

In[ ]: = Roots[ChebyshevT[3, x] == 0, x]

Out[ ] =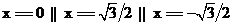

Функция FindRoot[eqn, {x, x₀}] – ищет численное решение уравнения eqn, используя начальное приближение x=x₀.

FindRoot[ {eqn₁, eqn₂, …}, {x, x₀}, {y, y₀}, …] – ищет решениесистемы уравнений. Если все начальные приближения – действительные числа, FindRoot ищет только действительные решения; для поиска комплексных решений необходимо, чтобы хотя бы одно из начальных приближений было комплексным.

Пример 13.15.

In[ ]: = z=FindRoot[Tan[x]==x+1/4,{x,1}] Out[ ] ={x –>0.818503}

Проверка: In[ ]: = Tan[z[[1,2]]] - 1/4 Out[ ] = 0.818503

Отметим, что функция Solve не позволяет найти решение данного уравнения.

13.4. Решение дифференциальных уравнений

DSolve[ eqn, y[x], x ] – решает дифференциальное уравнение для функции y[x].

DSolve[{eqn₁, eqn₂,…}, {y₁[x], y₂[x],…}, x ] – решает систему дифференциальных уравнений.

Пример 13.16.

1). Общее решение.

In[ ]: = DSolve[ y''[x] + y[x] == 0, y[x], x ]

Out[ ] = {{ y[x] –> C[2] Cos[x] – C[1] Sin[x] }}

2). Решение задачи Коши.

In[ ]:= DSolve[{ y''[x] + y[x] == 0, y[0] == 1, y'[0] == 0 }, y[x], x ]

Out[ ] = {{ y[x] –> Cos[x] }}

3). Решение краевой задачи.

In[ ]:= DSolve[{ y''[x] + y[x] == 0, y[0] == 0, y[5Pi / 6] == 1}, y[x], x ]

Out[ ] = {{ y[x] –> 2 Sin[x] }}

4). Решение краевой задачи для системы уравнений.

In[ ]:= DSolve[{ y'[x] == z[x], z'[x] == -y[x], y[0] == 0, z[Pi] == -1}, {y[x], z[x]}, x ]

Out[ ] = {{ y[x] –> Sin[x], z[x] –> Cos[x] }}

NDSolve[ eqns, {y₁, y₂,…}, {x, xmin, xmax}] дает приближенное решение системы дифференциальных уравнений eqns на отрезке [xmin, xmax] для функций y_i[x]. NDSolve представляет решение на данном отрезке в виде интерполирующей функции InterpolatingFunction. Интерполирующая функция позволяет найти значения y для всех x, принадлежащих отрезку интерполяции, и построить график.

Пример 13.17. Найдем решение уравнения колебаний, описывающее затухающую синусоиду:

In[ ]: = s = NDSolve[{ y''[t] + 0.1y'[t] +y[t] == 0, y[0] == 1, y'[0] == 0}, y, {t, 0, 20}]

Out[ ] = {{ y –> InterpolatingFunction[{{ 0., 20. }}, <>]}}

Решение представляется в виде интерполирующей функции. Построим график изменения 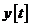и 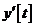, а также “фазовый портрет” – зависимость 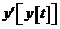. Для построения параментрического графика требуется использовать функцию Evaluate:

In[ ]:= p1=Plot[{y[t]/.s, y'[t]/.s}, {t,0,20}, PlotStyle->{RGBColor[1,0,0],

RGBColor[0,0,1]}, AxesLabel->{t, y}];

p2=ParametricPlot[ Evaluate[{y[t], y'[t]}/.s], {t, 0, 20}, AxesLabel->{y,y'},

PlotStyle->RGBColor[1,0,1]];

Show[GraphicsArray[{p1,p2}]]

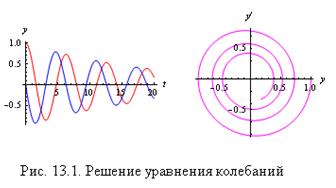Графики показаны на рис. 13.1.

Решение в виде интерполирующей функции позволяет найти значения 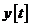и 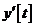в любой точке отрезка, например:

In[ ]: = {y[2Pi] /. s, y'[3Pi/2] /. s} Out[ ] = {{0.730093},{0.791057}}

Замечания

· Дифференциальные уравнения должны иметь достаточное количество начальных или краевых условий.

· Значение x₀, входящее в начальные или краевые условия, может не принадлежать отрезку [xmin, xmax].

· Уравнения могут включать комплексные числа.

 

14. Преобразование выражений

14.1. Стандартная форма выражений

Все объекты, с которыми оперирует Математика, называются выражениями (Expression). Прототипом выражения является f[x,y]. Здесь f является заголовком (Head), а x и y – элементами выражения. В частности это выражение может описывать математическую функцию от двух аргументов f(x,y). В свою очередь x и y также могут быть выражениями.

Понятие выражения служит унифицирующим принципом Математики. То, что все объекты имеют подобную структуру, позволяет строить различные конструкции в разных областях применения с помощью сравнительно малого количества основных операций.

Хотя многие формулы могут быть выражены в разном виде, внутри пакета Математика эти формулы преобразуются в стандартную форму. Эту форму можно вывести на экран с помощью команды FullForm[expr]. Примеры выражений приведены в таблице 14.1. Обратим внимание, что стандартная форма записывается в виде: Заголовок[аргумент1, аргумент2,…], – где заголовок описывает основное действие, объединяющее аргументы.

14.2. Обращение к элементам выражений

К элементам любого выражения можно обращаться точно так же, как к элементам списков, используя команды:

Part[expr, n] или (expr)[[n]] – выделение элемента выражения expr с номером n;

Part[expr, {n1, n2,...}] или (expr)[[{n1, n2,...}]] – выделение списка из нескольких частей выражения. При этом заголовок выражения имеет номер “0”.

К заголовку выражения можно обращаться также с помощью команды Head[expr].

Пример 14.1 Рассмотрим заголовки выражений:

In[ ]: = Head[2] Out[ ] = Integer In[ ]: = “a”[[0]] Out[ ] = String

In[ ]: = Head[2.] Out[ ] = Real In[ ]: = f[x, y][[0]] Out[ ] = f

In[ ]: = Head[2/3] Out[ ] = Rational

14.3. Представление выражения в виде дерева

Любое выражение может быть представлено в виде дерева. Пример приведен на рис. 14.1.

Соответственно, можно говорить о глубине и об уровнях выражения. Команда Depth[expr] – подсчитывает количество уровней в выраженииexpr, а команда Level[epxr, lev] – выводит список частей выражения, стоящих на уровнях, указанных в спецификации lev.

Варианты спецификации уровней:

{n} – только один уровень с номером “n”;

n – все уровни от 1 до n;

Infinity - все уровни;

{-1} – “листья” дерева - концевые узлы.

Например, Depth[h]равно четырем; команда Level[h, {0}] выводит список нулевого уровня, включающий все выражение: {1 + (3 + x)² + y}; команда Level[h, {1}] выводит список всех трех элементов выражения h: {1, (3 + x)², y}; команда Level[h, {3}] выводит список элементов самого нижнего уровня: {3, x}; команда Level[h, {-1}] выводит список концевых узлов: {1, 2, 3, x, y}.

14.4. Операции преобразования выражений

Применение операций преобразования списков.

Приведенные в разделе 9 команды преобразования списков применимы также к любым выражениям. Рассмотрим примеры.

Пример 14.2

Введем выражение: In[ ]: = g = 1 + y + z^2;

Выделим первый подэлемент третьего элемента: In[ ]: = g [[3,1]] Out[ ] = z

Заменим первый подэлемент третьего элемента:

In[ ]: = g [[3,1]]=x+3; g Out[ ] =1 + (3 + x)² + y

Пример 14.3

Введем выражение: In[ ]: = a=E^x Out[ ] =e^x

Добавим к выражению еще один элемент: In[ ]: = b=Append[a, y] Out[ ] =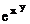

Применим циклическую перестановку: In[ ]: = RotateLeft[b, 1] Out[ ] =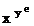

Операции с заголовками выражений.

В выражении типа f[x] имя функции f само является выражением, и с ним можно производить те же действия, что и с другими выражениями.

- Можно изменять имя по правилу замены.

Пример 14.4 In[ ]: = {x, a, 5} /. List -> Plus Out[ ] = 5 + a + x

- Можно присваивать имени новое значение.

Пример 14.5 In[ ]: = f = Sin; {f[x], f[Pi/2]} Out[ ] = {Sin[x], 1}

- Можно использовать имя как аргумент.

Пример 14.6 In[ ]: = g[f_, x_]:= f[x^2]; g[Sin, y] Out[ ] = Sin[y²]

Оператор Apply.

Оператор Apply[f, expr] или f@@expr заменяет заголовок выражения на f. Apply[f, expr, lev] – применяет функцию f на уровне или уровнях, указанных в спецификации lev.

Пример 14.7 Вычисление среднего арифметического.

In[ ]: = mean[list_]:= Apply[Plus, list] / Length[list];

L1 = Table[Random[Integer, {0, 10}], {100}]; mean[L1]//N Out[ ] = 4.79

Применение операторов к частям выражений.

Функциональный оператор Map[f, expr] – применяет функцию f к каждому элементу выражения expr.

Пример 14.8 In[ ]: = Map[Cos, {a, b, Pi}] Out[ ] = {Cos[a], Cos[b], -1}

Оператор Map[f, expr, lev] – применяет функцию f к каждому элементу выражения expr на уровне, определяемом спецификацией lev.

Пример 14.9 Создадим простое выражение e1=a/b. С помощью команды Level выделим в этом выражении элементы, стоящие на первом уровне, а затем применим к ним функцию Sin. Аналогично выделим элементы второго уровня и применим к ним ту же функцию Sin. Наконец, применим функцию Sin ко всем уровням выражения e1 от первого до второго.

In[ ]: = {e1=a/b; Level[e1, {1}], Map[Sin, e1], Level[e1, {2}], Map[Sin, e1, {2}], Map[Sin, e1, 2]}

Out[ ] = {{a, 1/b}, Sin[a] Sin[1/b], {b, -1}, a Sin[b]^-Sin[1], Sin[a] Sin[Sin[b]^-Sin[1]]}

14.5. Повторное выполнение операций

Некоторые из функциональных операторов предназначены для циклической обработки выражений. Применение таких операторов часто позволяет записать итерационный процесс короче, чем с помощью обычных циклических операций.

Оператор NestList[f, expr, n] – выдаетсписок, который включает исходное выражение expr и результаты n-кратного применения к этому выражению функции f. Функция Nest[f, expr, n] – выдает только последний элемент этого списка.

Пример 14.10

In[ ]: = NestList[f, x, 3] Out[ ] = {x, f[x], f[f[x]], f[f[f[x]]]}

Пример 14.11

Составим программу для решения методом Эйлера задачи Коши для дифференциального уравнения y’(x) = f(x, y) c начальным условием y(x₀) = y₀. Введем на оси x сетку: x_i = x₀ + h*i, где h – шаг приращения аргумента x. В соответствии с методом Эйлера формула для последовательного вычисления значений y в узлах сетки имеет вид: y_i+1 = y_i + h*f(x_i, y_i).

In[ ]: = E2[f_, x0_, y0_, h_, n_]:= Module[{w},

w[{x_, y_}] = {x+h, y+h*f[x, y]}; NestList[w, {x0, y0}, n]]

Обратим внимание, что функция w является векторной функцией.

Найдем решение уравнения y’(x) = y с начальным условием y(0)=1:

In[ ]: = f[x_, y_] = y; E2[f, 0, 1, 0.05, 3]

Out[ ] = {{0, 1}, {0.05, 1.05}, {0.1, 1.1025}, {0.15, 1.15763}}

Элементы этого списка содержат значения x и y в узлах сетки с шагом 0.05. Точное решение данной задачи Коши представляет собой экспоненту: y(x) = e^x. Сравним найденное приближенное решение с точным:

In[ ]: = Table[{x, Exp[x]}, {x, 0, 0.15, 0.05}]

Out[ ] = {{0, 1}, {0.05, 1.05127}, {0.1, 1.10517}, {0.15, 1.16183}}

Оператор FixedPointList[f, expr] – генерирует список результатов повторного применения функции f к выражению expr. Список начинается с выражения expr и заканчивается, когда результаты повторного применения f перестают изменяться (в пределах точности, обеспечиваемой компьютером). FixedPoint[f, expr] – выдает только последний элемент списка.

Пример 14.12

Создадим функцию для вычисления квадратного корня числа x с помощью итерационного процесса Герона (один из вариантов такой функции приведен в разделе 8, пример 8.10):

In[ ]: = r2[x_]:= Module[{f}, f[v_] = (v+ x / v) / 2; FixedPoint[f, x+1.]]

В программе задается начальное значение x+1, которое затем уточняется в процессе последовательных итераций – повторном применении функции f. Например, найдем значение квадратного корня из двух:

In[ ]: = r2[2] Out[ ] = 1.41421

Оператор NestWhileList[f, x, test] – генерирует список {x, f[x], f[f[x]], …}; процесс генерации заканчивается, когда перестает выполняться условие test.

NestWhileList[f, x, test, m] – в качестве аргументов условия test используются m последних результатов применения функции f.

NestWhile[…] – выдает только последний элемент списка.

14.6. Анонимные функции

Анонимные функции – это функции без имени. В ряде случаев функции вводятся только для однократного использования. Например, таковы локальные функции, входящие в конструкцию Module. Если функция используется только один раз, то она и не нуждается в имени. Синтаксис анонимной функции: body &, – тело функции, заканчивающееся знаком амперсенд &. Формальными аргументами анонимной функции служат # или #1, #2, #3, … Знак & является обязательным элементом, указывающим, что данное выражение является определением анонимной функции. Амперсенд имеет самый низкий приоритет, поэтому в выражениях типа #1+#2 & тело функции не требуется заключать в скобки. С другой стороны, если анонимная функция служит правой частью выражения, то вся она должна быть взята в скобки, например: option -> (body &).

Пример 14.13

Запишем выражение, содержащее два вхождения функции Sin, а затем заменим в этом выражении Sin на возведение в квадрат:

In[ ]: = {b = Sin[a + Sin[2x]], b/.Sin->(#^2 &)} Out[ ] = {Sin[a = Sin[2x]], (a + 4 x²)²}

Использование анонимных функций совместно с операциями циклической обработки выражений позволяет создавать очень компактные программы.

Пример14.14

Вычисление квадратного корня с помощью процесса Герона (см. примеры 8.10, 14.12):

In[ ]: = r3[x_]:= FixedPoint[(# + x / #) / 2 &, x+1.]; r3[2] Out[ ] = 1.41421

 

Пример14.15

Нахождение корня уравнения f(x)= 0 с помощью итерационного метода Ньютона. Алгоритм Ньютона описывается формулой: x_i+1 = x_i – f(x_i) / f’(x_i), где x_i – значение корня, полученное на i-ом шаге итераций. Задав подходящее начальное значение x₀, можно найти значение корня с требуемой точностью. Опишем алгоритм Ньютона с использованием циклической операции FixedPoint:

In[ ]: = Newt[f_, x0_]:= FixedPoint[# - f[#] / f’[#] &, x0]

Здесь x0 – начальное приближение. Данная программа позволяет найти корень уравнения уравнения f(x)= 0 с точностью, которую обеспечивает математический сопроцессор.

Использование циклической операции NestWhile позволяет найти корень уравнения с заданной точностью:

In[ ]: = Newt2[f_, x0_, eps_]:= NestWhile[# - f[#] / f’[#] &, x0, Abs[#1 - #2] > eps &, 2]

Итерационный процесс, описываемый данной программой, заканчивается, если два последних значения отличаются не более, чем на eps.

Найдем положительный корень уравнения x³+x- 1 = 0с точностью 10^-5:

In[ ]: = f [x_] = x^3+x-1.; Newt2[f, 1., 10^-5] Out[ ] = 0.682328

Пример14.16

Вычисление “машинного эпсилон” (см. также примеры 7.1 и 7.2):

In[ ]: = NestWhile[# / 2. &, 1., # + 1. > 1. &]*2 Out[ ] = 2.84212*10^-14

14.7. Функциональные операторы Outer и Inner

Функциональный оператор Outer[f, list₁, list₂] называют обобщенным произведением. Оператор применяет функцию f ко всем сочетаниям элементов списков list₁, list₂.

Пример14.17

In[ ]: = Outer[f, {a, b}, {1, 2}] Out[ ] = {{f[a, 1], f[a, 2]}, {f[b, 1], f[b, 2]}}

Пример14.18

Вычисление матрицы частных производных.

In[ ]: = (jac[f_List, v_List]:= Outer[D, f, v];

fun = {x^2 + 3 y, Sin[x] – Cos[y]}; var = {x, y}; jac[fun, var])

Out[ ] = {{2 x, 3}, {Cos[x], Sin[y]}}

Оператор Inner[f, list₁, list₂, g] в отличие от оператора Outer составляет сочетания элементов, стоящих на одинаковых местах в списках list₁, list₂. К этим сочетаниям оператор применяет функцию f, а затем к списку результатов применяет функцию g, либо просто суммирует результаты, если функция g не указана.

Пример14.19

In[ ]: = Inner[Plus, {a, b}, {1, 2}, Times] Out[ ] = (1 + a) (2 + b)

Пример14.20 Найдем скалярное произведение двух векторов:

In[ ]: = Inner[Times, {a, b}, {c, d}] Out[ ] = a c + b d

Вопросы

1. Основные части пакета Математика.

2. Точные и приближенные вычисления.

3. Операции с ячейками: объединение и разделение ячеек, группирование ячеек. Скрытие содержания группы ячеек.

4. Глобальный характер данных в течение сеанса работы в пакете Математика. Обращение к ячейкам. Удаление данных.

5. Правила написания. Малые и большие буквы. Запись операции умножения. Употребление скобок.

6. Наиболее часто употребляемые операции и функции. Тригонометрические функции. Экспоненциальная функция и логарифм. Вычисление пределов. Правило преобразования. Функция замещения. Вычисление производных. Численное и аналитическое интегрирование. Нахождение минимумов и максимумов. Циклические операции суммирования и умножения. Функция Fit. Функция Print. Получение информации о функциях.

7. Стандартная, префиксная и постфиксная формы обращения к функциям. Приоритеты обращений.

8. Циклические операции: For, While и Do. Логические операторы. Функция If.

9. Функции пользователя. Операции немедленного и задержанного присваивания. Шаблоны для описания типов аргументов.

10. Альтернативные определения функций на разных отрезках значения аргумента. Функция Which.

11. Составление программ. Конструкция Module.

12. Понятие списка. Простой способ определения списка. Функции Range и Table. Операции с элементами списков. Определение векторной функции. Матричные функции.

13. Массивы.

14. Графики. Создание двумерного графика Plot. Основные опции графиков. Установление одинакового масштаба по осям координат. Другие типы графиков: ListPlot, PolarPlot, параметрические графики, трехмерные графики. Функция Show. Массив графиков.

15. Функция Manipulate.

16. Аналитические операции: Series, Expand, Simplify и др.

17. Решение уравнений. Функции: Solve, LinearSolve, Roots, FindRoot.

18. Решение дифференциальных уравнений. Функции: DSolve, NDSolve.

19. Преобразование выражений. Представление выражений в разной форме: FullForm, TreeForm. Уровни выражения. Операции с элементами выражений. Операции с заголовками выражений.

20. Функциональные операторы: Apply, Map. Повторное выполнение операций; операторы:

NestList, FixedPointList, NestWhileList.

21. Анонимные функции. Применение анонимных функций совместно с циклической обработкой выражений.

22. Оператор Outer.