

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Таблица 2
| функция | производная | ||
1. 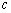
| 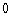
| ||
2. 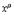
| 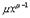
| ||
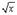
| 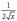
| ||
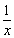
| 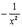
| ||
3. 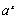
| 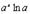
| ||
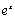
| 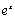
| ||
4. 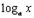
| 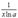
| ||
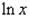
| 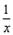
| ||
5. 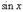
| 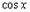
| ||
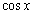
| 
| ||
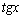
| 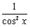
| ||
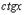
| 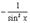
| ||
| функция | производная | ||
6. 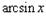
| 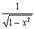
| ||
| 7. arccos x | 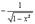
| ||
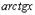
| 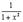
| ||
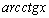
| 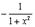
| ||
8. 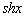
| 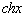
| ||
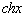
| 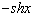
| ||
9. 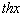
| 
| ||
Особые случаи
То, что в точке  функция
функция  непрерывна не означает, разумеется, что в этой точке у нее обязательно существует производная. Функция может быть непрерывной, а производной может и не существовать. Что же там может быть?
непрерывна не означает, разумеется, что в этой точке у нее обязательно существует производная. Функция может быть непрерывной, а производной может и не существовать. Что же там может быть?
1. А. Односторонние производные
Назовем

производной от функции  в точке
в точке  слева, а
слева, а
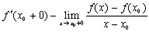
производной в той же точке справа. Разумеется, если  , то это означает, что в точке
, то это означает, что в точке  существует
существует  . Но могут быть случаи, когда
. Но могут быть случаи, когда 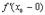 и
и  существуют, но не равны друг другу. В этом случае не существует и
существуют, но не равны друг другу. В этом случае не существует и  . График функции
. График функции  имеет в точке
имеет в точке  в этом случае “излом”, и в этой точке к графику можно провести две касательные.
в этом случае “излом”, и в этой точке к графику можно провести две касательные.

2. Б. Бесконечная производная
Рассмотрим функцию  определенную для
определенную для  и потребуем найти
и потребуем найти  . Имеем
. Имеем

и производная равна  .
.
Рассматривая график функции  легко увидеть, что это означает просто то, что в точке
легко увидеть, что это означает просто то, что в точке  касательная к графику параллельна оси OY.
касательная к графику параллельна оси OY.

3. В. Несуществование производной
Наконец, может быть ситуация, когда  , фигурирующий в определении производной, не существует.
, фигурирующий в определении производной, не существует.
Рассмотрим для примера,  . Так как
. Так как  , то
, то  . Поэтому полагая
. Поэтому полагая  получим
получим


и этот предел просто не существует.
Из графика функции  видно, что с приближением к точке
видно, что с приближением к точке  касательная колеблется, не стремясь ни к какому определенному положению.
касательная колеблется, не стремясь ни к какому определенному положению.
В математике построены даже примеры функций, которые являются непрерывными, но ни в одной точке не имеют производной.
Теоремы Ферма и Ролля
Теорема Ферма. Пусть функция  определена и непрерывна на промежутке
определена и непрерывна на промежутке  и в некоторой внутренней точке
и в некоторой внутренней точке  этого промежутка достигает своего наибольшего или наименьшего значения, если в этой точке существует производная, то она равна нулю:
этого промежутка достигает своего наибольшего или наименьшего значения, если в этой точке существует производная, то она равна нулю:  .
.
|
|
Доказательство
Пусть, для определенности, в точке  функция
функция  достигает своего наибольшего.
достигает своего наибольшего.
По условию теоремы эта точка внутренняя, т.е.  , и поэтому к этой точке можно подойти и слева и справа.
, и поэтому к этой точке можно подойти и слева и справа.
Пусть мы подходим к  слева. Тогда
слева. Тогда
 (т.к.
(т.к. 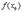 - наибольшее значение)
- наибольшее значение)

 (т.к. мы подходим слева)
(т.к. мы подходим слева)


Делая предельный переход  получим
получим

Пусть мы подходим к точке  справа. Тогда
справа. Тогда
 (т.к.
(т.к. 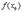 - наибольшее значение)
- наибольшее значение)

 (т.к. мы подходим слева)
(т.к. мы подходим слева)

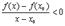
Делая предельный переход  получим
получим
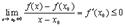
Совместить два полученных неравенства можно только в одном случае:  . ч.т.д.
. ч.т.д.
Геометрический смысл доказанной теоремы ясен из рисунка: в точке наибольшего или наименьшего значения функции касательная к графику функции параллельна оси OX.

1. Существование ограничений
В теореме Ферма по сути дела два ограничения: а) точка  расположена внутри отрезка
расположена внутри отрезка  и б)
и б)  . Покажем, что оба ограничения являются существенными, т.е. отказ от любого из них приводит к тому, что утверждение теоремы становится неверным.
. Покажем, что оба ограничения являются существенными, т.е. отказ от любого из них приводит к тому, что утверждение теоремы становится неверным.
а) “внутренность” точки x0

Если максимум или минимум функции  достигается на границе отрезка, то утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке
достигается на границе отрезка, то утверждение теоремы Ферма неверно. При доказательстве это проявляется в том, что мы сможем подойти к точке  только с одной стороны и поэтому не получится второго, противоположного неравенства.
только с одной стороны и поэтому не получится второго, противоположного неравенства.
б) существование производной.
Пусть в точке  существуют только односторонние производные. Тогда, как это видно из рисунка, теорема Ферма неверна. При доказательстве это проявиться в том, что получаться неравенства
существуют только односторонние производные. Тогда, как это видно из рисунка, теорема Ферма неверна. При доказательстве это проявиться в том, что получаться неравенства  и
и  , которые нельзя будет объединить в одно равенство, т.к. теперь
, которые нельзя будет объединить в одно равенство, т.к. теперь 

Теорема Ролля. Пусть функция 
а) определена и непрерывна на [a,b]
б)  ;
;
в) 
Тогда существует точка  в которой
в которой  .
.
Доказательство этой теоремы следует из такой логической цепочки рассуждений:
|
|
1. Так как  определена и непрерывна на
определена и непрерывна на  , то, по первой теореме Вейерштрасса, она ограничена на
, то, по первой теореме Вейерштрасса, она ограничена на  , т.е. существуют конечные
, т.е. существуют конечные  и
и 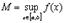 .
.
2. Если 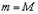 , то
, то 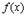 есть константа, т.е.
есть константа, т.е.  и поэтому
и поэтому 
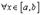 . В качестве точки c можно взять любую точку из
. В качестве точки c можно взять любую точку из  .
.
3. Если  , то, в силу условия
, то, в силу условия  и второй теоремы Вейерштрасса, хотя бы одно из значений
и второй теоремы Вейерштрасса, хотя бы одно из значений  или
или 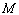 достигается во внутренней точке промежутка
достигается во внутренней точке промежутка  ,по теореме Ферма, в этой точке (их может быть и две) производная равна нулю.
,по теореме Ферма, в этой точке (их может быть и две) производная равна нулю.
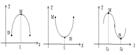
ч.т.д.
Формулы Коши и Лагранжа
Теорема. Пусть функции 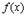 и
и 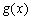
а) определены и непрерывны на  ;
;
б) 
 и
и 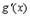 ;
;
в) 

Тогда существует точка  такая, что
такая, что
 .
.
Эта формула носит название формулы Коши.
Доказательство. Прежде всего отметим, что  , иначе, по Теореме Ролля, существовала бы точка
, иначе, по Теореме Ролля, существовала бы точка  , где
, где  , что противоречит ограничению “в”.
, что противоречит ограничению “в”.
Рассмотрим функцию

Она
а) определена и непрерывна на 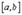 , т.к.
, т.к. 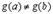 и функции
и функции  и
и  непрерывны на
непрерывны на 
б) 
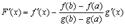
в) 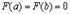
Таким образом, для  выполнены все условия Теоремы Ролля. Поэтому
выполнены все условия Теоремы Ролля. Поэтому 
 такая, что
такая, что
 ,
,
но тогда в этой точке 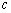
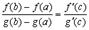
что и дает формулу Коши.
1. Формула Лагранжа
Рассмотри частный случай, когда  . Тогда формула Коши приобретает вид
. Тогда формула Коши приобретает вид

или

где  . Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.
. Эта формула и называется формулой Лагранжа. В дальнейшем мы будем на нее часто ссылаться.
Заметим, что точка c не обязательно единственная: может быть несколько точек c, удовлетворяющих формулам Коши или Лагранжа.
Рассмотрим еще вопрос о геометрическом смысле формулы Лагранжа. Пусть мы имеем график  . Проведем через точки
. Проведем через точки  и
и  секущую. Она образует с осью OX угол
секущую. Она образует с осью OX угол 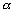 и
и  . Но
. Но  есть тангенс угла, который касательная к кривой в точке
есть тангенс угла, который касательная к кривой в точке  образует с осью OX. Поэтому формулу Лагранжа можно трактовать так: существует точка
образует с осью OX. Поэтому формулу Лагранжа можно трактовать так: существует точка  , касательная в которой параллельна секущей, соединяющей точки
, касательная в которой параллельна секущей, соединяющей точки 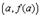 и
и  .
.

Дифференциал
Рассмотрим важное для дальнейшего понятие дифференциала.
Напомним, что величина  называется приращением функции.
называется приращением функции.
Определение 1. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее приращение можно представить в виде
, если ее приращение можно представить в виде

Определение 2. Линейная часть приращения функции, т.е.  называется дифференциалом функции
называется дифференциалом функции  и обозначается
и обозначается 

Чтобы точно уяснить эти определения функции рассмотрим пример. Пусть  . Тогда
. Тогда

Заметим, что  содержит слагаемое, линейное по
содержит слагаемое, линейное по  , слагаемые с
, слагаемые с 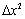 и
и 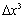 . Так вот, только слагаемое, линейное по
. Так вот, только слагаемое, линейное по  дает дифференциал, т.е.
дает дифференциал, т.е.
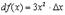
1. Теорема о дифференцируемости функций
|
|
Для того, чтобы функция  была дифференцируемой в точке
была дифференцируемой в точке  , необходимо и достаточно, чтобы в этой точке существовала производная
, необходимо и достаточно, чтобы в этой точке существовала производная 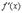 . При этом
. При этом  .
.
Доказательство
Необходимость. Пусть 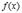 дифференцируема в точке
дифференцируема в точке  . Это значит, что
. Это значит, что

Деля на 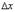
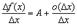
и переходя к пределу 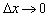 , получим
, получим
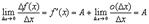
Достаточность. Пусть в точке  существует производная
существует производная
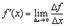
Это, по определению, означает, что
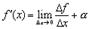
где 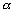 - бесконечно малая величина. Отсюда следует, что
- бесконечно малая величина. Отсюда следует, что
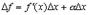
Но 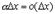 и поэтому
и поэтому

что и требовалось доказать.
2. Выражение для дифференциала
Итак, мы получили, что для дифференцируемой функции 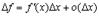 . Это означает, что
. Это означает, что
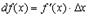 .
.
Но если взять 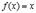 , то мы получим, что
, то мы получим, что 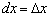 , т.е. дифференциал независимой переменной равен ее приращению. Поэтому окончательно
, т.е. дифференциал независимой переменной равен ее приращению. Поэтому окончательно

Отсюда следует, что
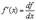
т.е. производная есть отношение дифференциала функции к дифференциалу независимой переменной. Заметьте, что 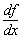 есть обычная дробь и с ней можно обращаться как с обычной дробью.
есть обычная дробь и с ней можно обращаться как с обычной дробью.
3. Геометрический смысл дифференциала
Вспомним, что  есть тангенс угла наклона касательной к оси OX. Поэтому, если провести касательную к кривой в точке
есть тангенс угла наклона касательной к оси OX. Поэтому, если провести касательную к кривой в точке  , то
, то 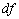 будет катетом, который противолежит углу
будет катетом, который противолежит углу 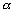 в треугольнике, гипотенуза которого образована касательной, а другой катет есть приращение
в треугольнике, гипотенуза которого образована касательной, а другой катет есть приращение  На рисунке нарисован и отрезок
На рисунке нарисован и отрезок 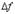 , так что видно отличие
, так что видно отличие 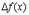 и
и 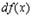 .
.

Правила дифференцирования
Пользуясь формулой 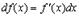 выведем несколько важных формул, касающихся дифференциалов.
выведем несколько важных формул, касающихся дифференциалов.
1. 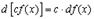
Действительно
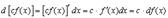
2. 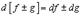
Имеем
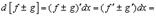
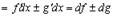
3. 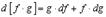
Имеем
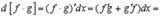
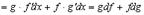
4. 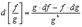
Имеем
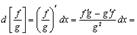
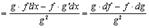 .
.
5. 
Имеем
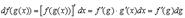
В качестве приложения понятия дифференциала выведем формулу для производной от функций заданных параметрически.
Параметрическое задание функции заключается в том, что и  и
и 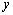 задаются как функции некоторого параметра
задаются как функции некоторого параметра 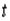 , т.е.
, т.е.
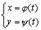 ,
, 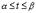
Значение параметра 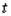 определяет одновременно и
определяет одновременно и  и
и 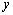 , и, тем самым, некоторую точку на плоскости. Меняя
, и, тем самым, некоторую точку на плоскости. Меняя 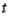 мы двигаем точку на плоскости и она описывает некоторую кривую, определяющую зависимость
мы двигаем точку на плоскости и она описывает некоторую кривую, определяющую зависимость 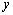 от
от  . Параметрическое задание функции считается самым общим способом задания кривых на плоскости.
. Параметрическое задание функции считается самым общим способом задания кривых на плоскости.
Имеем
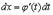
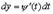
Отсюда производная от 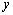 по
по  имеет вид
имеет вид


Сокращая на 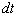 получим окончательно
получим окончательно
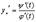
Производные и дифференциалы высших порядков.
|
|
Пусть имеется функция 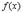 , от которой мы вычислили первую производную
, от которой мы вычислили первую производную 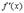 . Но
. Но  снова является функцией и от нее можно тоже вычислить производную. Производная от первой производной т.е.
снова является функцией и от нее можно тоже вычислить производную. Производная от первой производной т.е. 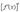 называется второй производной и обозначается
называется второй производной и обозначается 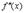 :
:
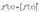
Аналогично, производная от второй производной называется третьей производной
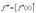 .
.
Аналогично определяются производные более высоких порядков. Отметим только, что производные более высоких порядков отмечаются не штрихами (их было бы слишком много) а цифрами, заключенными в скобки - 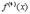 ,
, 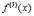 и т.д.
и т.д.
Итак, производная n-го порядка определяется как производная от производной (n-1)-го порядка
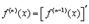
Основные формулы, касающиеся производных высших порядков, следующие:
1. 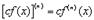
2. 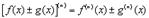
3. 
Первые две формулы очевидны. Третью формулу, носящую название формулы Лейбница, мы доказывать не будем. При ее применении следует только иметь ввиду, что производной нулевого порядка считается сама функция, т.е. 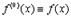 .
.
Аналогично этому, дифференциалом второго порядка называется дифференциал от первого дифференциала, т.е.
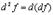
Выведем формулу для 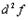 . Имеем
. Имеем
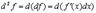
При дальнейшем преобразовании следует иметь в виду, чтоdx, совпадающее с приращением аргументаdx, есть величина, совершенно не зависимая от  , т.к. мы
, т.к. мы 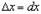 можем взять каким угодно. Поэтому по отношению к x dx
можем взять каким угодно. Поэтому по отношению к x dx
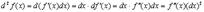 .
.
Скобки у 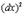 обычно не пишут
обычно не пишут
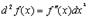
Отсюда
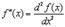
Аналогично, дифференциал третьего порядка определяется как дифференциал от второго дифференциала
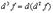
Имеем
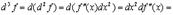
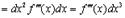
так что
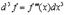 ;
; 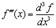
В общем случае
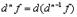
Легко показывается по индукции, что
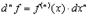 ;
; 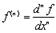 .
.
|
|
|

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!