Линейного программирования
Если число переменных в общей задаче линейного программирования равно двум или трем, то такая задача имеет особенно простое геометрическое истолкование и, соответственно, ее решение может быть получено геометрическим методом. Для конкретности рассмотрим следующую задачу ЛП:
f(X) = c1x1 + c2x2  max
max
a11x1 + a12x2  b1
b1
a21x1 + a22x2  b2
b2
…………………. (4)
am1x1 + am2x2  bm
bm
x1  0, x2
0, x2  0
0
Каждому из ограничений задачи (4) соответствует полуплоскость, а в совокупности они представляют на плоскости O x1x2 многоугольник (или пустое множество). Геометрически, с учетом ограничений на знак переменных x1 и x2, имеем следующую картину:
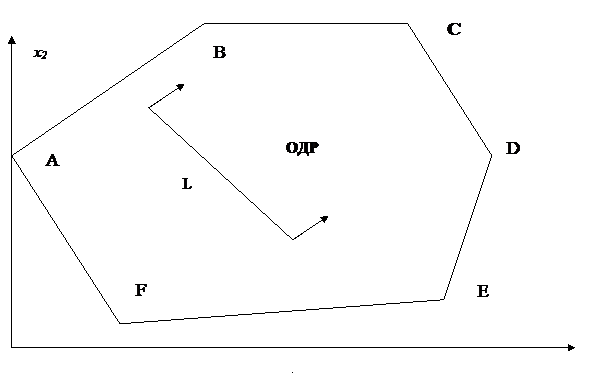
Рис. 1.
Область допустимых решений (ОДР) – это область внутри шестиугольника ABCDEF. Фиксированным значениям целевой функции f(X) соответствует фиксированное положение прямой L (уравнение прямой L: c1x1 + c2x2 = d, где d фиксированное значение), возрастание f(X) соответствует движению прямой L в направлении, указанном стрелками. Когда прямая L занимает положение, соответствующее ее прохождению через точку C ( точка C выделена жирно – это одна из вершин шестиугольника ), целевая функция достигает своего наибольшего значения. Таким образом, решением задачи ЛП будет x1 = x1c, x2 = x2c, а f(Xопт) = f(Xc), где x1c, x2c – координаты точки C.
Пример. Решить следующую задачу линейного программирования:
2x + y  max
max
x + y  1,
1,
x + 2y  6,
6,
y  2,
2,
x 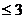 ,
,
(x  0, y
0, y  0).
0).
Здесь для удобства студентов выбраны более привычные для них переменные x и y. Область допустимых решений изображена на Рис. 2:
Рис. 2.
Она представляет собой многоугольник ABCDEF (здесь уравнение прямой BC: y = 2, CD: x + 2y = 6, DE: x = 3, EF: y = 0, AF: x + y =1,AB: x = 0). Прямая L соответствует уравнению целевой функции: 2x + y = d, где d – параметр. Очевидно, что целевая функция будет достигать максимума в ОДР, когда прямая L будет проходить через точку D. Точка D это точка пересечения прямых CD и DE, решая совместно систему уравнений:
x + 2y = 6,
x = 3,
получим координаты точки D: x = 3, y = 3/2. Таким образом, решением данной задачи будет x = 3, y = 3/2, значение целевой функции при этом будет f(Xопт) = 4 + 3/2 = 11/2.
Таблица и алгоритм решения канонических задач линейного
Программирования симплекс – методом
Каноническую задачу ЛП можно записать в виде таблицы:
| Базисные
переменные
| Свободные
члены
| x1
| x2
| …
| xk
| xk+1
| xk+2
| …
| xn
|
| xk+1
| b1
| a11
| a1
| …
| a1k
| 1
| 0
| …
| 0
|
| xk+2
| b2
| a21
| a22
| …
| a2k
| 0
| 1
| …
| 0
|
| …
| …
| ...
| …
| …
| …
| …
| …
| …
| …
|
| xk+r
| br
| ar1
| ar2
| …
| ark
| 0
| 0
| …
| 1
|
| f(X)
| c0
| c1
| c2
| …
| ck
| 0
| 0
| …
| 0
|
Начальный базисный план задачи получается из этой таблицы и имеет вид вектора
Xb = (0,0,…, 0,b1,b2, …,br)т, то-есть x1b=0,x2b=0,…,xkb=0,xk+1b=b1,xk+2b=b2, …,xnb=br.
Описываемый ниже алгоритм решения канонической задачи ЛП основан на этой таблице.
Схема алгоритма 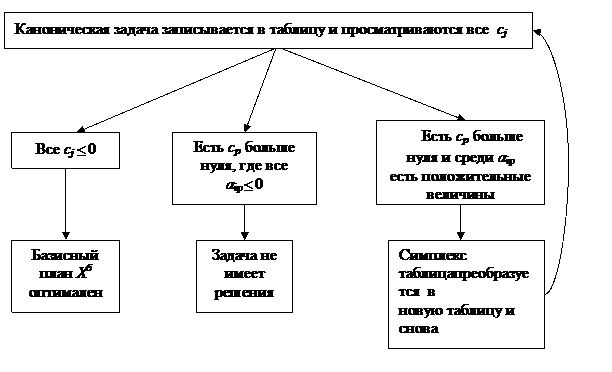
Рис. 3.
Рассмотрим подробнее последний блок алгоритма о преобразовании таблиц. По условию, в этом случае в столбце таблицы, соответствующему положительному элементу cp, есть положительные элементы a ip; для каждого из этих элементов находим отношение b i/ a ip и находим наименьшее из этих отношений, пусть оно соответствует элементу a kp, это означает, что таблицу нужно преобразовывать, переводя переменную xk из базисных переменных в свободные переменные, а переменную xp наоборот переводят из свободных переменных в базисные; делается это следующим образом: сначала преобразуется k –тая строка таблицы – путем деления всех элементов этой строки на a kp - результаты заносятся в k – тую строку новой таблицы, затем по формулам метода Гаусса для систем линейных алгебраических уравнений преобразуются остальные элементы таблицы (табличный вариант этого метода носит название «правила двух перпендикуляров» и оно состоит в том, что элемент новой таблицы получается путем вычитания из соответствующего элемента старой таблицы произведения элементов, стоящих на концах перпендикуляров, проведенных от старого элемента на p – тый столбец и на уже полученную k - тую строку новой таблицы). Рассмотрим пример.
Пример.
f(X)= - 3x4 + 8x5 + 2x6 + 15  min
min
x1 – 2x4 + 3x5 – 7x6 = 12;
x2 + 2x4 + x5 – 3x6 = 8;
x3 + x4 + 4x5 – 5x6 = 7;
xj  0; j = 1, 2, 3, 4, 5, 6.
0; j = 1, 2, 3, 4, 5, 6.
Задача является канонической, переменные x1, x2, x3 – базисные переменные, остальные переменные x4, x5, x6 – свободные. Заполняем исходную симплекс – таблицу:
| Базисные
переменные
| Свободные
члены
| x1
| x2
| x3
| x4
| x5
| x6
|
| x1
| 12
| 1
| 0
| 0
| -2
| 3
| -7
|
| x2
| 8
| 0
| 1
| 0
|
| 1
| -3
|
| x3
| 7
| 0
| 0
| 1
|
| 4
| -5
|
| f(X)
| 15
| 0
| 0
| 0
|
| -8
| -2
|
| x1
| 20
| 1
| 1
| 0
| 0
| 4
| -10
|
| x4
|
|
| 1/2
|
| 1
| 1/2
| -3/2
|
| x3
| 3
| 0
| -1/2
| 1
| 0
| 7/2
| -7/2
|
| f(X)
| 3
| 0
| -3/2
| 0
| 0
| -19/2
| 5/2
|
В строке для f(X) среди элементов c1, c2, …, c6 есть только один положительный элемент c4 = 3, а в столбце над этим элементом (столбец выделен жирным шрифтом) есть два положительных элемента (1 и 2). Вычисляем для этих двух элементов отношения b i/ aip, получаем 8/2 = 4, 7/1 = 7. Наименьшим из чисел 4 и 7 является 4, это число соответствует элементу a 24 =2, стоящем в строке таблицы, соответствующей базисной переменной x2. Это означает, что переменная x2 из базисных переменных перейдет в разряд свободных, а на ее место в разряд базисных придет переменная x4, что и отражено в первом столбце следующей части таблицы. Преобразование таблицы начинается со старой строки для x2: все элементы этой строки делятся на число a 24 =2 и результат заносится в строку для x4 новой части таблицы (эта строка выделена жирным шрифтом). Дальнейшие преобразования таблицы осуществляются по правилу двух перпендикуляров (строка и столбец, на которые нужно опускать перпендикуляры, выделены жирным шрифтом). Например, первый элемент, стоящий в строке для x1 (а там стоит число 12), получается по формуле 12 – 4(-2) = 20, потому что на концах перпендикуляров, опущенных из ячейки для числа 12 на выделенные жирным шрифтом строку и столбец, стоят числа 4 и (-2). Число 20 записывается в соответствующую ячейку новой части таблицы и так пересчитываются все остальные элементы старой части таблицы. После преобразования таблицы снова смотрим на строчку для f(X), среди элементов c j этой строки есть положительный элемент c6 = 5/2, а в столбце над этим элементом нет положительных элементов. В соответствии с алгоритмом, получаем, что задача не имеет решения в силу неограниченности целевой функции.
Метод искусственного базиса
Как уже отмечалось, основная задача не всегда может быть приведена к канонической, даже, если она может быть приведена к канонической, это приведение может быть не очевидным. Поэтому для этой цели применяется метод искусственного базиса. Этот метод состоит в следующем. Кроме исходной основной задачи формулируется вспомогательная задача, которая всегда имеет решение, и по решению вспомогательной задачи делается вывод, либо о том, что исходная задача имеет допустимый план и далее эта задача решается симплекс – методом, либо о том, что исходная основная задача не имеет решения. Рассмотрим этот процесс более подробно.
Пусть исходная основная задача формулируется в следующем виде:
f(X) = c1x1 + c2x2 + … + cnxn  min
min
a11x1 + a12x2 + … + a1nxn = b1
a21x1 + a22x2 + … + a2nxn = b2
……………………………… (A)
am1x1 + am2x2 + … + amnxn = bm
(x1  0, x2
0, x2  0, …, xn
0, …, xn  0).
0).
Примечание: Если в ограничениях задачи (А) среди свободных членов bj есть отрицательные, то в соответствующем уравнении нужно изменить на противоположный знаки в правой и левой частях, чтобы справа стоял положительный элемент.
Введем новые дополнительные переменные xn+1, xn+2, …, xn+m, число которых равно числу ограничений задачи (A), и сформулируем новую вспомогательную задачу в виде:
g(X) = xn+1 + xn+2 + … + xn+m  min
min
a11x1 + a12x2 + … + a1nxn + xn+1 = b1
a21x1 + a22x2 + … + a2nxn + xn+2 = b2
……………………………………… (B)
am1x1 + am2x2 + … + amnxn + xn+m = bm
(x1  0, x2
0, x2  0, …, xn
0, …, xn  0, xn+1
0, xn+1  0, …, xn+m
0, …, xn+m  0).
0).
Несколько слов по поводу формулирования задачи (B): целевая функция задачи (В) взята в виде суммы новых дополнительных переменных, а ограничения задачи (В) получены из ограничений задачи (А) путем прибавления к каждому уравнению (в левой части уравнения) по одной дополнительной переменной. Задача (В) становится канонической, если в целевой функции этой задачи с помощью ограничений этой задачи выразить базисные переменные xn+1, xn+2, …, xn+m через свободные переменные x1, x2, …, xn. Поэтому, как каноническая задача, задача (В) всегда имеет решение. Ее исходный базисный план имеет вид: x1 = 0, x2 = 0, …, xn = 0, xn+1 = b1, xn+2 = bm.
По поводу взаимосвязи решений задач (А) и (В) доказаны определенные теоремы, которые позволяют сформулировать нижеследующий алгоритм перехода от задачи (В) к исходной задаче (А):
| Таблица задачи (В) преобразуется в таблицу задачи (А) и осуществляется решение задачи (А)
| |

Рис. 4.
Пример. Решить следующую задачу линейного программирования
f(X) = 3x1 + x2  max
max
x1 + x2 + x3 = 8
x1 – x3 = 5 (А)
x1, x2, x3  0.
0.
Задача (А) не является основной, так как целевая функция в ней на максимум, а должна быть на минимум. Поэтому заменим целевую функцию на противоположную по знаку, тогда получим
f1(X) = -3x1 – x2  min (*)
min (*)
Составим для задачи (А) вспомогательную задачу (В), для этого включим в ограничения задачи (А) искусственные переменные x4 и x5, а целевую функцию возьмем, как сумму этих переменных g(X) = x4 + x5,
тогда получим следующую задачу (В):
g(X) = 13 – 2x1 – x2  min
min
x1 + x2 + x3 + x4 = 8
x1 – x3 + x5 = 5 (В)
xj  0.
0.
Здесь целевая функция g(X) выражена через свободные переменные x1, x2 (с помощью ограничений задачи (В)).
Составим симплекс – таблицу для решения задачи (В):
 Базисные
перемен. Базисные
перемен.
| Свободн.
члены
| x1
| x2
| x3
| x4
| x5
|
| x4
| 8
| 1
| 1(*)
| 1
| 1
| 0
|
| x5
| 5
| 1
|
| -1
| 0
| 1
|
| g(X)
| 13
| 2
|
| 0
| 0
| 0
|
| x2
|
|
|
|
|
|
|
| x5
| 5
| 1(*)
| 0
| -1
| 0
| 1
|
| g(X)
| 5
|
| 0
| -1
| -1
| 0
|
| x2
| 3
| 0
| 1
| 2
| 1
| -1
|
| x1
|
|
|
| -1
|
|
|
| g(X)
| 0
| 0
| 0
| 0
| -1
| -1
|
| x2
| 3
| 0
| 1
| 2
|
|
|
| x1
| 5
| 1
| 0
| -1
|
|
|
| f1(X)
| -18
| 0
| 0
| -1
|
|
|
В соответствии с постановкой задачи (В) заносим информацию об этой задаче в исходную симплекс – таблицу. В строке для целевой функции g(X)
два положительных элемента – 2 и 1, выбираем столбик, соответствующий элементу 1(он выделен полужирным шрифтом), в этом столбике над 1 только один положительный элемент – тоже 1 (в строке, соответствующей базисной переменной x4), а это означает, что переменная x4 исключается из числа базисных переменных, а на ее место приходит переменная x2 (она стоит над столбиком, выделенным полужирно). Преобразование таблицы начинается со старой строчки с x4, она без изменения переносится в новую часть таблицы, но уже с x2 в качестве базисной переменной («без изменения» потому, что ключевой элемент равен 1, а деление на 1 не меняет элементов). Строка новой части таблицы с базисной переменной x2 выделена жирно. Остальные элементы этой части таблицы преобразуются по «правилу двух перпендикуляров» на выделенные жирно строку и столбец. Далее, реализуется еще один шаг симплекс – метода, в результате которого переменная x5 уходит из числа базисных, а на ее место приходит переменная x1, а целевая функция g(X) достигает своего минимума, равного нулю. В соответствии с алгоритмом, заключительная часть таблицы переносится в новую часть, но уже с исходной целевой функцией f1(X), разумеется, эта функция пересчитывается на свободную переменную x3. В строке таблицы для f(X) нет положительных элементов (кроме c0 = 18), а это означает, что базисный план будет оптимальным, он получается из последней части таблицы: x1б = 5, x2б = 3, x3б =0, целевая функция исходной задачи на базисном плане также получается из таблицы: f(Xб) = 18.



 max
max b1
b1 0, x2
0, x2 
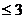 ,
,


 Базисные
перемен.
Базисные
перемен.



