

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...
Топ:
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В декартовых координатах вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
 Пусть область V ограничена снизу и сверху поверхностями z = z 1 (x, y) и z = z 2 (x, y) (z 1 (x, y) ≤ z 2 (x, y)). Тогда z 1 (x, y), z 2 (x, y) − определены и непрерывны на области D, которая является проекцией области V на плоскость Оху.
Пусть область V ограничена снизу и сверху поверхностями z = z 1 (x, y) и z = z 2 (x, y) (z 1 (x, y) ≤ z 2 (x, y)). Тогда z 1 (x, y), z 2 (x, y) − определены и непрерывны на области D, которая является проекцией области V на плоскость Оху.
Будем считать область V правильной в направлении оси Oz, т. е. любая прямая параллельная оси Oz, пересекает границу области не более чем в двух точках.
Тогда для любой функции f (x, y, z) непрерывной в области V, имеет место формула

позволяющая свести вычисление тройного интеграла к последовательному вычислению внутреннего определенного интеграла по переменной z (при постоянных х и у) и внешнего двойного интеграла по области D. Результат вычисления внутреннего интеграла есть функция двух переменных х и у.
Если область D ограничена линиями х = а и х = b (a < b), y = y 1(x) и y = y 2(x), где у 1 и у 2 − непрерывные на [ a, b ] функции, причем у 1 (х) ≤ у 2 (х), то переходя от двойного интеграла по области D к повторному, получаем формулу
 ,
,
 сводящую вычисление тройного интеграла к последовательному вычислению трех определенных интегралов. Порядок интегрирования может быть и другим. В частности, если V − параллелепипед с гранями х = а и х = b (a < b), y = с и y = d, z = ℓ и z = m (ℓ < m), то
сводящую вычисление тройного интеграла к последовательному вычислению трех определенных интегралов. Порядок интегрирования может быть и другим. В частности, если V − параллелепипед с гранями х = а и х = b (a < b), y = с и y = d, z = ℓ и z = m (ℓ < m), то
 .
.
В этом случае интегрирование можно проводить в любом порядке.
Пример 1. Вычислить  , где V − параллелепипед, образованный плоскостями х = − 1; х = 1; у = 0; у = 1; z = 0; z = 2.
, где V − параллелепипед, образованный плоскостями х = − 1; х = 1; у = 0; у = 1; z = 0; z = 2.
Решение. Подставим все известные значения в последнюю формулу и получим

Пример 2. Вычислить  , где V − параллелепипед, образованный плоскостями х + у + z = 1, х = 0; у = 0; z = 0.
, где V − параллелепипед, образованный плоскостями х + у + z = 1, х = 0; у = 0; z = 0.
|
|
Решение. Так как 0 ≤ z ≤ 1 − x − y, 0 ≤ y ≤ 1 − x, 0 ≤ x ≤ 1. Тогда

П. 19.2. Замена переменных в тройном интеграле.
Вычисление тройного интеграла в цилиндрических и
Сферических координатах.
Пусть требуется найти интеграл

Предположим, что тело А, находящееся в пространстве xyz, связано взаимно однозначно с телом В, находящимся в пространстве u uv, при помощи формул
x = x (u, u, v), y = y (u, u, v), z = z (u, u, v). (1)
Будем предполагать, что у функций x (u, u, v), y (u, u, v), z (u, u, v) существуют непрерывные частные производные по u, u, v. Тогда формула замены переменных в тройном интеграле запишется в виде
 , (2)
, (2)
где u, u, v − криволинейные координаты точки (x, y, z), J (u, u, v) − абсолютная величина якобиана
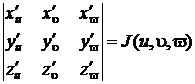
На практике часто встречаются два вида координат (x, y, z).
I. Цилиндрические координаты. Цилиндрическими координатами точки (x, y, z) называются числа r, j, z, где r и j − полярные координаты точки (x, y).
Ясно, что здесь
x = r cos j, y = r sin j, z = z
и потому якобиан этого преобразования

Стало быть, при переходе к цилиндрическим координатам общая формула (2) примет вид
 . (3)
. (3)
II. Сферические координаты. Сферическими координатам точки М (x, y, z) называются числа r, q, j, где q − угол между осью Оz и радиусом-вектором 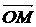 точки М, r − длина этого радиус-вектора, т. е. расстояние между началом координат О и точкой М, а j − двугранный угол между полуплоскостью с ребром Oz, содержащей положительную часть оси Ох, и точку М. Из рисунка видно, что
точки М, r − длина этого радиус-вектора, т. е. расстояние между началом координат О и точкой М, а j − двугранный угол между полуплоскостью с ребром Oz, содержащей положительную часть оси Ох, и точку М. Из рисунка видно, что
OP = r sin q.
Так как х и у − проекции  на оси Ох и Оу, а z − проекция
на оси Ох и Оу, а z − проекция 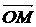 на ось Oz, то
на ось Oz, то
 . (4)
. (4)
Полезно отметить также очевидное соотношение r 2 = x 2 + y 2 + z 2.
Соответствие, даваемое формулами (4), не взаимно однозначно. Чтобы получить все пространство xyz, достаточно изменять точку (r, q, j) в области, определяемой неравенствами
0 ≤ r < + ¥, 0 ≤ q ≤ p, 0 ≤ j ≤ 2p,
|
|
но и при этом ограничении мы добиваемся взаимной однозначности, так как плоскости r = 0 пространства r qj в пространстве xyz отвечает одна точка (0, 0, 0), а точками (r, 0, 0) и (r, q,2p) отвечает одна и та же точка (r sinq, 0, r cosq). Связанные с этими нарушениями взаимной однозначности осложнения не мешают, однако, применимости к нашему случаю общей формулы (2). Мы примем это без доказательства.
Якобиан в этом случае будет равен

Тогда формула (2) примет вид
 .(5)
.(5)
Этой формулой удобно пользоваться тогда, когда f (x, y, z) имеет форму f (x 2 + y 2 + z 2), а также когда областью А служит шар x 2 + y 2 + z 2 ≤ R 2 или какая-нибудь простая часть такого шара и т. п.
Пример. Найти
 ,
,
если А − шар x 2 + y 2 + z 2 ≤ 1.
По формуле (5)
 .
.
Переходя к повторному интегралу, получаем
 .
.
Опуская простые пояснения, находим

Криволинейные интегралы.
Определение. 1. Пусть в декартовых координатах x, y, z в каждой точке M (x, y, z) кривой L задан вектор F, т. е. задана векторная функция F (M) точек M Î L, и определен единичный вектор  (М) касательной к этой кривой.
(М) касательной к этой кривой.
Разобьем кривую L на п частей; Δℓ i − длины отрезков разбиения (i = 1, 2, ¼, п). Внутри каждого отрезка разбиения произвольно возьмем точку Мi и вычислим в ней вектор F (Mi) и орт касательной  (Мi). Вычислим скалярное произведение F (Mi) ∙
(Мi). Вычислим скалярное произведение F (Mi) ∙  (Мi) и составим сумму
(Мi) и составим сумму
 (1)
(1)
которую назовем интегральной суммой векторной функции F (M) на кривой L.
Пусть l − длина наибольшего из элементов Δℓ i.
Если существует предел интегральной суммы (1) при n ® ¥ и l ® 0, то этот предел называется криволинейным интегралом и обозначается
 .
.
Таким образом,
 . (2)
. (2)
Определение 2. Так как скалярное произведение F (M) e (M) = f (M) − скалярная функция точек М кривой L, то равенство (2) может быть преобразовано в равенство
 , (3)
, (3)
левая часть которого называется криволинейным интегралом I − рода (или криволинейным интегралом по длине дуги кривой).
Определение 3. В декартовом базисе i, j, k, ассоциированном с принятой здесь системой декартовых координат, векторная функция F (M) и орт касательной e (M) задаются в виде

где P (M), Q (M), R (M) − скалярные функции точке М кривой L; a, b, g − углы, образуемые касательной к L в точках M Î L с осями координат x, y, z соответственно. Скалярное произведение этих векторов
|
|
F (M)∙ e (M) = P (M)∙cos a + Q (M)∙cos b + R (M)∙cos g. (4)
Пусть Δ x, Δ y, Δ z − проекции отрезка Δℓ на координатные оси. Тогда
Δ x = Δℓ∙cos a, Δ y = Δℓ∙cos b, Δ z = Δℓ∙cos g. (5)
Равенства (4), (5) позволяют записать
F (M)∙ e (M)∙Δℓ = P (M)∙Δ х + Q (M)∙Δ у + R (M)∙Δ z. (6)
С учетом этого равенство (2) преобразуется к виду
 . (7)
. (7)
Левая часть этого равенства называется криволинейным интегралом второго рода (или криволинейным интегралом по координатам).
Обратим внимание, что все три типа криволинейных интегралов (2), (3), (7) связаны друг с другом.
|
|
|

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!