

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
ВОПРОСЫ ПО МАТАНУ
| 1. | ФМП, область определения, линии уровня; частные производные, геометрический смысл. | |
| 2. | Дифференциал ФМП. Геометрический смысл. Свойства. | |
| 3. | Производная сложной функции. | |
| 4. | Производная по направлению. | |
| 5. | Касательная плоскость и нормаль к поверхности. | |
| 6. | Неявные функции F(x,y) = 0. Достаточные условия существования. Производная неявной функции. | |
| 7. | Формула Тейлора для функции 2-х переменных. | |
| 8. | Экстремум ФМП. Необходимые и достаточные условия существования. | |
| 9. | Критерий Сильвестра. | |
| 10. | Несобственный интеграл от непрерывной на бесконечном промежутке функции. Его свойства. | |
| 11. | Признак сравнения несобственного интеграла от неотрицательной функции. Следствие из признака сравнения. | |
| 12. | Несобственный интеграл от функций, неограниченных на отрезке. Признак сравнения. | |
| 13. | Двойной интеграл. Определение, условия существования, свойства. | |
| 14. | Теорема о среднем для двойного интеграла. | |
| 15. | Вычисление двойного интеграла. | |
| 16. | Двойной интеграл в полярных координатах. | |
| 17. | Геометрические и механические приложения двойного интеграла. | |
| 18. | Тройной интеграл. Условия существования. Свойства. | |
| 19. | Теорема о среднем для тройного интеграла. | |
| 20. | Вычисление тройного интеграла. Замена переменных в тройном интеграле. | |
| 21. | Цилиндрическая система координат. Тройной интеграл в цилиндрической системе координат. | |
| 22. | Сферическая система координат. Тройной интеграл в сферической системе координат. | |
| 23. | Геометрические и механические приложения тройного интеграла. | |
| 24. | Криволинейный интеграл первого рода. Определение, условия существования, свойства. | |
| 25. | Поверхностный интеграл первого рода. Определение, условия существования, свойства, вычисление. | |
| 26. | Знакопостоянные числовые ряды. Основные определения, свойства сходящихся рядов. | |
| 27. | Необходимые признаки сходимости числовых рядов. | |
| 28. | Достаточные признаки сходимости числовых рядов. | |
| 29. | Знакопеременные и знакочередующиеся числовые ряды. Абсолютная и условная сходимость. | |
| 30. | Признак Лейбница. | |
| 31. | Функциональные ряды. Определение. Область сходимости, равномерная сходимость. | |
| 32. | Критерий Коши и признак Вейерштрасса равномерной сходимости. | |
| 33. | Ряд Тейлора, его единственность. Основные разложения. | |
| 34. | Применение степенных рядов к приближенным вычислениям, к вычислению определенных интегралов. | |
| 35. | Криволинейный интеграл второго рода, определение, свойства. | |
| 36. | Связь криволинейного интеграла второго рода с криволинейным интегралом первого рода. | |
| 37. | Работа векторного поля, ее вычисление. | |
| 38. | Потенциальное векторное поле. Необходимые и достаточные условия потенциальности векторного поля. | |
| 39. | Поверхностный интеграл второго рода, определение, свойства. | |
| 40. | Вычисление поверхностного интеграла второго рода, связь с поверхностным интегралом первого рода. | |
| 41. | Символика Гамильтона. | |
| 42. | Дивергенция векторного поля. | |
| 43. | Формула Остроградского-Гаусса. | |
| 44. | Соленоидальные векторные поля. | |
| 45. | Ротор векторного поля. | |
| 46. | Свойства периодических функций. | |
| 47. | Ортогональность системы тригонометрических функций на отрезке  . .
| |
| 48. | Тригонометрический ряд Фурье для функций с периодом  . .
| |
| 49. | Формулировка условий разложимости функций в ряды Фурье. | |
| 50. | Ряды Фурье для четных и нечетных функций. | |
| 51. | Ряды Фурье для функций с периодом  .
Случай четных и нечетных функций. .
Случай четных и нечетных функций.
| |
| 52. | Ряды Фурье для функций, заданных на отрезке. Разложение в ряд по косинусу и синусу. | |
| 53. | Ряд Фурье в комплексной форме. | |
| 54. | Интеграл Фурье. Условия представимости функции интегралом Фурье. | |
| 55. | Интеграл Фурье для четных и нечетных функций. | |
| 56. | Интеграл Фурье в комплексной форме. |
|
|
|
|
1. ФМП, область определения, линии уровня; частные производные, геометрический смысл.



Производная по направлению.
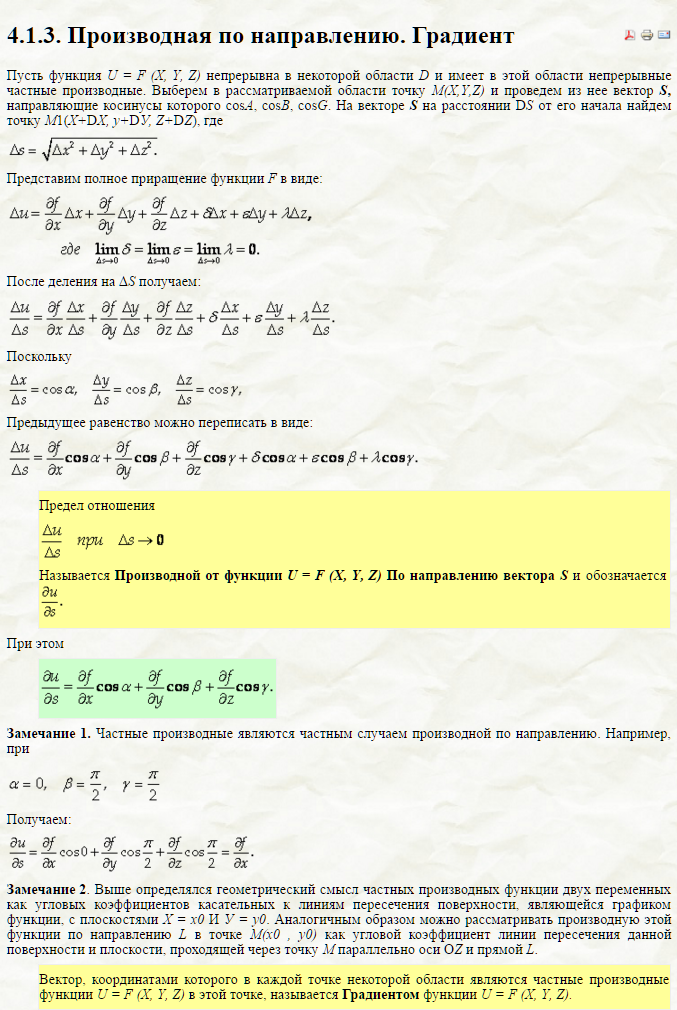
Критерий Сильвестра.

10-12. Несобственный интеграл…





13-17. Двойной интеграл…

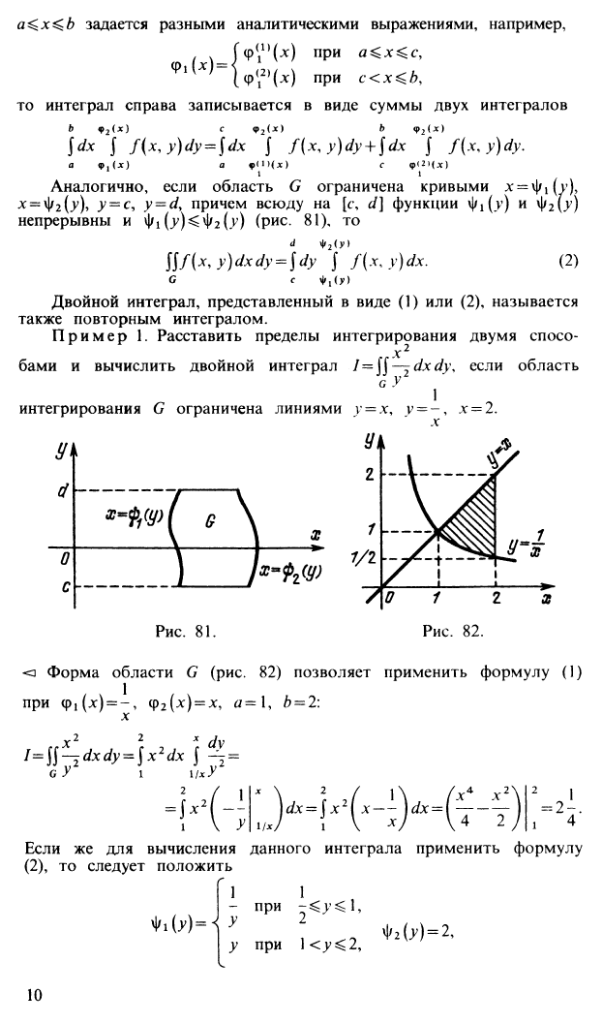









18-23. Тройной интеграл…






ИСТОЧНИКИ
· http://kvm.gubkin.ru/vip3p2/g4.pdf
· http://kvm.gubkin.ru/pub/avb/double_int.pdf
· http://matica.org.ua/metodichki-i-knigi-po-matematike
· http://eqworld.ipmnet.ru/ru/library/books/Kazimirov2002ru.pdf
ВОПРОСЫ ПО МАТАНУ
| 1. | ФМП, область определения, линии уровня; частные производные, геометрический смысл. | |
| 2. | Дифференциал ФМП. Геометрический смысл. Свойства. | |
| 3. | Производная сложной функции. | |
| 4. | Производная по направлению. | |
| 5. | Касательная плоскость и нормаль к поверхности. | |
| 6. | Неявные функции F(x,y) = 0. Достаточные условия существования. Производная неявной функции. | |
| 7. | Формула Тейлора для функции 2-х переменных. | |
| 8. | Экстремум ФМП. Необходимые и достаточные условия существования. | |
| 9. | Критерий Сильвестра. | |
| 10. | Несобственный интеграл от непрерывной на бесконечном промежутке функции. Его свойства. | |
| 11. | Признак сравнения несобственного интеграла от неотрицательной функции. Следствие из признака сравнения. | |
| 12. | Несобственный интеграл от функций, неограниченных на отрезке. Признак сравнения. | |
| 13. | Двойной интеграл. Определение, условия существования, свойства. | |
| 14. | Теорема о среднем для двойного интеграла. | |
| 15. | Вычисление двойного интеграла. | |
| 16. | Двойной интеграл в полярных координатах. | |
| 17. | Геометрические и механические приложения двойного интеграла. | |
| 18. | Тройной интеграл. Условия существования. Свойства. | |
| 19. | Теорема о среднем для тройного интеграла. | |
| 20. | Вычисление тройного интеграла. Замена переменных в тройном интеграле. | |
| 21. | Цилиндрическая система координат. Тройной интеграл в цилиндрической системе координат. | |
| 22. | Сферическая система координат. Тройной интеграл в сферической системе координат. | |
| 23. | Геометрические и механические приложения тройного интеграла. | |
| 24. | Криволинейный интеграл первого рода. Определение, условия существования, свойства. | |
| 25. | Поверхностный интеграл первого рода. Определение, условия существования, свойства, вычисление. | |
| 26. | Знакопостоянные числовые ряды. Основные определения, свойства сходящихся рядов. | |
| 27. | Необходимые признаки сходимости числовых рядов. | |
| 28. | Достаточные признаки сходимости числовых рядов. | |
| 29. | Знакопеременные и знакочередующиеся числовые ряды. Абсолютная и условная сходимость. | |
| 30. | Признак Лейбница. | |
| 31. | Функциональные ряды. Определение. Область сходимости, равномерная сходимость. | |
| 32. | Критерий Коши и признак Вейерштрасса равномерной сходимости. | |
| 33. | Ряд Тейлора, его единственность. Основные разложения. | |
| 34. | Применение степенных рядов к приближенным вычислениям, к вычислению определенных интегралов. | |
| 35. | Криволинейный интеграл второго рода, определение, свойства. | |
| 36. | Связь криволинейного интеграла второго рода с криволинейным интегралом первого рода. | |
| 37. | Работа векторного поля, ее вычисление. | |
| 38. | Потенциальное векторное поле. Необходимые и достаточные условия потенциальности векторного поля. | |
| 39. | Поверхностный интеграл второго рода, определение, свойства. | |
| 40. | Вычисление поверхностного интеграла второго рода, связь с поверхностным интегралом первого рода. | |
| 41. | Символика Гамильтона. | |
| 42. | Дивергенция векторного поля. | |
| 43. | Формула Остроградского-Гаусса. | |
| 44. | Соленоидальные векторные поля. | |
| 45. | Ротор векторного поля. | |
| 46. | Свойства периодических функций. | |
| 47. | Ортогональность системы тригонометрических функций на отрезке  . .
| |
| 48. | Тригонометрический ряд Фурье для функций с периодом  . .
| |
| 49. | Формулировка условий разложимости функций в ряды Фурье. | |
| 50. | Ряды Фурье для четных и нечетных функций. | |
| 51. | Ряды Фурье для функций с периодом  .
Случай четных и нечетных функций. .
Случай четных и нечетных функций.
| |
| 52. | Ряды Фурье для функций, заданных на отрезке. Разложение в ряд по косинусу и синусу. | |
| 53. | Ряд Фурье в комплексной форме. | |
| 54. | Интеграл Фурье. Условия представимости функции интегралом Фурье. | |
| 55. | Интеграл Фурье для четных и нечетных функций. | |
| 56. | Интеграл Фурье в комплексной форме. |
|
|
|
|
1. ФМП, область определения, линии уровня; частные производные, геометрический смысл.



Дифференциал ФМП. Геометрический смысл. Свойства.







|
|
|

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!