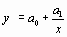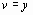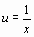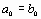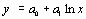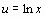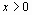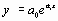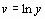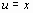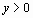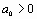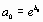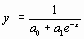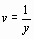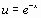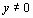Такая ситуация может возникнуть, например, в случае малых выборок. В качестве проверки гипотезы Но принимают СВ 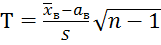 где S – "исправленное" среднее квадратическое отклонение. Случайная величина T имеет распределение Стьюдента ck=n-1степенями свободы. Критическая область, как и в рассмотренном выше случае с известной дисперсией D (X)=
где S – "исправленное" среднее квадратическое отклонение. Случайная величина T имеет распределение Стьюдента ck=n-1степенями свободы. Критическая область, как и в рассмотренном выше случае с известной дисперсией D (X)=  , строится в зависимости от вида конкурирующей
, строится в зависимости от вида конкурирующей
гипотезы.
Правило1. Для того, чтобы при заданном уровне значимости α проверить Гипотезу Но: α = 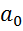 о равенстве неизвестной генеральной средней α нормальной совокупности с неизвестной дисперсией
о равенстве неизвестной генеральной средней α нормальной совокупности с неизвестной дисперсией  гипотетическому значению
гипотетическому значению 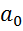 при конкурирующей гипотезе
при конкурирующей гипотезе 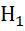 : α≠
: α≠ 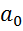 , необходимо вычислить
, необходимо вычислить
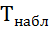 =
= 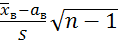 и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α, помещенному в верхней строке таблицы, и числу степеней свободы k=n-1 найти критическую точку
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α, помещенному в верхней строке таблицы, и числу степеней свободы k=n-1 найти критическую точку 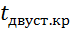 (α;k)двусторонней критической области. Если ǀ
(α;k)двусторонней критической области. Если ǀ 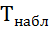 ǀ<
ǀ< 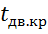 – нет оснований отвергнуть гипотезу Но; если ǀ
– нет оснований отвергнуть гипотезу Но; если ǀ 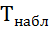 ǀ>
ǀ> 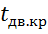 – гипотезу Но отвергают.
– гипотезу Но отвергают.
Правило2. При конкурирующей гипотезе 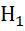 : α>
: α> 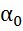 по заданному уровню значимости α, помещенному в нижней строке таблицы критических точек распределения Стьюдента, и числу степеней свободы k=n-1 найти критическую точку
по заданному уровню значимости α, помещенному в нижней строке таблицы критических точек распределения Стьюдента, и числу степеней свободы k=n-1 найти критическую точку 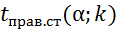 правосторонней критической области. Если –
правосторонней критической области. Если – 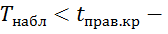 нет оснований отвергнуть гипотезу Но; если
нет оснований отвергнуть гипотезу Но; если  Гипотезу Но отвергают.
Гипотезу Но отвергают.
Правило3. При конкурирующей гипотезе 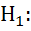 α<
α< 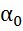 сначала по правилу 2 находят "вспомогательную" критическую точку
сначала по правилу 2 находят "вспомогательную" критическую точку 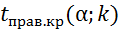 , а затем полагают границу левосторонней критической области
, а затем полагают границу левосторонней критической области 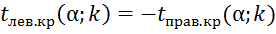 . Если
. Если 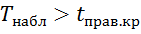 –нет оснований отвергнуть гипотезу Но; если
–нет оснований отвергнуть гипотезу Но; если 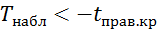 гипотезу Но отвергают.
гипотезу Но отвергают.
Для нахождения критической области необходимо знать критическое значение выборочной средней, которое можно найти из формулы для
статистики: 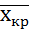 =
= 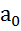 +
+ 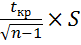
18.+ 19. Построение теоритического закона распределения по опытным данным. Метод наименьших квадратов для линейной зависимости и для квадратичной зависимости
Проверка гипотезы о предполагаемом законе распределения так же, как и проверка гипотезы о неизвестных параметрах известного закона распределения, производится при помощи специально подобранной случайной величины – критерия согласия. Как бы хорошо ни был подобран теоретический закон распределения, между эмпирическим и теоретическим распределениями неизбежны расхождения. Поэтому возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно. Для ответа на этот вопрос и служат критерии согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Одним из основных критериев согласия является критерий χ2 (критерий Пирсона).
Критерий Пирсона позволяет, в частности, проверить гипотезу о нормальном распределении генеральной совокупности. Для проверки этой гипотезы будем сравнивать эмпирические (т. е. наблюдаемые) и теоретические (т. е. вычисленные в предположении нормального закона распределения) частоты, которые, как правило, различаются.
Случайно (незначимо) или неслучайно (значимо) это расхождение? Ответ на этот вопрос и дает критерий согласия Пирсона. Для проверки предположения о нормальном распределении с помощью критерия Пирсона обычно выполняют следующий алгоритм.
1. Весь интервал наблюдаемых значений случайной величины X (выборки объема n) делят на k частичных интервалов ( 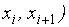 одинаковой длины, находят середины частичных интервалов
одинаковой длины, находят середины частичных интервалов
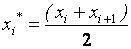 .
.
В качестве частоты ni варианты xi* принимают число вариант, попавших в i -й интервал. Получают последовательность равноотстоящих вариант и соответствующих им частот:
| xi*
| x 1 *
| x 2 *
| …
| x l *
|
|
| ni
| n 1
| n 2
| …
| n l
| 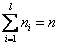
|
2. Вычисляют 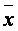 * и выборочное среднее квадратическое отклонение σ *.
* и выборочное среднее квадратическое отклонение σ *.
3. Нормируют случайную величину X, т. е. переходят к величине 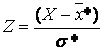 и вычисляют концы интервалов (
и вычисляют концы интервалов ( 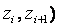 :
: 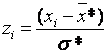 ,
, 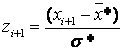 , причем полагают наименьшее значение z 1 = −∞, а наибольшее zк = +∞.
, причем полагают наименьшее значение z 1 = −∞, а наибольшее zк = +∞.
4. Вычисляют теоретические вероятности pi попадания случайной величины в интервалы ( 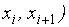 по формуле
по формуле
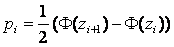 ,
,
где Φ(x) – функция Лапласа.
Находят теоретические частотыni' = npi.
Пусть по выборке объема нормально распределенной генеральной совокупности получено эмпирическое распределение
| xi
| x 1
| x 2
| …
| x l
|
|
| ni
| n 1
| n 2
| …
| n l
| 
|
и вычислены теоретические частоты ni ’.
Необходимо при уровне значимости α проверить справедливость нулевой гипотезы H 0: {генеральная совокупность распределена нормально}.
В качестве критерия проверки гипотезы H 0 примем случайную величину
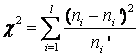 . (2.18)
. (2.18)
Величина, определенная формулой (2.18), – это случайная величина, так как в различных опытах она принимает различные, неизвестные заранее значения. Ясно, что χ2 → 0 при ni → ni', т. е. чем меньше различаются эмпирические ni и теоретические ni' частоты, тем меньше значение критерия χ2. Таким образом, критерий характеризует близость эмпирического и теоретического распределения.
Известно, что при n → ∞ закон распределения случайной величины χ2 стремится к закону распределения χ2 с k степенями свободы. Поэтому случайная величина в формуле (2.18) обозначается через χ2, а сам критерий называют критерием согласия χ2.
Число степеней свободы k находят из равенства k = l – r – 1, где l число групп (частичных интервалов); r – число параметров предполагаемого распределения, которые оценены по данным выборки (для нормального закона распределения r = 2, поэтому k = l – 3).
Построим правостороннюю критическую область (так как односторонний критерий более «жестко» отвергает гипотезу H 0), исходя из требования, чтобы в предположении справедливости гипотезы H0, вероятность попадания критерия в эту область была равна принятому уровню значимости α: 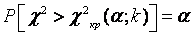 . Следовательно, правосторонняя критическая область определяется неравенством
. Следовательно, правосторонняя критическая область определяется неравенством  , а область принятия гипотезы H 0– неравенством
, а область принятия гипотезы H 0– неравенством 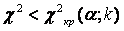 .
.
Значение критерия, вычисленное по данным наблюдений, обозначим χ2набл. Сформулируем правило проверки нулевой гипотезы H 0. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H0: {генеральная совокупность распределена нормально}, необходимо вычислить теоретические частоты ni' и наблюдаемое значение критерия согласия χ2 Пирсона 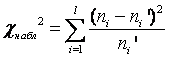 . По таблице критических точек распределения χ2 по заданному уровню значимости α и числу степеней свободы
. По таблице критических точек распределения χ2 по заданному уровню значимости α и числу степеней свободы
k = l – 3найти критическую точку 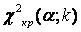 .
.
Если наблюдаемое значение критерия χ2набл попало в область принятия гипотезы 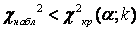 , то нет оснований отвергнуть нулевую гипотезу H 0 (рис. 2.6).
, то нет оснований отвергнуть нулевую гипотезу H 0 (рис. 2.6).
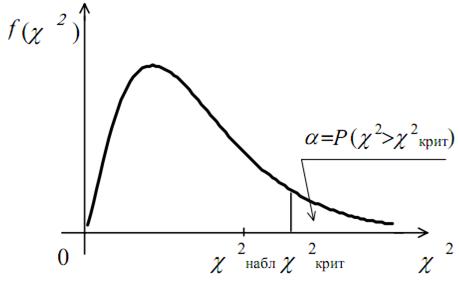
Рис. 2.6. Иллюстрация принятия нулевой гипотезы с помощью критерия Пирсона
Если наблюдаемое значение критерия χ2 набл попало в критическую область 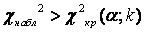 , то нулевую гипотезу H 0 отвергают (рис. 2.7).
, то нулевую гипотезу H 0 отвергают (рис. 2.7).
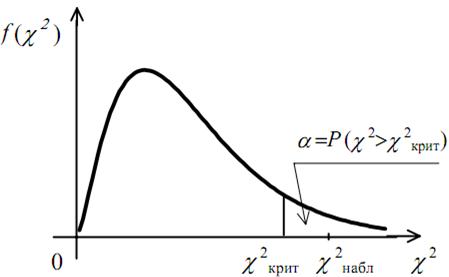
Рис. 2.7. Иллюстрация случая, когда отвергают нулевую гипотезу с помощью критерия Пирсона
Для контроля вычислений наблюдаемого критерия χ 2набл можно использовать равенство
 .
.
Критерий Стьюдента был разработан английским химиком У. Госсетом. Публикации своих статей по t -критерию У. Госсет сделал в 1908 г. в журнале «Биометрика» под псевдонимом «Student», что в переводе означает «Студент». В отечественной же литературе принято писать «Стьюдент». Коварная простота вычисления t -критерия Стьюдента, а также его наличие в большинстве статистических пакетов и программ привели к широкому использованию этого критерия даже в тех условиях, когда применять его нельзя.
Наиболее часто t -критерий используется в двух случаях. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная и опытная группы, состоящие, например, из разных пациентов, количество которых в группах может быть различно. Во втором же случае используется так называемый парный t -критерий, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних. Поэтому эти выборки называют зависимыми, связанными. Например, измеряется содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения. В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп.
Критерий Стьюдента является наиболее часто используемым методом обнаружения различия между средними двух выборок. Например, t- критерий можно использовать для сравнения средних показателей группы пациентов, принимавших определенное лекарство, с контрольной группой, где принималось безвредное лекарство. Теоретически t -критерий может применяться даже если размеры выборок очень небольшие (например, 10; некоторые исследователи утверждают, что можно исследовать выборки меньшего размера), и если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны.
Предположение о нормальности можно проверить, исследуя распределение (например, визуально с помощью гистограммы) или применяя какой-либо критерий нормальности.
Чтобы применить t -критерий для независимых выборок, требуется, по крайней мере, одна независимая (группирующая) переменная (например, Пол: мужчина/женщина) и одна зависимая переменная (например, тестовое значение некоторого показателя, кровяное давление, число лейкоцитов и т. д.). С помощью специальных значений независимой переменной (эти значения называются кодами, например, мужчина и женщина) данные разбиваются на две группы.
На практике часто приходится сравнивать более двух групп данных (например, имеется лекарство 1, лекарство 2 и успокоительное лекарство) или сравнивать группы, созданные более чем одной независимой переменной (например, Пол, тип Лекарства и Доза). В таких более сложных исследованиях необходимо использовать дисперсионный анализ, который можно рассматривать как обобщение t- критерия.
Степень различия между средними в двух группах зависит от внутригрупповой вариации (дисперсии) переменных. В зависимости от того, насколько различны эти значения для каждой группы, «грубая разность» между групповыми средними показывает более сильную или более слабую степень зависимости между независимой (группирующей) и зависимой переменными. Например, если среднее значение числа лейкоцитов (WCC) равнялось 102 для мужчин и 104 для женщин, то разность внутригрупповых средних только на величину 2 будет чрезвычайно важной, когда все значения WCC мужчин лежат в интервале от 101 до 103, а все значения WCC женщин – в интервале 103–105. В этом случае можно довольно хорошо предсказать WCC (значение зависимой переменной) исходя из пола субъекта (независимой переменной). Однако если та же разность 2 получена из сильно разбросанных данных (например, изменяющихся в пределах от 0 до 200), то этой разностью вполне можно пренебречь. Таким образом, можно сказать, что уменьшение внутригрупповой вариации увеличивает чувствительность критерия.
Критерий Стьюдента зависимых выборок очень полезен в тех довольно часто возникающих на практике ситуациях, когда важный источниквнутригрупповой вариации (или ошибки) может быть легко определен и исключен из анализа. Например, это относится к экспериментам, в которых две сравниваемые группы основываются на одной и той же совокупности наблюдений (субъектов), которые тестировались дважды (например, до и после лечения, до и после приема лекарства). В подобных экспериментах значительная часть внутригрупповой изменчивости (вариации) в обеих группах может быть объяснена индивидуальными различиями субъектов.
Заметим, что на самом деле, такая ситуация не слишком отличается от той, когда сравниваемые группы совершенно независимы, где индивидуальные отличия также вносят вклад в дисперсию ошибки. Однако в случае независимых выборок, вы ничего не сможете поделать с этим, так как не сможете определить (или «удалить») часть вариации, связанную с индивидуальными различиями субъектов. Если та же самая выборка тестируется дважды, то можно легко исключить эту часть вариации. Вместо исследования каждой группы отдельно и анализа исходных значений, можно рассматривать просто разности между двумя измерениями (например, «до приема лекарства» и «после приема лекарства») для каждого субъекта. Вычитая первые значения из вторых (для каждого субъекта) и анализируя затем только эти «чистые (парные) разности», можно исключить ту часть вариации, которая является результатом различия в исходных уровнях индивидуумов. Именно так и проводятся вычисления в
t- критерии для зависимых выборок. В сравнении с t- критерием для независимых выборок, такой подход дает всегда «лучший» результат (критерий становится более чувствительным).
Метод наименьших квадратов
Пусть на вход некоторого устройства подается сигнал  , а на выходе измеряется сигнал
, а на выходе измеряется сигнал 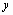 . Известно, что величины
. Известно, что величины  и
и 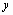 связаны функциональной зависимостью, но какой именно – неизвестно. Требуется приближенно определить эту функциональную зависимость
связаны функциональной зависимостью, но какой именно – неизвестно. Требуется приближенно определить эту функциональную зависимость 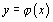 по опытным данными. Пусть в результате
по опытным данными. Пусть в результате 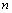 измерений получен ряд экспериментальных точек
измерений получен ряд экспериментальных точек 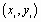 . Известно, что через
. Известно, что через 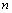 точек можно всегда провести кривую, аналитически выражаемую многочленом
точек можно всегда провести кривую, аналитически выражаемую многочленом 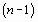 -й степени. Этот многочлен называют интерполяционным. И вообще, замену функции
-й степени. Этот многочлен называют интерполяционным. И вообще, замену функции 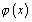 на функцию
на функцию 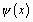 так, что их значения совпадают в заданных точках
так, что их значения совпадают в заданных точках
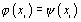 ,
, 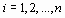 , (1.1)
, (1.1)
называют интерполяцией.
Однако такое решение проблемы не является удовлетворительным, поскольку 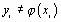 из-за случайных ошибок измерения и влияния на измерения значений
из-за случайных ошибок измерения и влияния на измерения значений 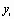 помех и шумов в устройстве. Так что
помех и шумов в устройстве. Так что
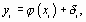 (1.2)
(1.2)
где 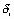 – некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьшихквадратов. Сглаживающую кривую называют аппроксимирующей.
– некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьшихквадратов. Сглаживающую кривую называют аппроксимирующей.
Задача аппроксимации решается следующим образом. В декартовой прямоугольной системе координат наносят точки 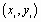 . По расположению этих точек высказывается предположение о принадлежности искомой функции к определенному классу функций. Например, линейная функция
. По расположению этих точек высказывается предположение о принадлежности искомой функции к определенному классу функций. Например, линейная функция  , квадратичная
, квадратичная 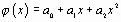 и т.д. В общем случае
и т.д. В общем случае  . Неизвестные параметры функции
. Неизвестные параметры функции 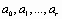 определяются из требования минимума суммы квадратов случайных ошибок, т.е. минимума величины
определяются из требования минимума суммы квадратов случайных ошибок, т.е. минимума величины
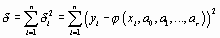 . (1.3)
. (1.3)
Величина 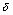 называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки:
называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки:
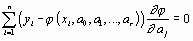 ,
, 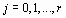 . (1.4)
. (1.4)
Решая систему уравнений, находим неизвестные параметры 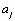 и тем самым полностью определяем функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует (приближает) искомую функцию
и тем самым полностью определяем функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует (приближает) искомую функцию 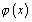 .
.
Остановимся подробнее на линейной зависимости  .
.
Дифференцируя, получим следующую систему уравнений
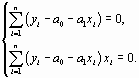 (1.5)
(1.5)
Из первого уравнения находим 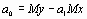 , где
, где
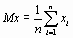 ,
, 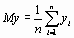 . (1.6)
. (1.6)
Подставляя выражение для 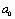 во второе уравнение, найдем
во второе уравнение, найдем
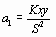 , (1.7)
, (1.7)
где
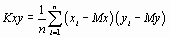 ,
, 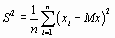 . (1.8)
. (1.8)
Таким образом,
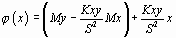 (1.9)
(1.9)
есть искомая линейная функция.
Ввиду простоты расчетов аппроксимация линейной зависимости используется довольно часто. Кроме того, многие функции, зависящие от двух параметров, можно линеаризовать путем замены переменных.
Для этого необходимо подобрать такое преобразование исходной зависимости 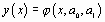 , в результате которого она приобретает линейный вид
, в результате которого она приобретает линейный вид 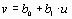 . Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты
. Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты 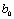 и
и 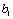 пересчитываются в коэффициенты
пересчитываются в коэффициенты 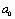 и
и 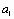 .
.
Для ряда часто встречающихся двухпараметрических зависимостей возможные замены переменных (а также, обратные замены для пересчета 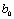 и
и 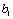 в
в 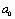 и
и 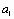 ) приведены в табл. 1.1.
) приведены в табл. 1.1.
| Вид зависимости
| Замена переменных
| Ограничения
| Обратная замена переменных
|
Гиперболическая 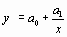
| 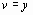
| 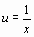
| 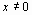
| 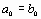
| 
|
Логарифмическая 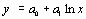
| 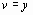
| 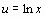
| 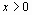
| 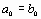
| 
|
Показательная 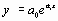
| 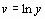
| 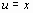
| 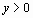
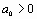
| 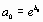
| 
|
Степенная 
| 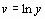
| 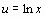
| 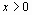 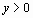 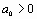
| 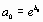
| 
|
Комбинированная 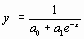
| 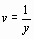
| 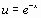
| 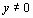
| 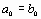
| 
|



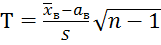 где S – "исправленное" среднее квадратическое отклонение. Случайная величина T имеет распределение Стьюдента ck=n-1степенями свободы. Критическая область, как и в рассмотренном выше случае с известной дисперсией D (X)=
где S – "исправленное" среднее квадратическое отклонение. Случайная величина T имеет распределение Стьюдента ck=n-1степенями свободы. Критическая область, как и в рассмотренном выше случае с известной дисперсией D (X)=  , строится в зависимости от вида конкурирующей
, строится в зависимости от вида конкурирующей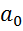 о равенстве неизвестной генеральной средней α нормальной совокупности с неизвестной дисперсией
о равенстве неизвестной генеральной средней α нормальной совокупности с неизвестной дисперсией 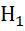 : α≠
: α≠ 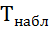 =
= 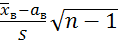 и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α, помещенному в верхней строке таблицы, и числу степеней свободы k=n-1 найти критическую точку
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α, помещенному в верхней строке таблицы, и числу степеней свободы k=n-1 найти критическую точку 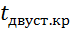 (α;k)двусторонней критической области. Если ǀ
(α;k)двусторонней критической области. Если ǀ 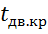 – нет оснований отвергнуть гипотезу Но; если ǀ
– нет оснований отвергнуть гипотезу Но; если ǀ 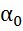 по заданному уровню значимости α, помещенному в нижней строке таблицы критических точек распределения Стьюдента, и числу степеней свободы k=n-1 найти критическую точку
по заданному уровню значимости α, помещенному в нижней строке таблицы критических точек распределения Стьюдента, и числу степеней свободы k=n-1 найти критическую точку 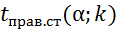 правосторонней критической области. Если –
правосторонней критической области. Если – 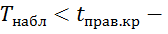 нет оснований отвергнуть гипотезу Но; если
нет оснований отвергнуть гипотезу Но; если  Гипотезу Но отвергают.
Гипотезу Но отвергают.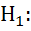 α<
α< 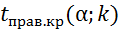 , а затем полагают границу левосторонней критической области
, а затем полагают границу левосторонней критической области 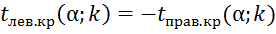 . Если
. Если 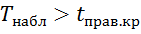 –нет оснований отвергнуть гипотезу Но; если
–нет оснований отвергнуть гипотезу Но; если 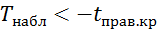 гипотезу Но отвергают.
гипотезу Но отвергают.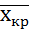 =
= 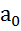 +
+ 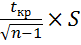
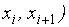 одинаковой длины, находят середины частичных интервалов
одинаковой длины, находят середины частичных интервалов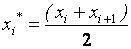 .
.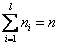
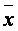 * и выборочное среднее квадратическое отклонение σ *.
* и выборочное среднее квадратическое отклонение σ *.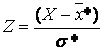 и вычисляют концы интервалов (
и вычисляют концы интервалов ( 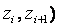 :
: 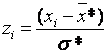 ,
, 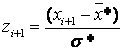 , причем полагают наименьшее значение z 1 = −∞, а наибольшее zк = +∞.
, причем полагают наименьшее значение z 1 = −∞, а наибольшее zк = +∞.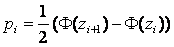 ,
,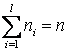
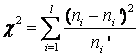 . (2.18)
. (2.18)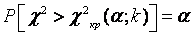 . Следовательно, правосторонняя критическая область определяется неравенством
. Следовательно, правосторонняя критическая область определяется неравенством  , а область принятия гипотезы H 0– неравенством
, а область принятия гипотезы H 0– неравенством 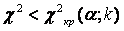 .
.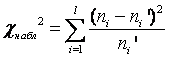 . По таблице критических точек распределения χ2 по заданному уровню значимости α и числу степеней свободы
. По таблице критических точек распределения χ2 по заданному уровню значимости α и числу степеней свободы 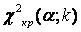 .
.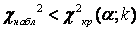 , то нет оснований отвергнуть нулевую гипотезу H 0 (рис. 2.6).
, то нет оснований отвергнуть нулевую гипотезу H 0 (рис. 2.6).
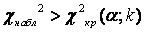 , то нулевую гипотезу H 0 отвергают (рис. 2.7).
, то нулевую гипотезу H 0 отвергают (рис. 2.7).
 .
. , а на выходе измеряется сигнал
, а на выходе измеряется сигнал 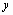 . Известно, что величины
. Известно, что величины 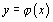 по опытным данными. Пусть в результате
по опытным данными. Пусть в результате 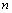 измерений получен ряд экспериментальных точек
измерений получен ряд экспериментальных точек 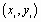 . Известно, что через
. Известно, что через 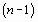 -й степени. Этот многочлен называют интерполяционным. И вообще, замену функции
-й степени. Этот многочлен называют интерполяционным. И вообще, замену функции 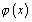 на функцию
на функцию 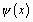 так, что их значения совпадают в заданных точках
так, что их значения совпадают в заданных точках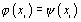 ,
, 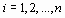 , (1.1)
, (1.1)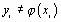 из-за случайных ошибок измерения и влияния на измерения значений
из-за случайных ошибок измерения и влияния на измерения значений 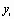 помех и шумов в устройстве. Так что
помех и шумов в устройстве. Так что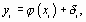 (1.2)
(1.2)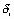 – некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьшихквадратов. Сглаживающую кривую называют аппроксимирующей.
– некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьшихквадратов. Сглаживающую кривую называют аппроксимирующей. , квадратичная
, квадратичная 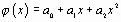 и т.д. В общем случае
и т.д. В общем случае  . Неизвестные параметры функции
. Неизвестные параметры функции 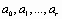 определяются из требования минимума суммы квадратов случайных ошибок, т.е. минимума величины
определяются из требования минимума суммы квадратов случайных ошибок, т.е. минимума величины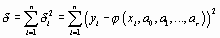 . (1.3)
. (1.3)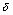 называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки:
называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки: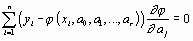 ,
, 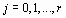 . (1.4)
. (1.4)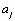 и тем самым полностью определяем функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует (приближает) искомую функцию
и тем самым полностью определяем функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует (приближает) искомую функцию 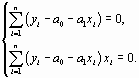 (1.5)
(1.5)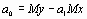 , где
, где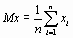 ,
, 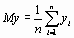 . (1.6)
. (1.6)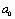 во второе уравнение, найдем
во второе уравнение, найдем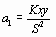 , (1.7)
, (1.7)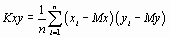 ,
, 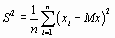 . (1.8)
. (1.8)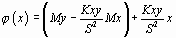 (1.9)
(1.9)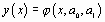 , в результате которого она приобретает линейный вид
, в результате которого она приобретает линейный вид 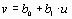 . Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты
. Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты 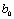 и
и 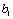 пересчитываются в коэффициенты
пересчитываются в коэффициенты 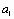 .
.