Если  ,
,  , то
, то
 ;
;
 ;
;
 .
.
Длина вектора:  .
.
Координаты вектора, если известны координаты
его начала  и конца
и конца  :
:
 ,
,
длина вектора:  .
.
Координаты точки  , принадлежащей отрезку
, принадлежащей отрезку  , и делящей его в отношении
, и делящей его в отношении 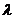 (
( ):
):
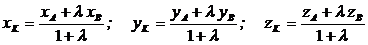 .
.
Если точка  середина отрезка
середина отрезка  , то
, то
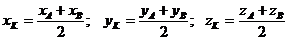 .
.
Скалярное произведение векторов и его свойства
Определение скалярного произведения
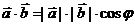 , где
, где  - угол между векторами
- угол между векторами  и
и 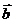
(если 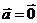 или
или 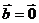 , то
, то 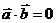 ).
).
Свойства: 1) 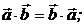 2)
2) 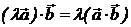 (
(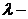 число);
число);
3) 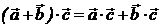 .
.
Выражение скалярного произведения векторов через координаты векторов:
если  ,
,  , то
, то 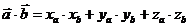 .
.
Выражение скалярного произведения через проекции:
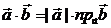 или
или 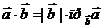 .
.
Косинус угла между векторами  и
и 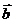 вычисляется по формуле:
вычисляется по формуле:
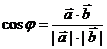 ,
,
или через координаты векторов:

Правые и левые тройки векторов. Тройку некомпланарных ненулевых векторов 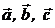 , взятых в указанном порядке, называют правой тройкой, если после приведения их к одному началу при взгляде из конца третьего вектора на плоскость первых двух векторов кратчайший поворот от первого вектора ко второму кажется совершающимся против часовой стрелки. Если – по часовой стрелке, то тройку называют левой.
, взятых в указанном порядке, называют правой тройкой, если после приведения их к одному началу при взгляде из конца третьего вектора на плоскость первых двух векторов кратчайший поворот от первого вектора ко второму кажется совершающимся против часовой стрелки. Если – по часовой стрелке, то тройку называют левой.
Векторное произведение векторов и его свойства
Определение векторного произведения
Векторным произведением двух ненулевых неколлинеарных векторов  и
и 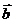 называется такой вектор
называется такой вектор 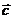 , который обозначается
, который обозначается 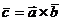 , и обладает следующими свойствами:
, и обладает следующими свойствами:
1) 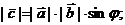 где
где  - угол между векторами
- угол между векторами  и
и 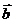 ;
;
2) 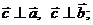
3) векторы 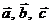 в указанном порядке образуют правую тройку.
в указанном порядке образуют правую тройку.
Если один из векторов  или
или 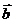 нулевой, или векторы
нулевой, или векторы  и
и 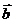 коллинеарны, то
коллинеарны, то 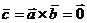 .
.
Свойства: 1) 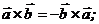 2)
2)  (
(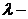 число);
число);
3) 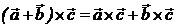 .
.
Если векторы  и
и 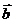 заданы своими координатами, т.е.
заданы своими координатами, т.е. 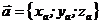 ,
, 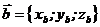 , то векторное произведение находится по формуле
, то векторное произведение находится по формуле 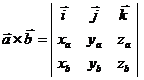 , или в координатной форме
, или в координатной форме 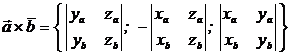 .
.
Длина вектора 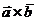 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах  и
и 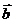 как на сторонах, если эти векторы приведены к одному началу:
как на сторонах, если эти векторы приведены к одному началу: 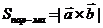 .
.
Смешанное произведение векторов
Определение. Смешанным произведением трех векторов 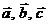 называют скалярное произведение векторов
называют скалярное произведение векторов 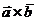 и
и 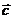 . Обозначают смешанное произведение
. Обозначают смешанное произведение 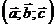 . Итак,
. Итак, 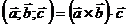 .
.
Если известны координаты векторов 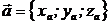 ,
, 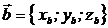 ,
, 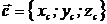 , то смешанное произведение находится по формуле
, то смешанное произведение находится по формуле
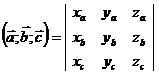 .
.
Объем параллелепипеда, построенного на векторах 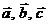 как на сторонах, если эти векторы приведены к одному началу, находится по формуле:
как на сторонах, если эти векторы приведены к одному началу, находится по формуле: 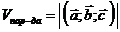 .
.
Объем пирамиды, построенной на векторах 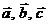 как на сторонах, если эти векторы приведены к одному началу, находится по формуле:
как на сторонах, если эти векторы приведены к одному началу, находится по формуле:
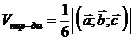 .
.
Если  , то тройка векторов
, то тройка векторов 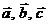 - правая, если же
- правая, если же 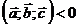 , то тройка
, то тройка 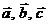 - левая.
- левая.
Условие коллинеарности двух векторов
В векторной форме:  .
.
В координатной форме: если  ,
,  , то
, то
 .
.
Условие перпендикулярности двух векторов
В векторной форме: 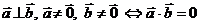 .
.
В координатной форме: если 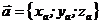 ,
, 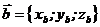 , то
, то
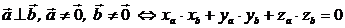 .
.
Условие компланарности трех векторов
В векторной форме:
ненулевые векторы 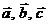 компланарны в том и только том случае, если
компланарны в том и только том случае, если 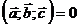 .
.
В координатной форме: если 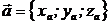 ,
, 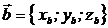 ,
, 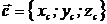 , то ненулевые векторы
, то ненулевые векторы 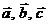 компланарны в том и только том случае, если
компланарны в том и только том случае, если 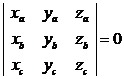 .
.
Прямая на плоскости



 ,
,  , то
, то ;
; ;
; .
. .
. и конца
и конца  :
: ,
, .
. , принадлежащей отрезку
, принадлежащей отрезку  , и делящей его в отношении
, и делящей его в отношении 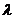 (
( ):
):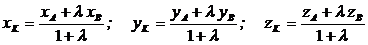 .
.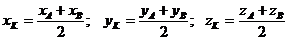 .
.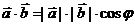 , где
, где  - угол между векторами
- угол между векторами  и
и 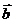
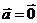 или
или 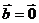 , то
, то 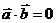 ).
).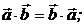 2)
2) 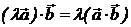 (
(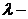 число);
число);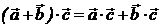 .
. ,
,  , то
, то 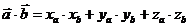 .
.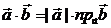 или
или 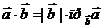 .
.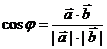 ,
,
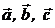 , взятых в указанном порядке, называют правой тройкой, если после приведения их к одному началу при взгляде из конца третьего вектора на плоскость первых двух векторов кратчайший поворот от первого вектора ко второму кажется совершающимся против часовой стрелки. Если – по часовой стрелке, то тройку называют левой.
, взятых в указанном порядке, называют правой тройкой, если после приведения их к одному началу при взгляде из конца третьего вектора на плоскость первых двух векторов кратчайший поворот от первого вектора ко второму кажется совершающимся против часовой стрелки. Если – по часовой стрелке, то тройку называют левой.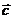 , который обозначается
, который обозначается 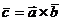 , и обладает следующими свойствами:
, и обладает следующими свойствами: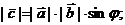 где
где  - угол между векторами
- угол между векторами 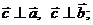
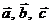 в указанном порядке образуют правую тройку.
в указанном порядке образуют правую тройку.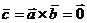 .
.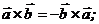 2)
2)  (
(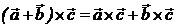 .
.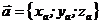 ,
, 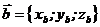 , то векторное произведение находится по формуле
, то векторное произведение находится по формуле 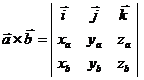 , или в координатной форме
, или в координатной форме 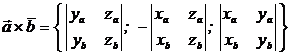 .
.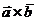 численно равна площади параллелограмма, построенного на векторах
численно равна площади параллелограмма, построенного на векторах 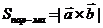 .
.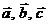 называют скалярное произведение векторов
называют скалярное произведение векторов 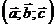 . Итак,
. Итак, 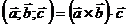 .
.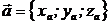 ,
, 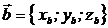 ,
, 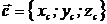 , то смешанное произведение находится по формуле
, то смешанное произведение находится по формуле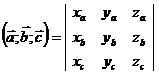 .
.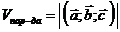 .
.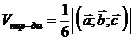 .
. , то тройка векторов
, то тройка векторов 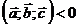 , то тройка
, то тройка  .
. .
.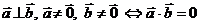 .
.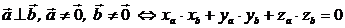 .
.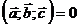 .
.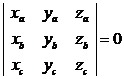 .
.


