Тема 2. Числовые последовательности
Если каждому числу n из натурального ряда чисел 1, 2, 3, …, n поставлено в соответствие действительное число xn, то множество действительных чисел x1, x2, …, xn называется числовой последовательностью.
x1, x2, …, xn - элементы последовательности
n – номер последовательности
обозначение: сокращенно: { xn }
Арифметические действия над числовыми последовательностями
1. Произведение на постоянное число m
m { xn }={ m x xn }={ mx1, mx2, mx3 … mxn}
2. Сумма { xn }+{ yn }={ xn + yn }={ x1 + y1, x2 + y2, xn + yn}
3. Разность { xn }-{ yn }={ xn - yn }={ x1 - y1, x2 - y2,… xn - yn}
4. Частное

При условии, что yn ¹0
Убывающая последовательность – это такая последовательность, у которой каждый предыдущий член больше последующего, т.е.
an+1 < an для всех n
| {
|
| }
| a1 = 1,
| a2 =
|
| , a3 =
|
| Если an+1 - an < 0, то убывающая
|
| n
|
|
| Если an+1 - an > 0, то возрастающая
|
Возрастающая последовательность – это такая последовательность, у которой каждый последующий член последовательности больше предыдущего, т.е.
an< an+1 для всех n
| 1.
| {
|
| }
|
т.к.
|
|
<
|
|
- убывающая
| |
| n2
| (n +1)2
| n2
| |
| 2.
| {
| 3 n -1
| }
| an=
| 3n-1
| an+1 =
| 3 n+ 2
| |
| n
| n
| n +1
| |
| | 3n+2
| –
| 3 n -1
| =
| 3 n 2+2 n -(3 n -1)(n +1)
| =
|
|
>0
|
| | n +1
| n
| n (n +1)
| n (n +1)
|
| | | | | | | | | | | | | | | | | | | | | | | |
т.е. an+1 > an - возрастающая
Предел числовой последовательности
Число a называется пределом числовой последовательности, если существует такое положительное число e, для которого выполняется условие:
ï xn - a ï<e, при этом последовательность { xn } называется сходящейся.
Обозначение: lim xn = a
Или: Число a называется пределом числовой последовательности, если
при n ® ¥ xn® a
Если последовательность не имеет предела, она называется расходящейся.
Свойства сходящихся последовательностей
1. Если все элементы бесконечно малой последовательности { an }= одному и тому же числу c, то c = 0.
2. Сходящаяся последовательность имеет только один предел
3. Предел от суммы двух последовательностей равен сумме пределов этих последовательностей.
lim (an± bn) = lim an± lim bn
n® ¥ n® ¥ n® ¥
4. Предел произведения двух последовательностей равен произведениям этих последовательностей
lim an x bn= lim an x lim bn
n® ¥ n® ¥ n® ¥
5. Предел частности двух последовательностей равен частному от пределов двух последовательностей
|
lim
n® ¥
|
an
|
=
| lim an
n® ¥
|
| bn
| lim bn
n® ¥
|
6. Предел произведения постоянной величины с на последовательность аn равен произведению постоянной величины на предел этой последовательности
lim (с an) = c x lim an
n® ¥ n® ¥
7. Предел постоянной величины равен самой этой величине.
lim c = c
n® ¥
Пример:
| lim
n® ¥
| 8 n - 3
|
=
| lim
n® ¥
| 8 n
| -
|
| =
| lim
n® ¥
| 8 -
|
| =
| lim
n® ¥
| 8 -
| lim
n® ¥
|
| =
| 8 - 0
| = -
|
|
| n
| n
| n
| n
|
| 13 -7 n
|
| -
| 7 n
|
| - 7
| lim
n® ¥
|
| -
| lim
n® ¥
|
| 0 - 7
|
|
| n
| n
| n
| n
|
| | | | | | | | | | | | | | | | | | | | | | |
Тема 3.
Функции
Величина y называется функцией переменной величины x, если каждому значению x, соответствует одно или несколько определенных значений y.
При этом переменная x называется аргументом
Величина y зависит от величины x
Обозначение: y =¦(x) пример S=πR2
L=υt
Способы задания функций:
1. Табличный способ – функциональная зависимость записывается таблицей
2. Графический способ – состоит в изображении графика функции, т.е. множества точек (x, y) на плоскости
3. Аналитический способ состоит в задании функции одной или несколькими формулами:
a) Явный способ y = x2
b) Неявный способ xy = 5 Þ 
c) Параметрический способ x = cos t; y = sin t
Основные свойства функций
1. Четность и нечетность
Функция y = ¦(x) называется четной, если для любых значений x из области определения, ¦(-x) =¦(x) и нечетной, если ¦(-x) = – ¦(x)
Четная функция симметрична относительно оси OY.
Пример: (-x) 2= x2 – функция четная; (-х) 3= –х3 – функция нечетная.
Четная функция симметрична относительно оси OY.
Нечетная функция симметрична относительно начала координат.
2. Монотонность.
Функция ¦=¦(x) называется возрастающей на промежутке x, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция ¦=¦(x) называется убывающей на промежутке x, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
3. Ограниченность.
Функция ¦(x) называется ограниченной с двух сторон на промежутке x, если существует такое положительное число M>0, для которого всегда выполняется условие:
ç ¦(x) ç £ M для любого x принадлежащего множеству x
Пример y = sin x
Ограничена на всей числовой оси, ç sin x ç £ 1
¦(x) £ M - ограниченная сверху
Пример: у = - х2 + 2
¦(x) ≥ m – ограниченная снизу
Пример: у = х2 + 3
4. Периодичность.
Функция ¦(x) называется периодической с периодом Т ¹ 0, если для любых x из области определения функции выполняется условие: ¦ (x + Т ) =¦(x)
Пример: y = sin x имеет период Т = 2p (выполняется условие периодичности)
Предел функции.
Число b называется пределом функции ¦(x), при x ® a,если по мере того как x приближается a, значение ¦(x) неограниченно приближается к b.
lim ¦(x) = b
 x ® a
x ® a
n = 1, 2, 3
Ноль (0) – предел последовательности
Непрерывность функции.
Определение 1: функция ¦(x) называется непрерывной в (·) x0, если предел этой функции и ее значение в этой точке равны, т.е.

Определение 2: функция y = ¦(x) называется непрерывной, если выполняется условие lim Dy = 0
Dx ® 0
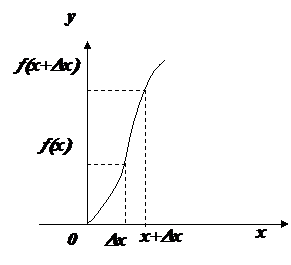 D (дельта) – разность между новым и старым значением или D - приращение
D (дельта) – разность между новым и старым значением или D - приращение
D y = ¦ (x+Dx) - ¦(x) -приращение функции
Dx = (x+Dx) - x приращение аргумента D x


 Определение 3: предел слева: lim ¦(x)
Определение 3: предел слева: lim ¦(x)
x ® x0 – 0

 предел справа: lim ¦(x)
предел справа: lim ¦(x)

x ® x0 + 0
Функция называется непрерывной в (·) x0, если предел “слева” совпадает с пределом “справа” и равен значению функции в (·) x0.

Функция ¦(x) называется разрывной в ( · ) x0, если в этой точке не выполнено не одно из трех условий непрерывности (определение 1, 2, 3).
Замечательные пределы.

Асимптота.
Асимптотой называется прямая, к которой приближается точка графика функции при неограниченном удалении ее от начала координат.
Существует три вида асимптот:
1. вертикальная
2. горизонтальная
3. наклонная
Правила нахождения асимптот:
1. Вертикальная асимптота бывает в точках, где функция не существует (х ≠ х0). Если хотя бы один из пределов функции: слева или справа, не существует, то прямая х = х0 является вертикальной асимптотой.
2. Пусть функция определена при достаточно больших Х и существует конечный предел
является горизонтальной асимптотой
3. Пусть функция определена при достаточно больших
Х и существует конечный предел
и
тогда прямая y = kx + b является наклонной асимптотой
Тема 4. Производная.
Производной функции y = ¦(x) в точке x0 называется предел при D x ® 0 отношения приращения функции в этой точке к приращению аргумента (при условии, что этот предел существует)
| y¢ = lim
D x ® 0
| D y
| = lim
D x ® 0
| ¦ (x0 + Dx) -¦(x0)
|
| D x
| D x
|
Производная функции имеет несколько обозначений
| y¢; ¦ ¢(x);
| dy
| ;
| d ¦(x)
|
| dx
| dx
|
Нахождение производной функции называется дифференцированием этой функции.
Геометрический смысл производной.

Пусть функция y = ¦(x) определена и непрерывна на [a, b]
Пусть (·) M соответствует некоторому значению x0, а (·) P значению x0 +D x, где D x - приращение аргумента
Проведем через (·)M и (·)P прямую (секущую).
Ðj (D x) - угол между секущей и осью 0 x.
Касательной S к графику функции ¦(x) в (·)M называется предельное положение секущей MP при неограниченном приближении (·)P по графику к (·)M (или то же самое при D x ® 0)
| tg j(Dx)=
| NP
| =
| Dy
| =
| ¦ (x0+Dx) - ¦ (x0)
|
| MN
| Dx
| Dx
|
Т.к. при Dx ® 0 секущая MP переходит в касательную, то Ðj0 – угол касательной с осью 0x.
lim tg j(Dx) = tg j0
D x ® 0
С другой стороны
| lim tg j(Dx) = lim
D x ® 0 D x ® 0
| ¦ (x0+ Dx) - ¦(x0)
| = ¦¢(x0) Þ ¦¢(x0) = tg j0
|
| Dx
|
Производная функции ¦¢(x) в (·)x0 равна угловому коэффициенту касательной к графику функции ¦(x) в точке M (x0, ¦(x0)).
Уравнение касательной y = ¦(x0) -¦¢(x0)(x- x0)
Физический смысл производной: скорость изменения функции в точке.
Функция ¦(x) называется дифференцируемой в (·)x0, если её приращение Dy в этой точке можно представить в виде: Dy = A * Dx + a(Dx)* Dx
A - некоторое число, не зависящее от Dx,
a(Dx) – функция аргумента Dx, являющаяся бесконечно малой при Dx ® 0,
т.е. lim a(Dx) = 0
D x ® 0
Значение производной функции  в точке
в точке  обозначают
обозначают  .
.
Дифференциалом dx независимой переменной х называют её приращение  .
.
Дифференциалом  называется
называется  .
.
Примечание: производная функции  есть некоторая функция
есть некоторая функция  , произведенная (т.е. полученная по определенным правилам) из данной функции.
, произведенная (т.е. полученная по определенным правилам) из данной функции.
Правила дифференцирования
Пусть ¦(x) = U y(x) = V
1. C¢ = 0, где C = const
2. [a ´ ¦(x)]¢ = a ´ ¦¢(x) – (постоянная a выносится за знак дифференциала)
[a ´ U]¢ = a ´ U¢
3. (U + V)¢ = U¢ + V¢ – (производная суммы равна сумме производных)
4. (U ´ V)¢ = U¢V + UV¢
5. (UVW)¢ = U¢VW + UV¢W + UVW¢
| 6.
| (
| U
| )¢
| =
| U¢V - UV¢
|
| V
| V2
|
7. Производная степенной функции: y=xn y¢ = n ´ xn-1
8. Производная тригонометрических функций:
а) y = sin x y¢ = cos x
б) y = cos x y¢ = - sin x
в) y = tg x
г) y = ctg x
9. Производная логарифмической функции y = loga x
10. Производная показательной функции y = ax
y¢ = ax ln a
y = ex Þ y¢ = ex
11. Производная сложной функции
Если y = ¦ (g(x)), то y¢(x)¢ = ¦¢(g) ´ g¢(x) или y = ¦(U), где U = g(x) Þ
y¢ = ¦¢(U) ´ U¢
Пример нахождения производной:
y = ln(x3 + 1)
заменим (x3 + 1) новой переменной z, тогда y = ln z
Производная
y¢ = (lnz)¢ z¢
(lnz)¢ =
z¢ = (x
3 + 1)¢ = = (x
3)¢ + (1)¢ = 3x
3-1 + 0 = 3x
2
y¢ =
Правило Лопиталя раскрытия неопределенностей.
Пусть функции f(x) и  дифференцируемы в окрестности точки а, причем производная
дифференцируемы в окрестности точки а, причем производная  .
.
Если обе функции бесконечно малые или бесконечно большие при 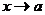 , т.е. если частное
, т.е. если частное 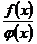 в точке а представляет неопределенность вида
в точке а представляет неопределенность вида  или
или  , то
, то  , при условии, что предел отношения производных существует (конечный или бесконечный).
, при условии, что предел отношения производных существует (конечный или бесконечный).
Правило применимо и для случая, когда  . Раскрытие неопределенностей вида
. Раскрытие неопределенностей вида  ,
,  ,
,  ,
,  ,
,  при помощи алгебраических преобразований и логарифмирования сводится к раскрытию неопределенностей вида
при помощи алгебраических преобразований и логарифмирования сводится к раскрытию неопределенностей вида  и
и  .
.
Замечание: правило Лопиталя применимо тогда, когда существует предел отношения производных. Если предел отношения функций существует, а предел отношения производных не существует, надо раскрывать неопределенности другим способом.
Производную  от у = f(x) будем называть производной первого порядка; производную от первой производной называют второй производной (или производной второго порядка) от функции у = f(x) и обозначают
от у = f(x) будем называть производной первого порядка; производную от первой производной называют второй производной (или производной второго порядка) от функции у = f(x) и обозначают  или
или  ; производную от производной второго порядка называют третьей производной и обозначают
; производную от производной второго порядка называют третьей производной и обозначают  или
или  и т.д.
и т.д.
Производная от производной (n – 1)-го порядка называется производной n-го порядка от функции у = f(x) и обозначается  или
или  .
.
Если функция у = f(x) дифференцируема в интервале (a,b) и имеет положительную (отрицательную) производную  , то функция f(x) возрастает (убывает) в этом интервале.
, то функция f(x) возрастает (убывает) в этом интервале.
Замечание: производная в отдельных точках интервала может равняться нулю.
тема 2. Числовые последовательности
Если каждому числу n из натурального ряда чисел 1, 2, 3, …, n поставлено в соответствие действительное число xn, то множество действительных чисел x1, x2, …, xn называется числовой последовательностью.
x1, x2, …, xn - элементы последовательности
n – номер последовательности
обозначение: сокращенно: { xn }





 x ® a
x ® a
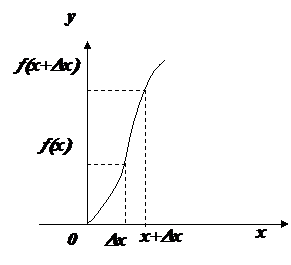 D (дельта) – разность между новым и старым значением или D - приращение
D (дельта) – разность между новым и старым значением или D - приращение

 Определение 3: предел слева: lim ¦(x)
Определение 3: предел слева: lim ¦(x)
 предел справа: lim ¦(x)
предел справа: lim ¦(x)


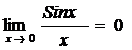




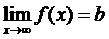



 в точке
в точке  обозначают
обозначают  .
. .
. называется
называется  .
. , произведенная (т.е. полученная по определенным правилам) из данной функции.
, произведенная (т.е. полученная по определенным правилам) из данной функции.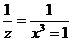

 дифференцируемы в окрестности точки а, причем производная
дифференцируемы в окрестности точки а, причем производная  .
.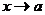 , т.е. если частное
, т.е. если частное 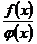 в точке а представляет неопределенность вида
в точке а представляет неопределенность вида  или
или  , то
, то  , при условии, что предел отношения производных существует (конечный или бесконечный).
, при условии, что предел отношения производных существует (конечный или бесконечный). . Раскрытие неопределенностей вида
. Раскрытие неопределенностей вида  ,
,  ,
,  ,
,  ,
, 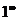 при помощи алгебраических преобразований и логарифмирования сводится к раскрытию неопределенностей вида
при помощи алгебраических преобразований и логарифмирования сводится к раскрытию неопределенностей вида  от у = f(x) будем называть производной первого порядка; производную от первой производной называют второй производной (или производной второго порядка) от функции у = f(x) и обозначают
от у = f(x) будем называть производной первого порядка; производную от первой производной называют второй производной (или производной второго порядка) от функции у = f(x) и обозначают  или
или  ; производную от производной второго порядка называют третьей производной и обозначают
; производную от производной второго порядка называют третьей производной и обозначают  или
или  и т.д.
и т.д. или
или  .
.


