

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Геометрический смысл предела функции  на бесконечности заключается в том, что для любого
на бесконечности заключается в том, что для любого  найдется такое число
найдется такое число 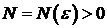 , что для всех
, что для всех 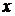 , которые принадлежат объединению интервалов:
, которые принадлежат объединению интервалов:  , соответствующие значения функции
, соответствующие значения функции  попадают в
попадают в  – окрестность числа
– окрестность числа 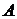 , т.е. точки графика функции
, т.е. точки графика функции  при соответствующих значениях
при соответствующих значениях 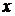 лежат в полосе шириной
лежат в полосе шириной  , ограниченной горизонтальными прямыми
, ограниченной горизонтальными прямыми 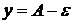 и
и  .
.
5.4. Односторонние пределы
Определение 5.5. Число  называется левосторонним пределом функции
называется левосторонним пределом функции  при
при 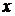 , стремящимся к
, стремящимся к  , если для любого положительного числа
, если для любого положительного числа  , как бы мало оно ни было, найдется такое положительное число
, как бы мало оно ни было, найдется такое положительное число  , что для всех
, что для всех 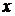 , удовлетворяющих неравенству:
, удовлетворяющих неравенству:  , будет справедливо неравенство
, будет справедливо неравенство 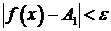 . Обозначается:
. Обозначается:  .
.
Определение 5.6. Число  называется правосторонним пределом функции
называется правосторонним пределом функции  при
при 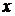 , стремящимся к
, стремящимся к  , если для любого положительного числа
, если для любого положительного числа  , как бы мало оно ни было, найдется такое положительное число
, как бы мало оно ни было, найдется такое положительное число  , что для всех
, что для всех 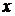 , удовлетворяющих неравенству:
, удовлетворяющих неравенству:  , будет справедливо неравенство
, будет справедливо неравенство  . Обозначается:
. Обозначается:  .
.
Определение 5.7. Число  называется пределом функции
называется пределом функции  при
при 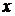 стремящимся к
стремящимся к  слева, если функции
слева, если функции  определена на промежутке
определена на промежутке  , и какова бы ни была последовательность
, и какова бы ни была последовательность  , сходящаяся к точке
, сходящаяся к точке  слева, т.е.такая, что
слева, т.е.такая, что 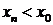 для всех натуральных
для всех натуральных  , соответствующая ей последовательность значений функции
, соответствующая ей последовательность значений функции 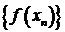 существует и сходится к числу
существует и сходится к числу  . Это записывают, как:
. Это записывают, как:  или
или  .
.
Определение 5.8. Число  называется пределом функции
называется пределом функции  при
при 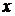 стремящимся к
стремящимся к  справа, если функции
справа, если функции  определена на промежутке
определена на промежутке 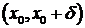 , и какова бы ни была последовательность
, и какова бы ни была последовательность  , сходящаяся к точке
, сходящаяся к точке  справа, т.е.такая, что
справа, т.е.такая, что  для всех натуральных
для всех натуральных  , соответствующая ей последовательность значений функции
, соответствующая ей последовательность значений функции 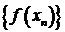 существует и сходится к числу
существует и сходится к числу  . Это записывают, как:
. Это записывают, как:  или
или  .
.
Если  определена в интервале
определена в интервале  , то в точке
, то в точке 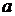 может иметь смысл только число
может иметь смысл только число  , а в точке
, а в точке  – только число
– только число  .
.
|
|
Отметим, что двусторонний предел  существует лишь тогда, когда существуют оба односторонних предела, которые равны друг другу, то есть
существует лишь тогда, когда существуют оба односторонних предела, которые равны друг другу, то есть  .
.
В этом случае 
Бесконечно большие функции
Определение 5.9. Функция  называется бесконечно большой в точке
называется бесконечно большой в точке  , если для любой последовательности значений аргумента
, если для любой последовательности значений аргумента  соответствующая последовательность значений функции
соответствующая последовательность значений функции  является бесконечно большой.
является бесконечно большой.
Определение 5.10. Функция  называется бесконечно большой в точке
называется бесконечно большой в точке  , если для любого положительного числа
, если для любого положительного числа 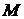 , как бы велико оно ни было, существует такое число
, как бы велико оно ни было, существует такое число  , что для всех
, что для всех 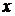 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , справедливо неравенство
, справедливо неравенство  .
.
То, что функция  является бесконечно большой в точке
является бесконечно большой в точке  , соответствует тому, что
, соответствует тому, что 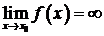 . Кратко это записывают так:
. Кратко это записывают так:  .
.
5.8. С войства функций, имеющих пределы
Теорема 5.2. Если существует конечный предел 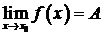 , то для всех
, то для всех 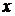 принадлежащих некоторой окрестности точки
принадлежащих некоторой окрестности точки  функция
функция  является ограниченной, т.е. существуют такие положительные числа
является ограниченной, т.е. существуют такие положительные числа 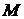 и
и  , что для всех
, что для всех 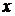 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , следует, что
, следует, что  .
.
Доказательство. Из условия теоремы следует, что для любого  найдется такое число
найдется такое число  , что для всех
, что для всех 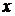 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , следует
, следует  . Возьмем
. Возьмем  . И раскроем последнее неравенство по свойству модуля:
. И раскроем последнее неравенство по свойству модуля:  .
.
Или  . Отсюда следует, что
. Отсюда следует, что  . Если взять
. Если взять  , то получим, что
, то получим, что 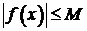 , что и требовалось. Теорема доказана.
, что и требовалось. Теорема доказана.
Теорема 5.3. Если существует конечный предел 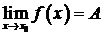 , и
, и 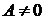 , то для всех
, то для всех 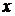 принадлежащих некоторой окрестности точки
принадлежащих некоторой окрестности точки  функция
функция  удовлетворяет условию:
удовлетворяет условию:  . Более того, для указанных
. Более того, для указанных 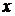 функция
функция 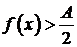 , если
, если  , и
, и  , если
, если  .
.
Доказательство. Из условия теоремы следует, что для любого  (в частности, возьмем
(в частности, возьмем  ) найдется такое число
) найдется такое число  , что для всех
, что для всех 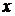 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , следует
, следует  . Раскроем последнее неравенство:
. Раскроем последнее неравенство:  , которое выполняется для всех
, которое выполняется для всех 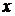 окрестности точки
окрестности точки  . Получили
. Получили  . Или
. Или  для указанных
для указанных 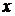 . При
. При  следует, что
следует, что  и
и 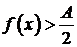 . При
. При  следует, что
следует, что  для всех
для всех 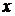 окрестности точки
окрестности точки  . Тогда, раскрывая модуль в неравенстве
. Тогда, раскрывая модуль в неравенстве  , получаем
, получаем  или
или  , что и требовалось доказать.
, что и требовалось доказать.
|
|
Теорема 5.4. Еслисуществуют конечные пределы 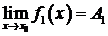 и
и  , и для всех
, и для всех 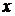 принадлежащих некоторой окрестности точки
принадлежащих некоторой окрестности точки  функции
функции  и
и  удовлетворяют неравенству
удовлетворяют неравенству  , то
, то  .
.
Доказательство. Пусть последовательность  сходится к
сходится к  . Тогда для существует достаточно большой номер
. Тогда для существует достаточно большой номер  , что при всех
, что при всех  следует:
следует:
 , а после предельного перехода в последнем неравенстве, получаем:
, а после предельного перехода в последнем неравенстве, получаем:  , что и требовалось.
, что и требовалось.
|
|
|

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!