Методы анализа и синтеза всех классов дискретных автоматов состоят на базе алгебры логики. Основным понятием алгебры логики является понятие высказывания. Под высказыванием понимается любое утверждение, которое оценивается только с точки зрения его истинности или ложности. Другие качественные характеристики высказывания (хорошее, плохое, едкое, литературное, политическое и т.д.) не рассматриваются. Высказывания может быть либо истинным, либо ложным. Считается, что истинно-ложных и ложно-истинных высказываний не существует. Исчисление высказываний основано на том, что каждое высказывание можно рассматривать как некоторую двоичную переменную. В соответствии с двоичной природой высказывания и условились называть их логическими (булевыми) переменными и обозначать буквами латинского алфавита, приписывая им значение 1- в случае истинности и значение 0 – в случае ложности. В качестве примера приведем два высказывания:
х = “Советские люди первыми шагнут в космос”.
у = “Волга – крупнейшая река Азии”.
Первое из них истинно, второе не соответствует действительности и является ложным. Следовательно можно записать: х = 1, у = 0.
Высказывания могут быть простым или сложным. Высказывания называется простым, если его значение истинности не зависит от значений истинности каких-либо других высказываний. Такое высказывание содержит одну простую законченную мысль. Приведенное в качестве примера высказывания Х и Y являются простыми.
Сложным называется высказывание, значение истинности которого зависит от значений истинности других высказываний.
Следовательно, любое сложное высказывание можно считать логической
(булевой) функцией некоторых двоичных аргументов – простых высказываний, входящих в его состав.
Функцию f (х1, х2, …хn) называют функцией алгебры логики (ФАЛ), если она, как и ее аргументы может принимать только два значения: 0 и 1. Переменные ФАЛ сопоставляют со значением сигналов на входах дискретного автомата, а значение функции алгебры логики – со значением сигналов на его выходах.
Реальные дискретные автоматы имеют конечное число входов, следовательно, число переменных у соответствующих ФАЛ тоже конечно.
Так как переменные ФАЛ могут принимать только два значения, область определения ФАЛ конечна.
Способы задания ФАЛ
Существует ряд способов задания ФАЛ.
1. При словесном описании логической функции должны быть перечислены совокупности единичных и нулевых наборов или указаны их характерные свойства. Набором называют совокупное значение переменных. Каждому набору переменных соответствует определенное значение функции. Наборы переменных, на которых логическая функция принимает значение 1, называют единичными наборами, а наборы, на которых функция принимает значение 0, называют, нулевыми наборами.
Пример словесного описания функции:
функция трех переменных задана единичными и нулевыми наборами. Единичные наборы содержат две или более переменных, равных единице (т.е. это наборы 011, 110, 101, 111), а все остальные наборы (000, 001, 010,100) – являются нулевыми.
2. При табличном наборе ФАЛ задают таблицей ее значений в зависимости от значений переменных. Например, в табл.2 задана ФАЛ трех переменных: f (х1, х2, х3).
Таблица 2.
Каждому набору переменных соответствует определенное значение функции.При трех переменных можно образовать восемь наборов. Следовательно, приведенная в табл.2 функция определена на 8 наборах. Каждый набор представляет собой трехразрядное двоичное число. Если ФАЛ содержит п переменных, двоичные числа будут п-разрядные, и→, общее число наборов будет N = 2п.
Таблицу, в которой для всех наборов переменных приводятся значения ФАЛ, наз. таблицей истинности. При п переменных таблица содержит 2п строк (по числу наборов), п столбцов (по числу переменных) и один столбец значений функции. Крайний левый столбец (номер набора) является десятичным эквивалентом двоичного набора переменных.
3. При графическом способе наборами значений переменных ФАЛ сопоставляются точки п-мерного пространства. Множество 2п наборов определяет множество вершин п-мерного единичного куба. Вершинам куба соответствуют наборы значений переменных и приписаны значения функции на этих наборах, т.е. областью определения ФАЛ, зависящей от п-переменных, является множество вершин единичного п-мерного куба.
 х2 Функция f (x1,x2,x3),заданная
х2 Функция f (x1,x2,x3),заданная

 таблицей истинности (табл. 2)
таблицей истинности (табл. 2)

 010 0 0 может быть задана графически.
010 0 0 может быть задана графически.


 110 0 111 1
110 0 111 1

 001
001

 000 0 1 х3
000 0 1 х3


 100 0 0 101
100 0 0 101
х1
Рис. 4 Графический способ задания ФАЛ.
4. При координатном способе функцию задают в виде координатной карты состояния, которую называют Карта Карно. Карты представляют собой прямоугольные таблицы, разделенные горизонтальными и вертикальными линиями на клетки. Общее число клеток соответствует числу наборов функции. Все переменные функции разбивают на 2 группы. Одна группа переменных определяет выбор строки, другая – столбца. На пересечении строки и столбца находится клетка, в которую записывают значение функции при соответствующем наборе переменных. Разделение переменных на группы осуществляется так, чтобы в соседних клетках наборы различались только значением одной переменной.
 x2x3
x2x3



 x1 00 01 11 10
x1 00 01 11 10
 0 1 1
0 1 1
1 1
Рис.5 Функция f(x1,x2x3) заданная табл. истинности (табл. 2),представлена картой Карно.
5.При числовым способе каждому набору переменных ставят в соответствие определенное число в двоичной системе и присваивают десятичный номер, равный эквиваленту двоичного числа. Функцию задают в виде десятичных номеров тех наборов переменных, на которых она принимает значение 1.
Функция f (х1, х2, х3), приведенная в табл.2, может быть задана числовым способом так: f = {1, 3, 7} х1 х2 х3. Обратить особое внимание на порядок следования переменных.
6.При
аналитическом (алгебраическом) способе функцию задают в виде алгебраического выражения, показывающего, какие и в какой последовательности должны выполнятся логические операции над аргументами. Алгебраические выражения может быть составлено из наборов аргументов, на которых функция принимает значение 1, или из наборов аргументов, на которых она принимает значение 0. Аналитическое выражение для функции f (х
1, х
2, х
3), заданной табл.2, имеет вид:
Операции алгебры логики
Техническая интерпретация логических выражений может быть насмотрена как аналогия между высказываниями и электрическими переключателями, поскольку и те и другие имеют двоичную природу.
Любое истинное высказывание изображается в виде замкнутого, а любое ложное высказывание- в виде разомкнутого контакта. На основе принятой аналогии любую логическую функцию можно изобразить в виде некоторой переключательной схемы (вот почему логические функции часто называют переключательными). Рассмотрим переключатель, показанный на рис.6
 x x
| f
|
|
|
|
|
|
|
Рис.6. а) – простейшая переключательная контактная схема
б) – таблица истинности f = х
Этот переключатель связывает между собой две точки: Р и Q. Состояние переключателя может быть выражено с помощью булевой переменной Х, которая может принимать два значения 0 и 1. Если переключатель разомкнут, то Х = 0, а если замкнут то Х = 1. Состояние соединения РQ может быть выражено с помощью булевой функции f, которая принимает одно из двух значений: 0 или 1. Если связи между точками Р и Q нет, то f = 0, если есть - f = 1. Эти результаты сведены в таблицу истинности (Рис. 6б), из которой ясно, что f = х.
2. Операция И (логическое умножение, конъюнкция)
Два переключателя А и В соединены последовательно и связывают точки Р и Q (Рис.7). Пусть состояния переключателей выражаются с помощью двух булевых переменных х1 и х2. Если переключатель А разомкнут, то х1 = 0, если разомкнут, то х1 = 1. Аналогично, х2 = 0 или х2 = 1, в зависимости от того, разомкнут или замкнут переключатель В. Состояние соединения РQ выражается с помощью булевой функции f, значение которой зависит от наличия связи между точками Р и Q (рис 7.а)
 P Q
P Q


 б)
б)

 x1 & f
x1 & f
 x2
x2
в)
Рис. 7. а)- переключательная контактная схема, реализующая операцию И;
б)- таблица истинности функции И.
в)- условное обозначение элемента И.
Существует четыре возможные комбинации значений переменных х1 и х2. .
Они сведены в таблицу истинности (рис 7б). Функцию И называют функцией булевого (логического) умножения, конъюнкцией и записывают в виде: f = х1 * х2 или f = х1 ^ х2. В цифровых системах функция “И” реализуется с помощью электронной схемы, называемой элементом И. Условное обозначение элемента И на функциональных схемах изображено на Рис.7в. Функция И истинна, если истинны все ее аргументы. Исходя из этого определения, можно вывести такие свойства функции И:
1) результат многократного логического умножения аргумента самого на себя равен исходному аргументу: х * х * х….х = х;
2) логическое произведение двух аргументов из которых первый заведомо является истинным, равно второму аргументу: 1 * х = х
3) логическое произведение двух аргументов, из которых один заведомо является ложным, равно нулю: 0 * х = 0;
4)
логическое произведение некоторого аргумента х и его отрицания х равно нулю:
3.Операция НЕ (логическое отрицание, инверсия)
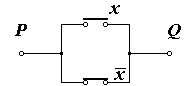
Рассмотрим переключательную схему на Рис.8а. Она состоит из двух связанных переключателей: если один из них замкнут, то другой обязательно разомкнут. На Рис.8а разомкнутый переключатель представляется булевой переменной Х, замкнутый – булевой переменной Х. Для верхнего переключателя Х = 0, когда этот переключатель разомкнут, а для нижнего переключателя, который замкнут, когда верхний разомкнут, Х = 1. Говорят, что Х есть инверсия Х или НЕ Х. Следовательно, черта над булевой переменной Х означает инверсию (или отрицание) переменной.
 х х
| x
| f
|
|
|
|
|
|
|
|
|
а) б)
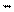
Рис.8 а) – переключательная схема функции f = х + х
 б) - таблица истинности f = х + х
б) - таблица истинности f = х + х
Связь между точками Р и Q существует всегда т.к. f = 1 в любом случае, независимо, верхний или нижний переключатель замкнут: т.е. х + х = 1. Уравнение двойственное по отношению к любому булевому уравнению, получается заменой нужного знака “ + “ не “ * “ и заменой всех 1 на 0 и наоборот. По отношению к вышеприведенному уравнению эта процедура приводит к х * х = 0


 x x
| x
| f
|
|
|
|
|
|
|
|
|
а) б)
 Рис.9 а) – переключательная схема функции f = х * х
Рис.9 а) – переключательная схема функции f = х * х
 б) – таблица истинности f = х * х
б) – таблица истинности f = х * х
Инвертор может быть реализован с помощью электронной схемы, условное обозначение которой приведена на рис.9.
 х х
| f=x
|
|
|
|
|
|
|



 1
1



Условное обозначение инвертора и его табл. истинности.
Функция НЕ истинна, если ложен её аргумент, и наоборот.
Эта функция обладает следующими свойствами:
1)двойное отрицание (а также любое четное количество отрицаний) некоторого аргумента х равно самому аргументу: х=х;
2)тройное отрицание (а также любое нечетное количество отрицаний) некоторого аргумента х равно отрицанию этого аргумента х=х;
3)если имеется некоторое логическое равенство, то отрицание обеих его частей не нарушает этого равенства, т.е. если f1 = f2, то и f1 = f2.
1.Операция ИЛИ (логическое сложение, дизъюнкция.)
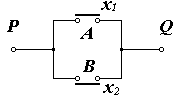 На рис. 10 два переключателя А и В соединены параллельно и связывают точки Р и Q. Состояния переключателей и соединения Р Q выпрямляются с помощью булевых переменных х1, х2 и f соответственно. Если оба переключателя А и В разомкнуты, то х1=0, х2=0 и ясно, что связи между точками Р Q нет;→ f=0. С другой стороны, если переключатель А замкнут, а В разомкнут, то х1=1, х2=0 и связь между точками Р иQ осуществляется с помощью переключателя А,→f=1.
На рис. 10 два переключателя А и В соединены параллельно и связывают точки Р и Q. Состояния переключателей и соединения Р Q выпрямляются с помощью булевых переменных х1, х2 и f соответственно. Если оба переключателя А и В разомкнуты, то х1=0, х2=0 и ясно, что связи между точками Р Q нет;→ f=0. С другой стороны, если переключатель А замкнут, а В разомкнут, то х1=1, х2=0 и связь между точками Р иQ осуществляется с помощью переключателя А,→f=1.
а)
б) г)
Булево Двоичное
сложение сложение
0+0=0 0+0=0
0+1=1 0+1=1
1+0=1 1+0=1
1+1=1 1+1=0 (перенос 1)
в)
Рис.10 а)-переключательная контактная схема функции ИЛИ
б)-таблица истинности функции ИЛИ
в)-правила двоичного и булевого сложения
г)-условное обозначение элемента ИЛИ
Функцию ИЛИ называют функцией логического сложения, дизъюнкцией
и записывают в виде; f=х1+х2 или f=х1 v х2. В цифровых системах функция,,ИЛИ'' реализуется с помощью электронной схемы, называемой элементом ИЛИ (условное обозначение которого приведено на рис.10 г).
Функция ИЛИ истинная, если истинен хотя бы один из её аргументов.
Исходя из этого определения дизъюнкции, можно указать её основные свойства:
1)результат многократного логического сложения некоторого аргумента с самим собой равен исходному аргументу: х+х+…+х=х;
2)логическая схема двух аргументов, из которых первой заведомо является ложным, равно второму аргументу: 0+х=х;
3)логическая схема двух аргументов, из которых один заведомо является истинным равно единице: 1+х=1;
 4)логическая сумма некоторого аргумента и его отрицания равна единице: х+х=1
4)логическая сумма некоторого аргумента и его отрицания равна единице: х+х=1
Основные законы булевой алгебры.
В булевой алгебре имеются четыре основных закона, регламентирующих порядок выполнения операций И, ИЛИ, НЕ в любом логическом выражении и обеспечивающих адекватное преобразование логических функций из одной формы в другую.
1. Переместительный закон справедлив как для дизъюнкции, так и для конъюнкции: от перемены мест слагаемых (сомножителей) их логическая сумма (произведение) не изменится. Так, для двух входных переменных можно записать: х1 + х2 = х2 + х1; х1 * х2 = х2 * х1 .
Переместительный закон будет справедлив при любом значении входных переменных.
2. Сочетательный закон также как и переместительный является симметричным:
а) при логическом сложении нескольких аргументов группу слагаемых можно заменить их логической суммой:
x1+x2+x3=x1+(x2+x3)=x2+(x1+x3)=x3+(x1+x2);
б) при логическом умножении нескольких аргументов группу сомножителей можно заменить их логическим произведением:
x1*x2*x3=x1*(x2*x3)=x2*(x1*x3)=x3*(x1*x2)
3. Распределительный закон.
а) распределительный закон 1-го рода: произведение суммы нескольких аргументов на какую-либо (логическую) переменную равно сумме произведений каждого слагаемого на эту переменную:
(x2+x3)*x1=x1*x2+x1*x3
б) распределительный закон П-го рода: сумма некоторой логической переменной и произведение нескольких аргументов равна произведению сумм каждого сомножителя этой переменной:
x1+x2x3=(x1+x2)*(x1+x3)
Док-во:
 (х1+х2)*(х1+х3)=х1*х1+х1*х3+х1*х2+х2*х3=х1+х1*х3+х1*х2+х2*х3=х1(1+х3+х2)+х2*х3=х1+х2*х3 —что и требовалось доказать 1
(х1+х2)*(х1+х3)=х1*х1+х1*х3+х1*х2+х2*х3=х1+х1*х3+х1*х2+х2*х3=х1(1+х3+х2)+х2*х3=х1+х2*х3 —что и требовалось доказать 1
4. Закон инверсии (правило Де Моргана), симметричен относительно дизъюнкции и конъюнкции:
а) отрицание логической суммы нескольких аргументов равно логическому произведению отрицаний этих же аргументов:



 х1+х2+…+хn=х1*х2*…*хn
х1+х2+…+хn=х1*х2*…*хn
Доказательство закона не представляет трудностей, т.к. условия обращения в нуль как левой, так и правой частей закона состоит в том, чтобы был истинным хотя бы один аргумент.



 б) отрицание логического произведения нескольких аргументов равно логической сумме отрицания этих же аргументов:
б) отрицание логического произведения нескольких аргументов равно логической сумме отрицания этих же аргументов:
x1*x2*…xn=x1+x2+…+xn
Справедливость этого закона следует из того, что условие обращения в единицу обеих частей заключается в том, чтобы был ложным хотя бы один аргумент из любого конечного их множества.
Следствие из законов булевой алгебры
Из рассмотренных выше законов выведем ряд следствий, которые сформулируем в виде правил.
1. Правило старшинства логических операций. По аналогии с арифметическими действиями будем считать отрицание – логическим действием первой ступени (старшей логической операцией), конъюнкцию – действием второй ступени, а дизъюнкцию – действием третьей ступени (младшей логической операцией).
2. 

 Правило склеивания обеспечивает упрощение логических выражений:
Правило склеивания обеспечивает упрощение логических выражений:
(x1+x2)*(x1+x2)=1 x1*(x1+x2)=x1


 x1*x1 +x1*x2+x1*x2+0=x1*(1+x2+x2)=x1 x1(x2+x2)=x1
x1*x1 +x1*x2+x1*x2+0=x1*(1+x2+x2)=x1 x1(x2+x2)=x1

 1 1
1 1
3. Правило поглощения также позволяет упростить выражения:
x1+x1*x2=x1 x1(x1+x2)=x1


 x1(1+x2)=x1 x1*x1 +x1*x2=x1(1+x2)=x1
x1(1+x2)=x1 x1*x1 +x1*x2=x1(1+x2)=x1
1 1 1
Канонические формы ФАЛ.
Важным этапом построения сложных дискретных устройств является определения способа соединения между собой логических элементов, обеспечивающих работу устройства в соответствии с заданным законом функционирования. Однако, любая функция алгебры логики выражается через исходные функции неоднозначно. Поэтому требуется найти такую форму её представления, которая позволяет построит наиболее простую электрическую схему. При решении этой задачи заданную функцию алгебры логики дискретного устройства вначале оказывается удобным представить в некоторой исходной канонической форме, которую называют нормальной.
Каноническими формами преставления функции алгебры логики является
СДНФ и СКНФ, ДНФ и КНФ.


 ДНФ –это дизъюнкция конечного числа элементарных конъюнкций. Конъюнкцию называют элементарной, если она представляет собой произведения переменных без скобок: например:
ДНФ –это дизъюнкция конечного числа элементарных конъюнкций. Конъюнкцию называют элементарной, если она представляет собой произведения переменных без скобок: например:
F(х1,…х4)=х1х2+х3х4+х1х3х4..

 Наряду с нормальными могут быть и другие дизъюнктивные формы. Например: дизъюнктивную форму х1х2+х2х3 нельзя назвать нормальной, т.к. х1х2 не является элементарной конъюнкцией.
Наряду с нормальными могут быть и другие дизъюнктивные формы. Например: дизъюнктивную форму х1х2+х2х3 нельзя назвать нормальной, т.к. х1х2 не является элементарной конъюнкцией.

 КНФ - это конъюнкция конечного числа элементарных дизъюнкций. Дизъюнкцию называют элементарной, если она представляет собой дизъюнкцию одиночных переменных или их инверсий. Например:F(х1…х4)=(х1+х3)(х1+х2+х4)(х2+х3)
КНФ - это конъюнкция конечного числа элементарных дизъюнкций. Дизъюнкцию называют элементарной, если она представляет собой дизъюнкцию одиночных переменных или их инверсий. Например:F(х1…х4)=(х1+х3)(х1+х2+х4)(х2+х3)

 Наряду с нормальными могут быть и другие конъюнктивные формы.
Наряду с нормальными могут быть и другие конъюнктивные формы.
Например, конъюнктивную форму (х1+х3)(х2+х3) нельзя назвать нормальной,
 т.к. х1+х3 не является элементарной дизъюнкцией. Любое логическое выражение может быть представлено в нормальной форме с помощью
т.к. х1+х3 не является элементарной дизъюнкцией. Любое логическое выражение может быть представлено в нормальной форме с помощью
следующих действий (преобразований):
1) в результате многократного применения законов инверсии снимаются
общие и групповые отрицания так чтобы отрицания остались только у одиночных переменных;
2) с помощью распределительных законов производятся переход к одной из
нормальных форм функции:
а) для перехода к ДНФ применяется распределительный закон первого рода
(раскрываются все скобки)
б) для перехода к КНФ применяется распределительный закон второго рода.
Пример 1. Представить в ДНФ функцию:







 Используя закон F=х2х3+(х1+х2)=х2х3*(х1+х2)=(х2+х3)(х1+х2)=
Используя закон F=х2х3+(х1+х2)=х2х3*(х1+х2)=(х2+х3)(х1+х2)=


 инверсии, получим =х1х2+х2*х2+х1х3+х2х3=
инверсии, получим =х1х2+х2*х2+х1х3+х2х3=




 Далее используем правило поглощения:
Далее используем правило поглощения:
 =х1х2+х2+х1х3+х2х3=х2+х1х3
=х1х2+х2+х1х3+х2х3=х2+х1х3
Пример2. Представить в КНФ функцию:





 F=х1+х1+х2+х3=х1+х1х2х3=(х1+х1)(х1+х2)(х1+х3)
F=х1+х1+х2+х3=х1+х1х2х3=(х1+х1)(х1+х2)(х1+х3)
Две другие канонические формы функции СДНФ и СКНФ являются исходными при минимизации ФАЛ. Поэтому очень важно уметь получать эти формы из таблицы истинности функции и из ДНФ и КНФ.
СДНФ – представляет собой алгебраическое выражение, которое принимает значение равное 1, на тех наборах переменных, на которых значение заданной функции равно 1.
СКНФ – представляет собой алгебраическое выражение, которое принимает значение 0 на тех наборах переменных, на которых значение заданной функции равно 0.
Рассмотрим такой пример. Пусть функция f (х1 х2 х3) задана таблицей истинности:
Табл. 3
Для нахождения СДНФ выбирают из табл.3 только те строки, на которых функция равна 1 (0, 4, 6, 7). В СДНФ записывают конъюнкции переменных в прямом виде, соответствующие выбранным строкам:





 х1х2х3, х1х2х3, х1х2х3, х1х2х3
х1х2х3, х1х2х3, х1х2х3, х1х2х3
Соединяя эти конъюнкции знаками дизъюнкции, окончательно получим:





 FСДНФ=х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3
FСДНФ=х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3


 Для получения из таблицы истинности СКНФ рассматриваем наборы переменных, на которых функция равна 0 (1, 2, 3, 5). Выписываем дизъюнкции, соответствующие этим наборам, причем в инверсном виде, т.е.
Для получения из таблицы истинности СКНФ рассматриваем наборы переменных, на которых функция равна 0 (1, 2, 3, 5). Выписываем дизъюнкции, соответствующие этим наборам, причем в инверсном виде, т.е.


 х1 +х2 +х3; х1+ х2 +х3; х1 +х2 +х3; х1 +х2 +х3;
х1 +х2 +х3; х1+ х2 +х3; х1 +х2 +х3; х1 +х2 +х3;
Все полученные дизъюнкции соединяем между собой знаками конъюнкций:





 F=(х1 +х2 +х3)* (х1 +х2 +х3)*(х1 +х2 +х3)*(х1 +х2 +х3)
F=(х1 +х2 +х3)* (х1 +х2 +х3)*(х1 +х2 +х3)*(х1 +х2 +х3)
Для перехода от ДНФ к СДФ в каждый из наборов, в которых представлены не все аргументы, следует ввести выражение вида
хi+хi(где хi- отсутствующая в наборе переменная).


 Так как хi+хi=1, то такая операция не изменяет значения функции.
Так как хi+хi=1, то такая операция не изменяет значения функции.



 Например: Получить СДНФ из ДНФ: FДНФ=х1+х2х3
Например: Получить СДНФ из ДНФ: FДНФ=х1+х2х3

















 F=х1*(х2 +х2)* (х3 +х3)+(х1+х1)*(х2 х3)=(x1*x2+x1 x2)*(x3*x3)+ х1х2х3+х1х2х3= х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3
F=х1*(х2 +х2)* (х3 +х3)+(х1+х1)*(х2 х3)=(x1*x2+x1 x2)*(x3*x3)+ х1х2х3+х1х2х3= х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3+ х1х2х3
Для перехода от КНФ к СКНФ к каждому набору не содержащему
Всех переменных, и инверсных значений отсутствующих переменных:
хi хi. Окончательное выражение для СКНФ получается после использования распределительного закона 2 рода и исключения лишних
наборов на основе закона повторения. Например: Получить СКНФ

 из КНФ: FКНФ=(х2 +х3)* (х1 +х3);
из КНФ: FКНФ=(х2 +х3)* (х1 +х3);


 FСКНФ=(х2 +х3)* (х1 +х3)= (x1*x1+x2+ x3)*(x1+x2*x2+x3)=(x1+x2+x3)* (x1+x2+x3)* (x1+x2+x3)*(x1+x2+x3)
FСКНФ=(х2 +х3)* (х1 +х3)= (x1*x1+x2+ x3)*(x1+x2*x2+x3)=(x1+x2+x3)* (x1+x2+x3)* (x1+x2+x3)*(x1+x2+x3)

 CДНФ и СКНФ – это разные формы записи одной и той же функции, т.е. они равны. Докажем это, пользуясь таблицей истинности функции логической неравнозначности:
CДНФ и СКНФ – это разные формы записи одной и той же функции, т.е. они равны. Докажем это, пользуясь таблицей истинности функции логической неравнозначности:
FСДНФ= х1х2+ х1х2










 FСКНФ=(х1 +х2)* (х1 +х2)= х1х1+ х1х2+ х1х2+ х1х2= х1х2+ х1х2
FСКНФ=(х1 +х2)* (х1 +х2)= х1х1+ х1х2+ х1х2+ х1х2= х1х2+ х1х2
0 0
Минимизация Ф А Л
При построении цифровых устр



 х2 Функция f (x1,x2,x3),заданная
х2 Функция f (x1,x2,x3),заданная
 таблицей истинности (табл. 2)
таблицей истинности (табл. 2)
 010 0 0 может быть задана графически.
010 0 0 может быть задана графически.




 110 0 111 1
110 0 111 1

 000 0 1 х3
000 0 1 х3



 100 0 0 101
100 0 0 101
 x2x3
x2x3 
 x1 00 01 11 10
x1 00 01 11 10 0 1 1
0 1 1
 x
x
 P Q
P Q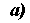


 б)
б)
 x1 & f
x1 & f

 х
х
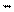


 x
x
 Рис.9 а) – переключательная схема функции f = х * х
Рис.9 а) – переключательная схема функции f = х * х б) – таблица истинности f = х * х
б) – таблица истинности f = х * х


 1
1


 На рис. 10 два переключателя А и В соединены параллельно и связывают точки Р и Q. Состояния переключателей и соединения Р Q выпрямляются с помощью булевых переменных х1, х2 и f соответственно. Если оба переключателя А и В разомкнуты, то х1=0, х2=0 и ясно, что связи между точками Р Q нет;→ f=0. С другой стороны, если переключатель А замкнут, а В разомкнут, то х1=1, х2=0 и связь между точками Р иQ осуществляется с помощью переключателя А,→f=1.
На рис. 10 два переключателя А и В соединены параллельно и связывают точки Р и Q. Состояния переключателей и соединения Р Q выпрямляются с помощью булевых переменных х1, х2 и f соответственно. Если оба переключателя А и В разомкнуты, то х1=0, х2=0 и ясно, что связи между точками Р Q нет;→ f=0. С другой стороны, если переключатель А замкнут, а В разомкнут, то х1=1, х2=0 и связь между точками Р иQ осуществляется с помощью переключателя А,→f=1.



 №
№
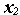
 4)логическая сумма некоторого аргумента и его отрицания равна единице: х+х=1
4)логическая сумма некоторого аргумента и его отрицания равна единице: х+х=1 (х1+х2)*(х1+х3)=х1*х1+х1*х3+х1*х2+х2*х3=х1+х1*х3+х1*х2+х2*х3=х1(1+х3+х2)+х2*х3=х1+х2*х3 —что и требовалось доказать 1
(х1+х2)*(х1+х3)=х1*х1+х1*х3+х1*х2+х2*х3=х1+х1*х3+х1*х2+х2*х3=х1(1+х3+х2)+х2*х3=х1+х2*х3 —что и требовалось доказать 1 х1+х2+…+хn=х1*х2*…*хn
х1+х2+…+хn=х1*х2*…*хn
 б) отрицание логического произведения нескольких аргументов равно логической сумме отрицания этих же аргументов:
б) отрицание логического произведения нескольких аргументов равно логической сумме отрицания этих же аргументов: Правило склеивания обеспечивает упрощение логических выражений:
Правило склеивания обеспечивает упрощение логических выражений: x1*x1 +x1*x2+x1*x2+0=x1*(1+x2+x2)=x1 x1(x2+x2)=x1
x1*x1 +x1*x2+x1*x2+0=x1*(1+x2+x2)=x1 x1(x2+x2)=x1
 1 1
1 1

 x1(1+x2)=x1 x1*x1 +x1*x2=x1(1+x2)=x1
x1(1+x2)=x1 x1*x1 +x1*x2=x1(1+x2)=x1

 Наряду с нормальными могут быть и другие дизъюнктивные формы. Например: дизъюнктивную форму х1х2+х2х3 нельзя назвать нормальной, т.к. х1х2 не является элементарной конъюнкцией.
Наряду с нормальными могут быть и другие дизъюнктивные формы. Например: дизъюнктивную форму х1х2+х2х3 нельзя назвать нормальной, т.к. х1х2 не является элементарной конъюнкцией.
 Наряду с нормальными могут быть и другие конъюнктивные формы.
Наряду с нормальными могут быть и другие конъюнктивные формы. т.к. х1+х3 не является элементарной дизъюнкцией. Любое логическое выражение может быть представлено в нормальной форме с помощью
т.к. х1+х3 не является элементарной дизъюнкцией. Любое логическое выражение может быть представлено в нормальной форме с помощью




 Далее используем правило поглощения:
Далее используем правило поглощения: =х1х2+х2+х1х3+х2х3=х2+х1х3
=х1х2+х2+х1х3+х2х3=х2+х1х3


 Так как хi+хi=1, то такая операция не изменяет значения функции.
Так как хi+хi=1, то такая операция не изменяет значения функции.





