Лабораторная работа 6.
VI. Дифференциальные уравнения. Ряды.
1. Ряды и произведения.
2. Аналитическое решение дифференциальных уравнений.
3. Численное решение дифференциальных уравнений.
§1. Ряды и произведения
Вычисление суммы ряда и произведений.
Конечные и бесконечные суммы 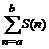 вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b.
вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b.
Если требуется вычислить сумму бесконечного ряда, то в качестве верхнего предела вводится infinity.
Аналогичным образом вычисляются произведения 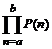 командами прямого product(P(n),n=a..b) и отложенного действий Product P(n),n=a..b).
командами прямого product(P(n),n=a..b) и отложенного действий Product P(n),n=a..b).
Задание 1.1.
1. Найти полную и N -частичную суммы ряда, общий член которого равен: an = 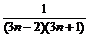 .
.
> restart: a[n]:=1/((3*n-2)*(3*n+1));
an:= 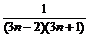
> S[N]:=Sum(a[n], n=1..N)=sum(a[n], n=1..N);
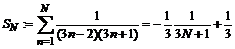
> S:=limit(rhs(S[N]), N=+infinity);
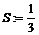
2. К какой функции сходится степенной ряд: 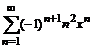 ?
?
> Sum((-1)^(n+1)*n^2*x^n, n=1..infinity)=
sum((-1)^(n+1)*n^2*x^n, n=1..infinity);
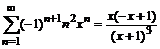 .
.
3. Найти сумму степенного ряда 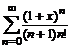 .
.
> Sum((1+x)^n/((n+1)*n!), n=0..infinity)=
sum((1+x)^n/((n+1)*n!), n=0..infinity);
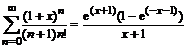
4. Вычислить бесконечное произведение: 
> Product(2/n,n=1..infinity)=
product(2/n, n=1..infinity);
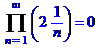
5.Вычислить произведение: 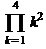
> Product(k^2, k=1..4)= product(k^2, k=1..4);
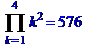
Разложение функции в степенной ряд и ряд Тейлора.
Разложение функции f (x) в степенной ряд в окрестности точки а
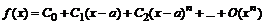
осуществляется командой series(f(x), x=a, n), где а – точка, в окрестности которой производится разложение, n – число членов ряда.
Аналогичного действия команда taylor(f(x), x=a, n) раскладывает функции f(x) в окрестности точки x=a до порядка n -1 по формуле Тейлора.
Команды series и taylor выдают результат, имеющий тип series. Для того, чтобы иметь возможность дальнейшей работы с полученным разложением, его следует преобразовать в полином с помощью команды convert(%,polynom).
Функцию многих переменных f (x 1,…, xn) можно разложить в ряд Тейлора по набору переменных (x 1,…, xn) в окрестности точки (a 1,…, an) до порядка n с помощью команды mtaylor(f(x), [x1,…,xn], n). Эта команда находится в стандартной библиотеке, поэтому перед использованием должна быть вызвана readlib(mtaylor).
Задание 1.2.
1. Разложить в степенной ряд 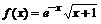 в окрестности х 0=0, удерживая 5 первых членов.
в окрестности х 0=0, удерживая 5 первых членов.
> f(x)=series(exp(-x)*sqrt(x+1), x=0, 5);
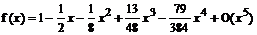
2. Построить на одном рисунке графики интеграла ошибок 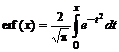 и его разложения в ряд Тейлора в окрестности нуля.
и его разложения в ряд Тейлора в окрестности нуля.
> taylor(erf(x),x,8): p:=convert(%,polynom);
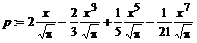
> plot({erf(x),p},x=-2..2,thickness=[2,2],
linestyle=[1,3], color=[red,green]);
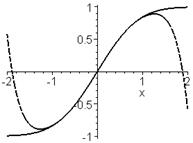
Пунктирной линей изображен график ряда Тейлора, а сплошной – самой функции.
3.Разложить 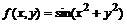 в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
> readlib(mtaylor):
> f=mtaylor(sin(x^2+y^2), [x=0,y=0], 7);
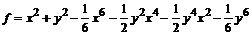
Задание 1.3.
1. Разложить в ряд Фурье функцию f (x)= x /2 с периодом 2p на интервале [0; 2p], удерживая 6 членов ряда. Построить на одном рисунке графики функции и ее n -частичной суммы ряда Фурье.
Сначала полностью наберите процедуру fourierseries, предложенную выше в теоретической части.
> f:=x/2:x1:=0:x2:=2*Pi:
> fr:=fourierseries(f,x,x1,x2,6);
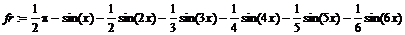
> plot({fr,f}, x=x1..x2, color=[blue,black],
thickness=2, linestyle=[3,1]);
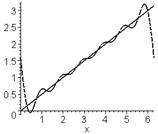
Пунктирной линией изображен график n -частичной суммы ряда Фурье, а сплошной – самой функции. По виду n -частичной суммы ряда Фурье в данном примере легко установить общий вид этого ряда:
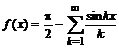 .
.
2. Разложить несколько раз в ряд Фурье функцию 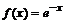 с периодом 2p на интервале [p;-p], удерживая 2, 4 и 8 членов ряда. Построить на одном рисунке графики функции и ее n -частичных сумм ряда Фурье.
с периодом 2p на интервале [p;-p], удерживая 2, 4 и 8 членов ряда. Построить на одном рисунке графики функции и ее n -частичных сумм ряда Фурье.
> f:=exp(-x);x1:=-Pi;x2:=Pi:
> fr1:=fourierseries(f,x,x1,x2,2):
> fr2:=fourierseries(f,x,x1,x2,4):
> fr3:=fourierseries(f,x,x1,x2,8):
> plot({f,fr1,fr2,fr3},x=x1..x2,color=[black, blue, green, red], thickness=2, linestyle= [1,3,2,2]);
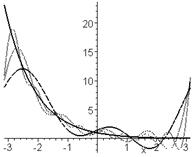
Сплошной линией изображен график функции, пунктирными – графики n -частичных сумм ряда Фурье. Видно, что чем больше слагаемых ряда удерживать, тем ближе расположен график суммы ряда к графику самой функции.
§2. Аналитическое решение дифференциальных уравнений
Задание 2.1.
1. Найти общее решение дифференциального уравнения y '+ y cos x =sin x cos x.
> restart;
> de:=diff(y(x),x)+y(x)*cos(x)=sin(x)*cos(x);
de: = 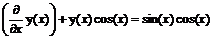
> dsolve(de,y(x));
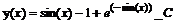 1
1
Итак, решение искомого уравнения есть функция 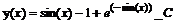 1.
1.
Замечание: при записи решения диффреренциального уравнения в Maple в строке вывода произвольная постоянная обозначена как _ С1.
2. Найти общее решение дифференциального уравнения второго порядка y ''-2 y '+ y =sin x + e - x .
> restart;
> deq:=diff(y(x),x$2)-2*diff(y(x),x)+y(x)
=sin(x)+exp(-x);
deq:= 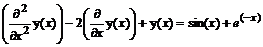
> dsolve(deq,y(x));
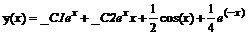
Замечание: так как исходное уравнение было второго порядка, то полученное решение содержит две произвольные константы, которые в Maple обычно обознаются как _ С1 и _ С2. Первые два слагаемых представляют собой общее решение соответствующего однородного дифференциального уравнения, а вторые два – частное решение неоднородного дифференциального уравнения.
3. Найти общее решение дифференциального уравнения порядка y ''+ k 2 y =sin(qx) в двух случаях: q ¹ k и q = k (резонанс).
> restart; de:=diff(y(x),x$2)+k^2*y(x)=sin(q*x);
dsolve(de,y(x));
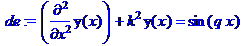
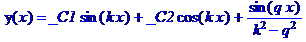
Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q = k.
> q:=k: dsolve(de,y(x));
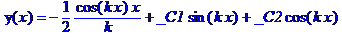
Замечание: в обоих случаях частное решение неоднородного уравнения и общее решение, содержащее произвольные постоянные, выводятся отдельными слагаемыми.
Задание 2.2.
Найти фундаментальную систему решений дифференциального уравнения: y (4)+2 y ''+ y =0.
> de:=diff(y(x),x$4)+2*diff(y(x),x$2)+y(x)=0;
de: = 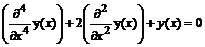
> dsolve(de, y(x), output=basis);
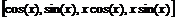
Решение задачи Коши или краевой задачи.
Команда dsolve может найти решение задачи Коши или краевой задачи, если помимо дифференциального уравнения задать начальные или краевые условия для неизвестной функции. Для обозначения производных в начальных или краевых условиях используется дифференциальный оператор 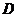 , например, условие y''(0)=2 следует записать в виде
, например, условие y''(0)=2 следует записать в виде 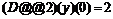 , или условие y '(1)=0:
, или условие y '(1)=0: 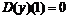 . Напомним, что производная n -го порядка записывается в виде
. Напомним, что производная n -го порядка записывается в виде 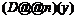 .
.
Задание 2.3.
1. Найти решение задачи Коши: y (4)+ y ''=2cos x, y (0)=-2, y '(0)=1, y ''(0)=0, y '''(0)=0.
> de:=diff(y(x),x$4)+diff(y(x),x$2)=2*cos(x);
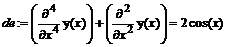
> cond:=y(0)=-2, D(y)(0)=1, (D@@2)(y)(0)=0,
(D@@3)(y)(0)=0;
cond:= y(0)=-2, D(y)(0)=1, (D(2))(y)(0)=0, (D(3))(y)(0)=0
> dsolve({de,cond},y(x));
y(x)=-2cos(x)- x sin(x)+ х
2. Найти решение краевой задачи: 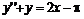 ,
, 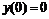 ,
, 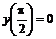 . Построить график решения.
. Построить график решения.
> restart; de:=diff(y(x),x$2)+y(x)=2*x-Pi;
de: = 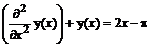
> cond:=y(0)=0,y(Pi/2)=0;
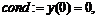
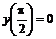
> dsolve({de,cond},y(x));
y(x)=2 x -p+pcos(x)
Замечание: для построения графика решения предварительно следует отделить правую часть полученного выражения.
> y1:=rhs(%):plot(y1,x=-10..20,thickness=2);

Задание 2.4.
Найти решение системы дифференциальных уравнений:
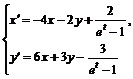
> sys:=diff(x(t),t)=-4*x(t)-2*y(t)+2/(exp(t)-1),
diff(y(t),t)=6*x(t)+3*y(t)-3/(exp(t)-1):
> dsolve({sys},{x(t),y(t)});
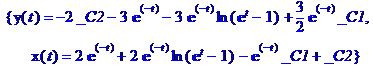
Найдены две функции x (t) и y (t), которые зависят от двух произвольных постоянных _ С1 и _ С2.
Задание 2.5.
1. Найти решение задачи Коши: 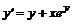 ,
, 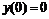 в виде степенного ряда с точностью до 5-го порядка.
в виде степенного ряда с точностью до 5-го порядка.
> restart; Order:=5:
> dsolve({diff(y(x),x)=y(x)+x*exp(y(x)),
y(0)=0}, y(x), type=series);
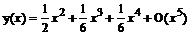
В полученном решении слагаемое 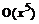 означает, что точность разложения была до 5-го порядка.
означает, что точность разложения была до 5-го порядка.
2. Найти общее решение дифференциального уравнения y ''(х)- y 3(х)= е-х cos x, в виде разложения в степенной ряд до 4-го порядка. Найти разложение при начальных условиях: y (0)=1, y '(0)=0.
> restart; Order:=4: de:=diff(y(x),x$2)-
y(x)^3=exp(-x)*cos(x):
> f:=dsolve(de,y(x),series);
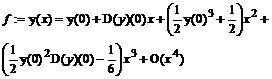
Замечание: в полученном разложении запись D(y)(0) обозначает производную в нуле: y '(0). Для нахождения частого решения осталось задать начальные условия:
> y(0):=1: D(y)(0):=0:f;
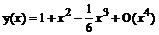
3. Найти приближенное решение в виде степенного ряда до 6-го порядка и точное решение задачи Коши: 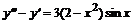 ,
, 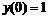 ,
, 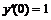 ,
, 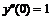 . Построить на одном рисунке графики точного и приближенного решений.
. Построить на одном рисунке графики точного и приближенного решений.
> restart; Order:=6:
> de:=diff(y(x),x$3)-diff(y(x),x)=
3*(2-x^2)*sin(x);
de: = 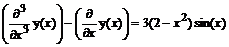
> cond:=y(0)=1, D(y)(0)=1, (D@@2)(y)(0)=1;
cond:=y(0)=1, D(y)(0)=1, D(2)(y)(0)=1
> dsolve({de,cond},y(x));
y(x)= 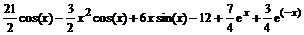
> y1:=rhs(%):
> dsolve({de,cond},y(x), series);
y(x)= 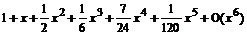
Замечание: тип решения дифференциального уравнения в виде ряда есть series, поэтому для дальнейшего использования такого решения (вычислений или построения графика) его обязательно следует конвертировать в полином с помощью команды convert
> convert(%,polynom): y2:=rhs(%):
> p1:=plot(y1,x=-3..3,thickness=2,color=black):
> p2:=plot(y2,x=-3..3, linestyle=3,thickness=2,
color=blue):
> with(plots): display(p1,p2);
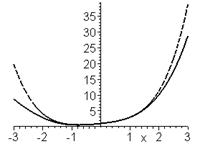
На этом рисунке видно, что наилучшее приближение точного решения степенным рядом достигается примерно на интервале -1< x <1.
Задание 3.1.
1. Найти численное и приближенное решение в виде степенного ряда до 6-ого порядка задачи Коши:  ,
, 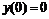 ,
,  .
.
Сначала найдем численное решение задачи Коши и построим его график.
> restart; Ordev=6:
> eq:=diff(y(x),x$2)-x*sin(y(x))=sin(2*x):
> cond:=y(0)=0, D(y)(0)=1:
> de:=dsolve({eq,cond},y(x),numeric);
de:= proc (rkf45_x)... end
Замечание: в строке вывода появляется сообщение о том, что при решении использован метод rkf45. Во избежание вывода строк, не несущих полезной информации, рекомендуется отделять промежуточные команды двоеточием. Если необходимо получить значение решения при каком-то фиксированном значении переменной х (заодно будет выведено значение производной решения в этой точке), например, при х =0.5, то следует набрать:
> de(0.5);

> with(plots):
> odeplot(de,[x,y(x)],-10..10,thickness=2);

Теперь найдем приближенное решение задачи Коши в виде степенного ряда и построим графики численного решения и полученного степенного ряда в интервале их наилучшего совпадения.
> dsolve({eq, cond}, y(x), series);

> convert(%, polynom):p:=rhs(%):
> p1:=odeplot(de,[x,y(x)],-2..3, thickness=2,
color=black):
> p2:=plot(p,x=-2..3,thickness=2,linestyle=3,
color=blue):
> display(p1,p2);

Наилучшее приближение решения степенным рядом достигается примерно на интервале -1< x <1 (так же как и в примере 3 задания 1.5).
2. Построить графики решений задачи Коши системы дифференциальных уравнений:
х '(t)=2 y (t)sin(t)- х (t)- t,
y '(t)= x (t),
х (0)=1, y (0)=2.
> restart; cond:=x(0)=1,y(0)=2:
> sys:=diff(x(t),t)=2*y(t)*sin(t)-x(t)-t,
diff(y(t),t)=x(t):
> F:=dsolve({sys,cond},[x(t),y(t)],numeric):
> with(plots):
> p1:=odeplot(F,[t,x(t)],-3..7, color=black,
thickness=2,linestyle=3):
> p2:=odeplot(F,[t,y(t)],-3..7,color=green,
thickness=2):
> p3:=textplot([3.5,8,"x(t)"], font=[TIMES,
ITALIC, 12]):
> p4:=textplot([5,13,"y(t)"], font=[TIMES,
ITALIC, 12]):
> display(p1,p2,p3,p4);

Пакет графического представления решений дифференциальных уравнений Detools.
Для численного решения задачи Коши, построения графиков решения и фазовых портретов в Maple имеется специальный пакет DEtools.
Команда DEplot из пакета DEtools строит численными методами графики решения или фазовые портреты. Эта команда аналогична команде odeplot, но более функциональна. Она, в отличие от odeplot, сама производит численное решение дифференциального уравнения. Основные параметры DEplot похожи на параметры odeplot: DEplot(de, vars, range, x=х1..х2, y=у1..у2, cond, ptions), где de - дифференциальное уравнение или система дифференциальных уравнений; vars – список неизвестных функций; range – диапазон измерения независимой переменной; cond – начальные условия; x=х1..х2 и y=у1..у2 – диапазоны изменения функций; options – дополнительные параметры.
Наиболее часто используемые параметры: linecolor =цвет линии; scene=[x,y] - определяет, какие зависимости выводить на график; iterations =число итераций, необходимое для повышения точности вычислений (по умолчанию это число равно 1); stepsize =число, равное расстоянию между точками на графике, по умолчанию оно равно (x2 - x1)/20, этот параметр необходим для вывода более гладкой кривой решения; obsrange = true / false - прерывать или нет вычисления, если график решения выходит за установленный для рисования интервал.
Для решения дифференциального уравнения n -ого порядка начальные условия можно задавать в более компактной форме: [x0, y0, y ' 0, y '' 0,…], где x0 - точка, в которой задаются начальные условия, y0 - значение искомой функции в точке x0, y ' 0, y '' 0,… - значения производных первой, второй и т.д. до (n -1)-ого порядка.
Задание 3.2.
Нарисовать график решения дифференциального уравнения: y²¢ cosx - y² + p y¢ = y - x,
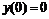 ,
,  ,
,  в интервале [-2,5; 1,4].
в интервале [-2,5; 1,4].
> restart; with(DEtools):
DEplot(cos(x)*diff(y(x),x$3)-diff(y(x),x$2)+Pi*diff(y(x),x)=y(x)-x,y(x),x=-2.5..1.4,[[y(0)=0,D(y)(0)=1,(D@@2)(y)(0)=1]],stepsize=.1,linecolor=black, thickness=2);

Контрольные задания.
При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:
 - число букв в фамилии студента,
- число букв в фамилии студента,
 - число букв в полном имени студента,
- число букв в полном имени студента,
 - число букв в отчестве студента.
- число букв в отчестве студента.
В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, отчество, фамилия).
1. Найти общее решение дифференциального уравнения:
а) 
б) 
2. Найти фундаментальную систему решений дифференциального уравнения:

3. Найти решение задачи Коши: 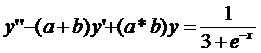 ,
, 
4. Найти решение системы дифференциальных уравнений:

при начальных условиях х (0)=1, х '(0)=0; у (0)=1.
5. Построить график численного решения задачи Коши
а) 
б) 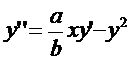 ,
, 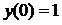 ,
,  .
.
6. Построить график численного решения задачи Коши  на интервале [-1.5; 3], используя команду DEplot.
на интервале [-1.5; 3], используя команду DEplot.
7. Найти сумму ряда и сумму первых N членов.
а) 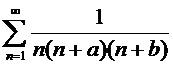 б)
б) 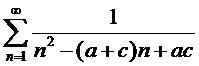
8. К какой функции сходится степенной ряд:  ?
?
9. Найти сумму степенного ряда  .
.
10. Вычислить бесконечное произведение: 
11. Вычислить произведение с точностью до 0,00001 
12. Разложить в степенной ряд  в окрестности x =0 до 11-ого порядка.
в окрестности x =0 до 11-ого порядка.
13. Разложить в ряд Тейлора функцию  до 6 – ого порядка в окрестности точки (0, 0).
до 6 – ого порядка в окрестности точки (0, 0).
Контрольные вопросы.
1. Какая команда позволяет решить дифференциальное уравнение? Опишите ее параметры.
2. С помощью каких операторов обозначается производная в дифференциальном уравнении и в начальных условиях?
3. Какой параметр команды dsolve следует установить, чтобы получить фундаментальную систему дифференциальных уравнений?
4. Какой параметр команды dsolve следует установить, чтобы получить приближенное решение дифференциального уравнения в виде разложения в степенной ряд? Как определяется порядок разложения?
5. Опишите, какие команды нужно ввести, прежде чем построить график приближенного решения, полученного в виде степенного ряда.
6. Какой параметр команды dsolve следует установить, чтобы решить дифференциальное уравнение численно?
7. Как найти значение решения дифференциального уравнения в какой-либо конкретной точке?
8. Какая команда позволяет построить график численно решенного дифференциального уравнения? В каком пакете находится эта команда?
9. Какой пакет предназначен для графического представления и численного решения дифференциального уравнения?
10. В чем отличие команд odeplot и DEplot?
11. Как вычислить сумму или произведение в Maple?
12. Какие команды осуществляют разложение функции в степенные ряды?
Лабораторная работа 6.
VI. Дифференциальные уравнения. Ряды.
1. Ряды и произведения.
2. Аналитическое решение дифференциальных уравнений.
3. Численное решение дифференциальных уравнений.
§1. Ряды и произведения



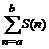 вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b.
вычисляются командой прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b.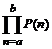 командами прямого product(P(n),n=a..b) и отложенного действий Product P(n),n=a..b).
командами прямого product(P(n),n=a..b) и отложенного действий Product P(n),n=a..b).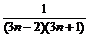 .
.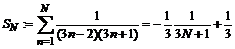
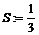
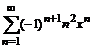 ?
?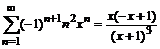 .
.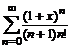 .
.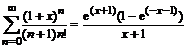

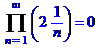
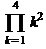
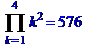
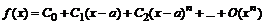
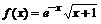 в окрестности х 0=0, удерживая 5 первых членов.
в окрестности х 0=0, удерживая 5 первых членов.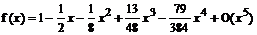
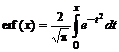 и его разложения в ряд Тейлора в окрестности нуля.
и его разложения в ряд Тейлора в окрестности нуля.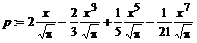

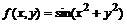 в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.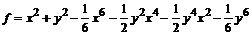
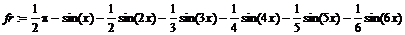

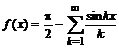 .
.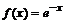 с периодом 2p на интервале [p;-p], удерживая 2, 4 и 8 членов ряда. Построить на одном рисунке графики функции и ее n -частичных сумм ряда Фурье.
с периодом 2p на интервале [p;-p], удерживая 2, 4 и 8 членов ряда. Построить на одном рисунке графики функции и ее n -частичных сумм ряда Фурье.
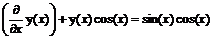
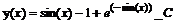 1
1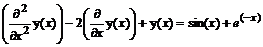
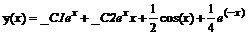
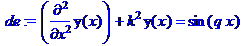
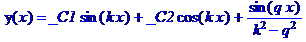
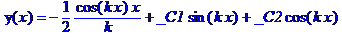
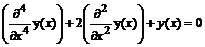
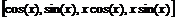
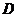 , например, условие y''(0)=2 следует записать в виде
, например, условие y''(0)=2 следует записать в виде 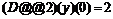 , или условие y '(1)=0:
, или условие y '(1)=0: 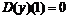 . Напомним, что производная n -го порядка записывается в виде
. Напомним, что производная n -го порядка записывается в виде 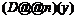 .
.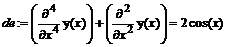
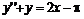 ,
, 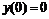 ,
, 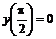 . Построить график решения.
. Построить график решения.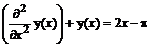
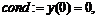

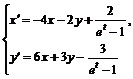
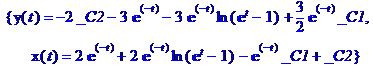
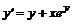 ,
, 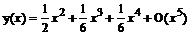
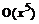 означает, что точность разложения была до 5-го порядка.
означает, что точность разложения была до 5-го порядка.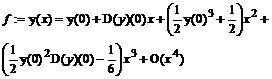
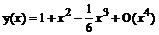
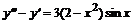 ,
, 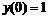 ,
, 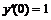 ,
, 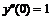 . Построить на одном рисунке графики точного и приближенного решений.
. Построить на одном рисунке графики точного и приближенного решений.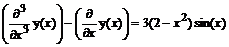
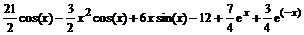
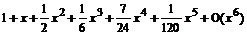

 ,
,  .
.




 в интервале [-2,5; 1,4].
в интервале [-2,5; 1,4].
 - число букв в фамилии студента,
- число букв в фамилии студента, - число букв в полном имени студента,
- число букв в полном имени студента, - число букв в отчестве студента.
- число букв в отчестве студента.


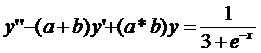 ,
, 


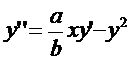 ,
, 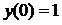 ,
,  .
. на интервале [-1.5; 3], используя команду DEplot.
на интервале [-1.5; 3], используя команду DEplot.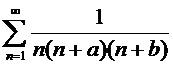 б)
б) 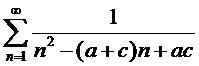
 ?
? .
.

 в окрестности x =0 до 11-ого порядка.
в окрестности x =0 до 11-ого порядка. до 6 – ого порядка в окрестности точки (0, 0).
до 6 – ого порядка в окрестности точки (0, 0).


