Навигация:

Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Новые материалы

Топ:

Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...

Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...

Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...

Интересное:

Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...

Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...

Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...

Дисциплины:

Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

Производная функция (определение, правило непосредственного нахождения производных)

2017-11-16

662

0.00 из 5.00 0 оценок

Заказать работу

Производной функцией в точке x₀ называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

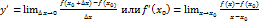
Производная функции f(x) есть некоторая функция f’(x), произведенная из данной функции.

Функция , имеющая производную в каждой точке интервала (a;b) называют дифференцируемой в этом интервале. Операция нахождения производной функции называется дифференцированием.

Значение производной функции в точке x=x₀ обозначается одним из символов:

Правило непосредственного нахождения производных:

· аргументу 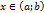дадим приращение ;

· найдем соответствующее приращение функции: ;

· составим отношение приращения функции к приращению аргумента: ;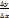

· найдем предел этого отношения при .

Если этот предел существует, то его называют производной функцией f(x) и обозначают одним из символов:

44. *Геометрический и механический смысл производной.

45. *Связь между непрерывностью и дифференцируемостью функций

46. *Основные теоремы о производных

Теорема(производная суммы): Производная суммы (разности) двух функций равна сумме (разности) производных этих функций:

Теорема(производная произведения):

Теорема(производная частного):

Пусть и тогда - сложная функция с промежуточным аргументом u и независимым аргументом х

Теорема(производная сложной функции):

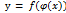Если функция имеет производную в точке х, а функция у = f(u) имеет производную у'_и в соответствующей точке , то сложная функция имеет производную в точке x₁, которая находится по формуле

Теорема(производная обратной функции):

Если функция 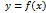строго монотонна на интервале (a;b) и имеет неравную нулю производную в произвольной точке интервала, то обратная ей функция также имеет производную 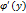в соответствующей точке, определяемую равенством или .

Дифференцирование функций, заданных неявно и параметрически.

Задана неявно:

Если функция задана уравнением у = f(x), разрешенным относительно y, то функция задана в явном виде.

Под неявным заданием функции понимают задание функции в виде уравнения , не разрешенного относительно y.

Алгоритм:

1) Дифференцируем заданное уравнение F(x,y)=0 по х, учитывая что х – независимая переменная, у – ее функция.

2) Результат дифференцирования разрешаем относительно искомой производной

Задана параметрически:

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений: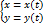

Найдем производную , считая, что функции имеют производные и что функция x=x(t) имеет обратную . По правилу дифференцирования обратной функции получаем: .

Функцию y=f(x) определяемую параметрическими уравнениями, можно рассматривать как сложную функцию

По правилу дифференцирования сложной функции имеем:

Получаем:

Поделиться с друзьями:

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...