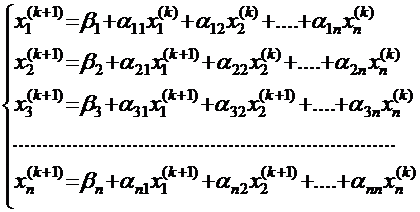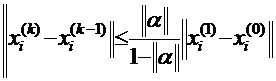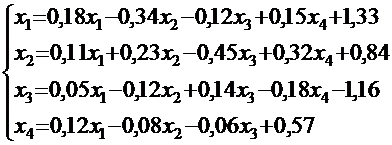Итерационные методы – приближённые методы решения систем уравнений. Главное – проверка выполнения условий сходимости итерационного процесса, а эти условия различны для систем, приведённых к каноническому виду, и для систем, не приведённых к каноническому виду.
Пусть система линейных уравнений приведена к каноническому (нормальному) виду, т. е. в векторной форме система имеет вид:
 ,
,
где  - вектор-столбец неизвестных,
- вектор-столбец неизвестных,
 - вектор-столбец свободных членов,
- вектор-столбец свободных членов,
 - матрица коэффициентов при неизвестных.
- матрица коэффициентов при неизвестных.
Эта же система в развёрнутом виде:

Сходимость итерационного процесса определяется нормами матрицы коэффициентов при неизвестных  : любая из трёх норм должна быть меньше единицы:
: любая из трёх норм должна быть меньше единицы:
 (1)
(1)
Для системы уравнений, не приведённой к каноническому виду, которая в векторной форме имеет вид:  , а в развёрнутом виде такова:
, а в развёрнутом виде такова:

обеспечение условий сходимости следует проверять, сравнивая модули диагональных элементов матрицы коэффициентов с суммой модулей остальных коэффициентов каждой строки:
 , где
, где  (2)
(2)
Если эти условия сходимости выполняются, то после приведения системы к каноническому виду и условия (1) будут выполнены, т. е. сходимость итерационного процесса обеспечена.
Метод простой итерации
После приведения системы уравнений к каноническому виду выбирают «нулевое» приближение – обычно столбец свободных членов, и каждое новое приближение вычисляют по предыдущему, руководствуясь формулой: 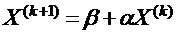
Вычисления следует закончить, когда 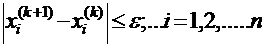
Пример 3. Методом простой итерации решить систему уравнений:
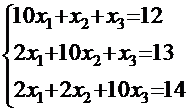
Условия сходимости (2) выполняются, значит, итерационный процесс будет сходиться. Приведём систему к каноническому виду, выразив 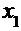 из первого уравнения,
из первого уравнения, 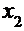 из второго,
из второго, 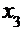 из третьего уравнения.
из третьего уравнения.
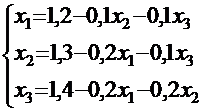
За «нулевое» приближение примем столбец свободных членов:
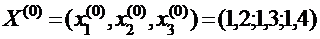
Подставляем в систему уравнений вектор «нулевого» приближения – получаем первое приближение:
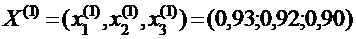
Продолжая этот процесс, получаем последовательность приближений:
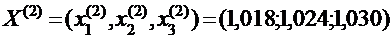
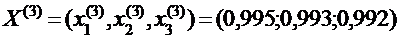
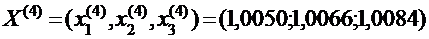
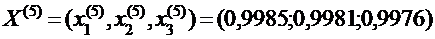
Корни получены с точностью до 10-2: 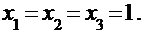 Из приведённой последовательности приближений видно, что приближённые значения корней колеблются вокруг точных значений.
Из приведённой последовательности приближений видно, что приближённые значения корней колеблются вокруг точных значений.
Процесс уточнения корней можно продолжить, если задана более высокая степень точности.
Итерационный метод Зейделя
Для ускорения процесса уточнения корней предложено усложнить вычислительную процедуру, включая в вычисления на каждой итерации приближённые значения корней, полученные на текущей итерации. Этот приём позволяет нередко решать системы, которые не решаются методом
простой итерации.
Условия сходимости метода Зейделя те же, что и для метода простой итерации. Их необходимо проверять перед началом расчёта.
Схема расчёта представлена в следующей системе уравнений:
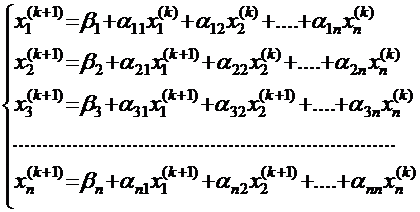
Расчёт следует продолжать до тех пор, пока не совпадут с заданной степенью точности два последовательных приближения каждого из корней системы уравнений.
Погрешность оценивается через нормы матрицы коэффициентов по формуле:
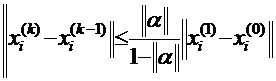
Пример 4. Методом Зейделя найти корни линейной системы уравнений с точностью до 10-3:
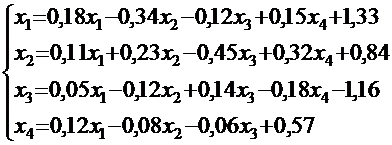
В качестве «нулевого» приближения взят столбец свободных членов, а результаты расчёта по схеме Зейделя приведены в таблице.
| Номер
итерации
|
X1
|
X2
|
X3
|
X4
|
|
| -1,6303
| 1,5583
| -1,6935
| 0,3974
|
|
| -1,8904
| 1,8797
| -1,7887
| 0,3862
|
|
| -2,0368
| 1,9768
| -1,8190
| 0,3746
|
|
| -2,0943
| 2,0027
| -1,8271
| 0,3693
|
|
| -2,1132
| 2,0085
| -1,8289
| 0,3674
|
|
| -2,1187
| 2,0095
| -1,8293
| 0,3668
|
|
| -2,1201
| 2,0095
| -1,8292
| 0,3666
|
|
| -2,1203
| 2,0094
| -1,8292
| 0,3666
|
|
| -2,1204
| 2,0094
| -1,8292
| 0,3666
|
|
| -2,1204
| 2,0094
| -1,8292
| 0,3666
|
Уточнения корней продолжались до тех пор, пока у корня X1 не совпали значащие цифры в 9-ой и 10-ой итерациях, а корни X2, X3 и X4 определены с заданной точностью на предыдущих итерациях.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2



 ,
, - вектор-столбец неизвестных,
- вектор-столбец неизвестных, - вектор-столбец свободных членов,
- вектор-столбец свободных членов, - матрица коэффициентов при неизвестных.
- матрица коэффициентов при неизвестных.
 (1)
(1) , а в развёрнутом виде такова:
, а в развёрнутом виде такова:
 , где
, где  (2)
(2)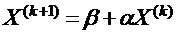
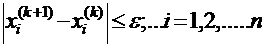
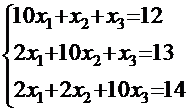
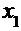 из первого уравнения,
из первого уравнения, 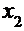 из второго,
из второго, 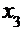 из третьего уравнения.
из третьего уравнения.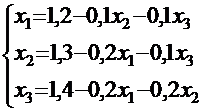
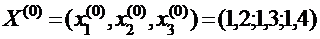
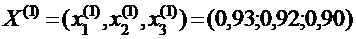
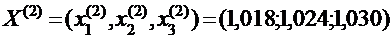
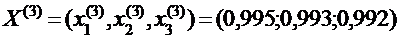
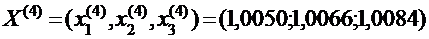
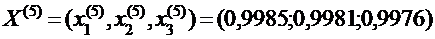
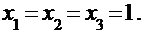 Из приведённой последовательности приближений видно, что приближённые значения корней колеблются вокруг точных значений.
Из приведённой последовательности приближений видно, что приближённые значения корней колеблются вокруг точных значений.