1) Если собственные векторы 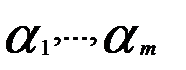 матрицы А принадлежат ее собственному значению
матрицы А принадлежат ее собственному значению 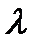 , т.е.
, т.е.  , то
, то 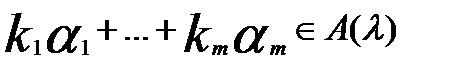 при любых числах
при любых числах 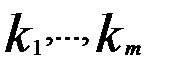 .
.
2) Если 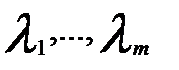 - попарно различные собственные значения матрицы А и векторы
- попарно различные собственные значения матрицы А и векторы 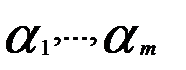 принадлежат собственно множествам A(
принадлежат собственно множествам A(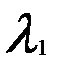 ),…,A(
),…,A(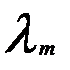 ), то из равенства
), то из равенства 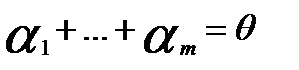 следует
следует 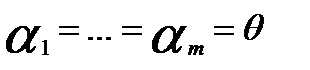
3)Пусть 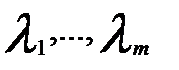 – попарно различные собственные значения матрицы А и в каждом из множеств A(
– попарно различные собственные значения матрицы А и в каждом из множеств A(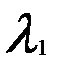 ),…,A(
),…,A(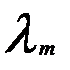 ) выбраны линейно независимые системы векторов
) выбраны линейно независимые системы векторов 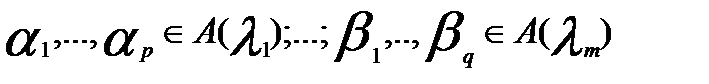 , тогда объединенная система векторов
, тогда объединенная система векторов 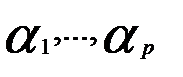 ,…,
,…, 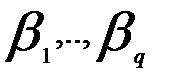 линейно независима.
линейно независима.
27)Квадратичной формой называется любой многочлен 2ой степени вида 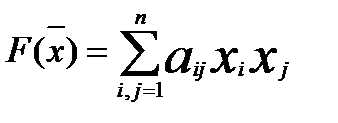 .
.
Закон инерции
Число слагаемых с положительными (отрицательными) коэффициентами в квадратичной форме канонического вида не зависит от линейного преобразования, приводящего к этому каноническому виду.
Критерий Сильвестра
а) Квадратичная форма положительно определена тогда и только тогда, когда все так называемые угловые миноры матрицы А положительны.
б) Квадратичная форма отрицательно определена тогда и только тогда, когда знаки её угловых миноров чередуются (
При нарушении а или б квадратичная форма будет знако-неопределенной.
30) Формула расстояния между точками в многомерном пространстве 
Дайте определение отрезка, сформулируйте теорему об отрезке(?).
Отрезок — множество точек, которое обычно изображается ограниченной частью прямой. Отрезок прямой, соединяющий две точки и (которые называются концами отрезка), обозначается следующим образом —АВ. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как модуль АВ.
Дайте определение k-мерной плоскости и гиперплоскости.
Арифметическим k-мерным пространством называется множество матриц-столбцов размера kx1, либо матриц-строк 1xk. а=(а1,а2,а3…аk) либо а=(тоже самое, записанное в столбик)
Гиперпло́скость — подпространство коразмерности 1 в векторном пространстве или проективном пространстве; то есть подпространство с размерностью, на единицу меньшей, чем объемлющее пространство.
Уравнение гиперплоскости
Пусть — нормальный вектор к гиперплоскости, тогда уравнение гиперплоскости, проходящей через точку 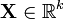 , имеет вид
, имеет вид 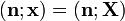
Здесь 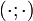 — скалярное произведение в пространстве. В частном случае уравнение принимает вид
— скалярное произведение в пространстве. В частном случае уравнение принимает вид 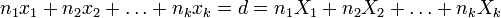
Дайте определение выпуклого множества и сформулируйте основные свойства
Выпуклых множеств.
Пусть  — векторное пространство (над полем вещественных чисел
— векторное пространство (над полем вещественных чисел  ).
).
Множество  называется выпуклым, если вместе с любыми двумя точками
называется выпуклым, если вместе с любыми двумя точками  множеству
множеству  принадлежат все точки отрезка
принадлежат все точки отрезка  , соединяющего в пространстве
, соединяющего в пространстве  точки
точки  и
и  . Этот отрезок можно представить как
. Этот отрезок можно представить как

 выпуклое
выпуклое  невыпуклое
невыпуклое
Свойства
Выпуклое множество в топологическом линейном пространстве является связным и линейно связным, гомотопически эквивалентным точке. В терминах связности, выпуклое множество можно определить так: множество выпукло, если его пересечение с любой (вещественной) прямой связно. Пусть  — выпуклое множество. Тогда для любых элементов
— выпуклое множество. Тогда для любых элементов 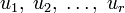 принадлежащих
принадлежащих  и для всех неотрицательных
и для всех неотрицательных  , таких что
, таких что  , вектор
, вектор  принадлежит
принадлежит  .
.
Вектор  называется выпуклой комбинацией элементов
называется выпуклой комбинацией элементов 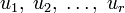 .
.
· Пересечение любого числа выпуклых множеств является выпуклым множеством, таким образом выпуклые подмножества образуют полную сетку. Это так же означает и то, что любое подмножество  линейного пространства содержится внутри малого выпуклого множества (называемого выпуклой оболочкой множества
линейного пространства содержится внутри малого выпуклого множества (называемого выпуклой оболочкой множества  ), то есть пересечение всех выпуклых множеств содержит
), то есть пересечение всех выпуклых множеств содержит  .
.
· Замкнутые выпуклые множества могут быть определены как пересечения замкнутых полупространств (множества точек в пространстве, которые лежат только на одной частигиперплоскости). Из выше сказанного становится понятным, что такие пересечения являются выпуклыми и замкнутыми множествами. Для доказательства обратного, то есть что каждое выпуклое множество может быть представлено в виде пересечения, можно использовать теорему об опорной гиперплоскости в форме в которой для данного замкнутого выпуклого множества 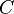 и точки
и точки  , не принадлежащей ему, существует замкнутое полупространство
, не принадлежащей ему, существует замкнутое полупространство  , содержащее
, содержащее 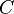 и не содержащее
и не содержащее  . Теорема об опорной гиперплоскости является частным случаем теоремы Хана — Банаха из функционального анализа.
. Теорема об опорной гиперплоскости является частным случаем теоремы Хана — Банаха из функционального анализа.
· Теорема Хелли: Предположим в конечном семействе выпуклых подмножеств  , пересечение любых
, пересечение любых 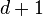 из них непусто. Тогда пересечение всех подмножеств из этого семейства непусто.
из них непусто. Тогда пересечение всех подмножеств из этого семейства непусто.
· Любое выпуклое множество единичной площади в  можно целиком заключить в некоторый треугольник площади 2.[1]
можно целиком заключить в некоторый треугольник площади 2.[1]



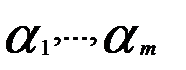 матрицы А принадлежат ее собственному значению
матрицы А принадлежат ее собственному значению 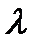 , т.е.
, т.е.  , то
, то 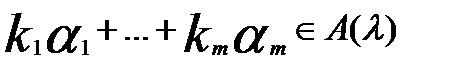 при любых числах
при любых числах 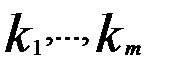 .
.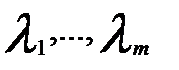 - попарно различные собственные значения матрицы А и векторы
- попарно различные собственные значения матрицы А и векторы 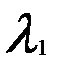 ),…,A(
),…,A(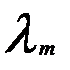 ), то из равенства
), то из равенства 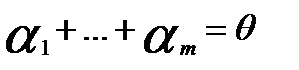 следует
следует 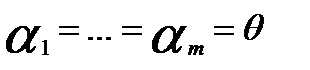
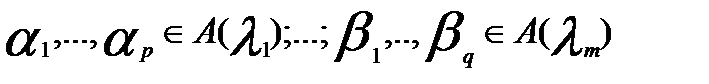 , тогда объединенная система векторов
, тогда объединенная система векторов 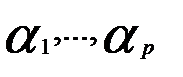 ,…,
,…, 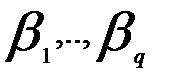 линейно независима.
линейно независима.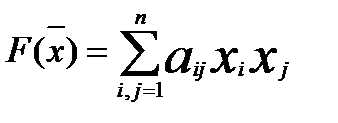 .
.

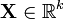 , имеет вид
, имеет вид 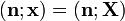
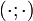 — скалярное произведение в пространстве. В частном случае уравнение принимает вид
— скалярное произведение в пространстве. В частном случае уравнение принимает вид 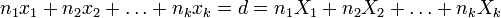
 — векторное пространство (над полем вещественных чисел
— векторное пространство (над полем вещественных чисел  ).
). называется выпуклым, если вместе с любыми двумя точками
называется выпуклым, если вместе с любыми двумя точками  множеству
множеству  принадлежат все точки отрезка
принадлежат все точки отрезка  , соединяющего в пространстве
, соединяющего в пространстве  и
и  . Этот отрезок можно представить как
. Этот отрезок можно представить как
 выпуклое
выпуклое  невыпуклое
невыпуклое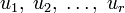 принадлежащих
принадлежащих  , таких что
, таких что  , вектор
, вектор  принадлежит
принадлежит  называется выпуклой комбинацией элементов
называется выпуклой комбинацией элементов 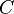 и точки
и точки  , не принадлежащей ему, существует замкнутое полупространство
, не принадлежащей ему, существует замкнутое полупространство  , содержащее
, содержащее  , пересечение любых
, пересечение любых 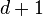 из них непусто. Тогда пересечение всех подмножеств из этого семейства непусто.
из них непусто. Тогда пересечение всех подмножеств из этого семейства непусто. можно целиком заключить в некоторый треугольник площади 2.[1]
можно целиком заключить в некоторый треугольник площади 2.[1]


