ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
I. Прямые и косвенные измерения
Измерить физическую величину – значит с помощью тех или иных технических средств сравнить ее с однородной величиной, принятой за единицу.
Все измерения можно разделить на прямые и косвенные. Прямым измерением физической величины называется определение ее размера непосредственно по прибору (примеры: измерение длины тела с помощью масштабной линейки, измерение температуры с помощью термометра, измерение времени с помощью секундомера). Косвенными измерениями называются вычисления размера физической величины на основании функциональной зависимости между ней и величинами, измеряемыми непосредственно (примеры: вычисление объема тела по его геометрическим размерам, средней скорости тела по пройденному расстоянию и времени, ускорения свободного падения по периоду колебаний математического маятника и его длине).
Таблица коэффициентов Стьюдента
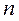
| 
|
| 0,1
| 0,3
| 0,5
| 0,7
| 0,8
| 0,9
| 0,95
| 0,98
| 0,99
| 0,999
|
|
| 0,16
| 0,5
| 1,00
| 2.0
| 3,1
| 6.3
| 12,7
| 31,8
| 63,7
| 636,6
|
|
| 0,14
| 0,45
| 0,82
| 1,3
| 1,9
| 2,9
| 4,3
| 7,0
| 9,9
| 31,6
|
|
| 0,14
| 0,42
| 0,77
| 1,3
| 1,6
| 2,4
| 3,2
| 4,5
| 5,8
| 12,9
|
|
| 0,13
| 0,41
| 0,74
| 1,2
| 1,5
| 2,1
| 2,8
| 3,7
| 4,6
| 8,6
|
|
| 0,13
| 0,41
| 0,73
| 1,2
| 1,5
| 2,0
| 2,6
| 3,4
| 4,0
| 6,9
|
|
| 0,13
| 0,40
| 0,72
| 1,1
| 1,4
| 1,9
| 2,4
| 3,1
| 3,7
| 6,0
|
|
| 0,13
| 0,40
| 0,71
| 1,1
| 1,4
| 1,9
| 2,4
| 3,0
| 3,5
| 5,4
|
|
| 0,13
| 0,40
| 0,71
| 1,1
| 1,4
| 1,9
| 2,3
| 2,9
| 3,4
| 5,0
|
|
| 0,13
| 0,40
| 0,70
| 1,1
| 1,4
| 1,8
| 2,3
| 2,8
| 3,3
| 4,8
|
Тогда абсолютная погрешность серии из 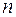 измерений равна
измерений равна  .Величина среднеквадратичной погрешности
.Величина среднеквадратичной погрешности  вычисляется по формуле:
вычисляется по формуле:  , где
, где 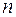 - число измерений;
- число измерений;  - абсолютные погрешности отдельных измерений, равные разности между отдельными и наиболее вероятным значением измеряемой величины
- абсолютные погрешности отдельных измерений, равные разности между отдельными и наиболее вероятным значением измеряемой величины  . За наиболее вероятное значение
. За наиболее вероятное значение  физической величины принимается среднее арифметическое значение из
физической величины принимается среднее арифметическое значение из 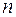 измерений:
измерений:  . При обработке измерений вычисляют и относительную погрешность
. При обработке измерений вычисляют и относительную погрешность 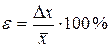 .
.
Схема обработки прямых измерений
- Находим среднее арифметическое
 из всех полученных значений
из всех полученных значений  измеряемой величины:
измеряемой величины:  .
. - Определяем абсолютные погрешности
 отдельных измерений:
отдельных измерений: 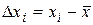 .
. - Вычисляем
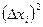 . Находим сумму
. Находим сумму  .
. 

- Определяем среднюю квадратичную погрешность среднего арифметического:
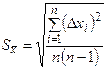 .
. - По заданному преподавателем коэффициенту надежности
 и числу измерений
и числу измерений 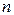 определяем по таблице коэффициент Стьюдента
определяем по таблице коэффициент Стьюдента  .
. - Находим величину абсолютной погрешности:
 .
. - Вычисляем относительную погрешность:
 .
. - Записываем окончательный результат в виде:

Пример применения схемы обработки прямых измерений
Рассмотрим прямые измерения толщины пластины  . Пусть заданы число измерений
. Пусть заданы число измерений  и коэффициент надежности
и коэффициент надежности 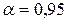 . Результаты измерений занесем в таблицу
. Результаты измерений занесем в таблицу

| 
| 
| 
|
|
| 2,32
| +0,01
| 0,0001
|
|
| 2,29
| -0,02
| 0,0004
|
|
| 2,32
| +0,01
| 0,0001
|
|
| 2,28
| -0,03
| 0,0009
|
|
| 2,33
| +0,02
| 0,0004
|
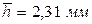
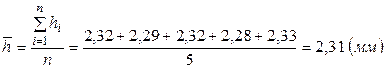 .
.  .
.
При  и
и  из таблицы находим
из таблицы находим  . Вычисляем
. Вычисляем  :
:
 .
.  . Окончательно:
. Окончательно:
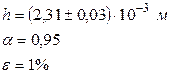
I.7. Пример применения схемы обработки косвенных измерений
Определяем объем прямого кругового цилиндра по формуле  , где
, где  - диаметр цилиндра,
- диаметр цилиндра,  - его высота, т.е. согласно ранее принятым обозначениям, имеем:
- его высота, т.е. согласно ранее принятым обозначениям, имеем:  . Непосредственно измеряем конечное число раз
. Непосредственно измеряем конечное число раз  и
и 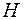 и обрабатываем их по схеме обработки прямых измерений. Вычисляем среднее значение объема:
и обрабатываем их по схеме обработки прямых измерений. Вычисляем среднее значение объема: 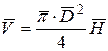 , здесь
, здесь  - среднеарифметические значения диаметра и высоты цилиндра;
- среднеарифметические значения диаметра и высоты цилиндра;  - среднее значение числа
- среднее значение числа  , определяемое как округленное значение этого числа с точностью до сотых, т.е.
, определяемое как округленное значение этого числа с точностью до сотых, т.е. 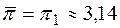 . Округленное значение числа
. Округленное значение числа  с точностью до тысячных равно
с точностью до тысячных равно  . Тогда для абсолютной погрешности представления числа
. Тогда для абсолютной погрешности представления числа  с точностью до сотых справедливо:
с точностью до сотых справедливо: 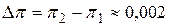 . Производим вспомогательные вычисления для определения относительной погрешности:
. Производим вспомогательные вычисления для определения относительной погрешности:  ;
;  ;
; 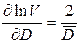 ;
;  . Записываем относительную погрешность косвенного измерения:
. Записываем относительную погрешность косвенного измерения:  . Определяем абсолютную погрешность:
. Определяем абсолютную погрешность:  и относительную погрешность, выраженную в процентах
и относительную погрешность, выраженную в процентах  .
.
Записываем результат в окончательном виде:
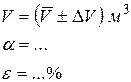
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Что такое измерение?
- Какие измерения являются прямыми?
- Какие измерения называются косвенными?
- На какие классы делятся погрешности?
- Что такое промахи? систематические ошибки? случайные ошибки?
- Можно ли провести абсолютно точные измерения?
- Можно ли устранить случайные ошибки?
- Постулаты Гаусса
- Что такое доверительный интервал?
- Что такое коэффициент надежности?
- Схема обработки прямых измерений
- Схема обработки косвенных измерений
- Что такое значащая цифра?
- Как округлять абсолютную погрешность?
- Как округлять среднее арифметическое значение измеряемой величины?
ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ



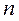

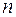 измерений равна
измерений равна  .Величина среднеквадратичной погрешности
.Величина среднеквадратичной погрешности  вычисляется по формуле:
вычисляется по формуле:  , где
, где  - абсолютные погрешности отдельных измерений, равные разности между отдельными и наиболее вероятным значением измеряемой величины
- абсолютные погрешности отдельных измерений, равные разности между отдельными и наиболее вероятным значением измеряемой величины  . За наиболее вероятное значение
. За наиболее вероятное значение  физической величины принимается среднее арифметическое значение из
физической величины принимается среднее арифметическое значение из  . При обработке измерений вычисляют и относительную погрешность
. При обработке измерений вычисляют и относительную погрешность 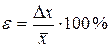 .
. измеряемой величины:
измеряемой величины:  .
. отдельных измерений:
отдельных измерений: 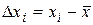 .
.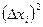 . Находим сумму
. Находим сумму  .
. 

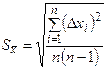 .
. и числу измерений
и числу измерений 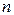 определяем по таблице коэффициент Стьюдента
определяем по таблице коэффициент Стьюдента  .
. .
. .
.
 . Пусть заданы число измерений
. Пусть заданы число измерений  и коэффициент надежности
и коэффициент надежности 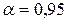 . Результаты измерений занесем в таблицу
. Результаты измерений занесем в таблицу



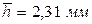
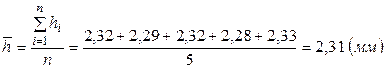 .
.  .
. из таблицы находим
из таблицы находим  . Вычисляем
. Вычисляем  :
: .
.  . Окончательно:
. Окончательно: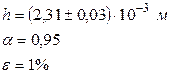
 , где
, где  - диаметр цилиндра,
- диаметр цилиндра,  - его высота, т.е. согласно ранее принятым обозначениям, имеем:
- его высота, т.е. согласно ранее принятым обозначениям, имеем:  . Непосредственно измеряем конечное число раз
. Непосредственно измеряем конечное число раз  и
и 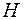 и обрабатываем их по схеме обработки прямых измерений. Вычисляем среднее значение объема:
и обрабатываем их по схеме обработки прямых измерений. Вычисляем среднее значение объема: 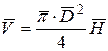 , здесь
, здесь  - среднеарифметические значения диаметра и высоты цилиндра;
- среднеарифметические значения диаметра и высоты цилиндра;  - среднее значение числа
- среднее значение числа  , определяемое как округленное значение этого числа с точностью до сотых, т.е.
, определяемое как округленное значение этого числа с точностью до сотых, т.е. 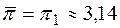 . Округленное значение числа
. Округленное значение числа  . Тогда для абсолютной погрешности представления числа
. Тогда для абсолютной погрешности представления числа 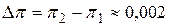 . Производим вспомогательные вычисления для определения относительной погрешности:
. Производим вспомогательные вычисления для определения относительной погрешности:  ;
;  ;
; 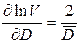 ;
;  . Записываем относительную погрешность косвенного измерения:
. Записываем относительную погрешность косвенного измерения:  . Определяем абсолютную погрешность:
. Определяем абсолютную погрешность:  и относительную погрешность, выраженную в процентах
и относительную погрешность, выраженную в процентах  .
.