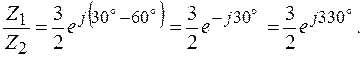КОМПЛЕКСНЫЕ ЧИСЛА
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
для студентов уровня ССО заочной формы обучения
всех специальностей
Минск 2006
Составитель Н.Н. Чемерко
Рецензент Т.К. Гресюк
Издание утверждено на заседании кафедры М и Ф
20 марта 2006 г., протокол №8
Зав. кафедрой Л.Л. Гладков
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
Комплексным числом называется выражение вида
 ,
,
где 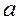 и
и 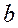 - действительные числа,
- действительные числа,
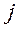 - мнимая единица.
- мнимая единица.
Число 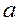 называется действительной частью комплексного числа, а число
называется действительной частью комплексного числа, а число 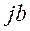 - мнимой частью.
- мнимой частью.
Комплексное число обозначается буквой 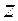 , множество комплексных чисел обозначается буквой
, множество комплексных чисел обозначается буквой 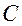 . Квадрат мнимой единицы равен
. Квадрат мнимой единицы равен 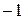 , то есть
, то есть 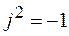 .
.
Запись комплексного числа 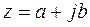 называется алгебраической формой.
называется алгебраической формой.
Два комплексных числа называются равными, когда равны их действительные части и коэффициенты при мнимой части, то есть
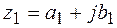 и
и 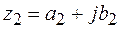
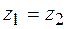 , если
, если 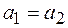 и
и 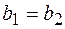 .
.
Понятие «больше» и «меньше» для комплексных чисел не определяются.
Число вида  называется нулем.
называется нулем.
Число вида 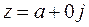 отождествляется с действительным числом
отождествляется с действительным числом 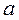 , то есть
, то есть 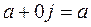 .
.
Комплексное число 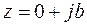 называется чисто мнимым и обозначается
называется чисто мнимым и обозначается 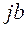 , то есть
, то есть 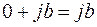 .
.
Комплексные числа 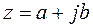 и
и 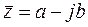 называются сопряженными.
называются сопряженными.
Произведение комплексных множителей имеет вид
 .
.
Сумма
Суммой двух комплексных чисел 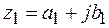 и
и 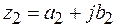 называется комплексное число
называется комплексное число
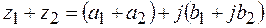 .
.
Произведение
Произведением двух комплексных чисел 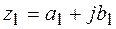 и
и 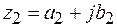 называется комплексное число
называется комплексное число
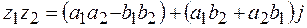 .
.
Выведем данную формулу
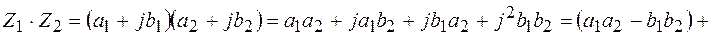
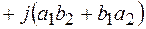 , то есть используем правило произведения многочлена на многочлен и заменяем
, то есть используем правило произведения многочлена на многочлен и заменяем 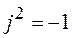 .
.
Вычитание
Вычитание вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел 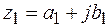 и
и 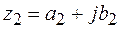 определяется формулами
определяется формулами
 ,
,
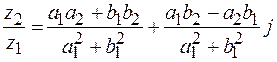 ,
,
где 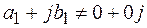 .
.
Докажем данную формулу. Для этого числитель и знаменатель умножим на число, сопряженное знаменателю и учитываем, что 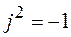
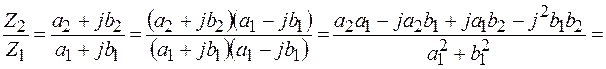
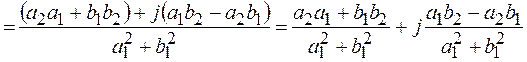 .
.
Формулы, определяющие правила действия над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия на двучленами 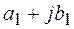 и
и 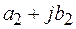 и заменить
и заменить 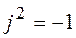 .
.
Деление
При делении комплексных чисел достаточно умножить числитель и знаменатель дроби 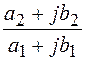 на число, сопряженное знаменателю, то есть на
на число, сопряженное знаменателю, то есть на 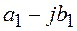 .
.
Возведение в степень
Возведение комплексного числа в степень производится по формулам возведение двучлена в степень, но при этом надо учитывать, что
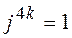 ;
; 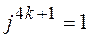 ;
; 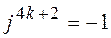 ;
; 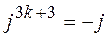 .
.
Умножение
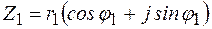





При умножении комплексных чисел в тригонометрической и показательной форме модули их перемножаются, а аргументы складываются

Пример 2.4

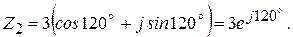
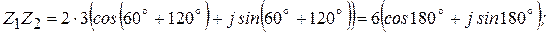
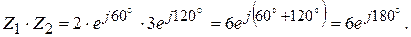
Деление


Таким образом, при делении комплексных чисел их модули делятся, а аргументы вычитаются
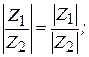

Пример 2.5
 ;
;  .
.

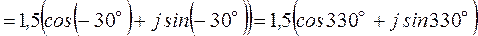 ;
;
ЛИТЕРАТУРА
1 Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука, 1980. – Гл. 10. – ÍÍ1-9.
2 Лисичкин В.Т., Соловейчик И.Л. Математика. Учебное пособие для техникумов. – М.: Высшая школа, 1991. – Гл. 2. – ÍÍ2-8.
3 Яковлев Г.Н. Алгебра и начала анализа, часть II. – М.: Наука, 1981. – Гл. 1. – ÍÍ1-3.
СОДЕРЖАНИЕ
1 ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ. 3
1.1 Сумма. 3
1.2 Произведение. 3
1.3 Вычитание. 4
1.4 Деление. 4
1.5 Возведение в степень. 4
1.6 Геометрическая интерпретация комплексного числа. 5
1.7 Поворот вектора комплексного числа. 5
Задание для самостоятельной работы. 7
2 ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФОРМЕ. 8
2.1 Умножение. 10
2.2 Деление. 10
2.3 Возведение комплексного числа в степень. 11
2.4 Корень n-ой степени из комплексного числа. 11
2.5 Переход от показательной и тригонометрической формы в алгебраическую 12
Решение примеров. 12
Задание для самостоятельной работы. 14
Литература……………………………………………………………………………………..15
План 2005/2006, поз.
Чемерко Нина Николаевна
КОМПЛЕКСНЫЕ ЧИСЛА
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
для студентов уровня ССО заочной формы обучения
всех специальностей
Редактор Н.В. Вердыш
Подписано к печати ___________
Формат 60х84/16
Усл. печ. л ___, уч.-изд. л. ___
Тираж ___ экз. Заказ ____
Учреждение образования
«ВЫСШИЙ ГОСУДАРСТВЕННЫЙ КОЛЛЕДЖ СВЯЗИ»
220114, г. Минск, ул. Ф. Скорины 8, к. 2
КОМПЛЕКСНЫЕ ЧИСЛА
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
«ВЫСШАЯ МАТЕМАТИКА»
для студентов уровня ССО заочной формы обучения
всех специальностей
Минск 2006
Составитель Н.Н. Чемерко
Рецензент Т.К. Гресюк
Издание утверждено на заседании кафедры М и Ф
20 марта 2006 г., протокол №8
Зав. кафедрой Л.Л. Гладков
ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
Комплексным числом называется выражение вида
 ,
,
где 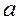 и
и 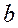 - действительные числа,
- действительные числа,
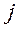 - мнимая единица.
- мнимая единица.
Число 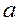 называется действительной частью комплексного числа, а число
называется действительной частью комплексного числа, а число 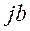 - мнимой частью.
- мнимой частью.
Комплексное число обозначается буквой 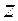 , множество комплексных чисел обозначается буквой
, множество комплексных чисел обозначается буквой 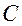 . Квадрат мнимой единицы равен
. Квадрат мнимой единицы равен 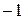 , то есть
, то есть 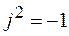 .
.
Запись комплексного числа 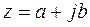 называется алгебраической формой.
называется алгебраической формой.
Два комплексных числа называются равными, когда равны их действительные части и коэффициенты при мнимой части, то есть
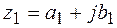 и
и 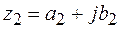
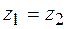 , если
, если 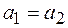 и
и 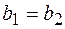 .
.
Понятие «больше» и «меньше» для комплексных чисел не определяются.
Число вида  называется нулем.
называется нулем.
Число вида 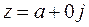 отождествляется с действительным числом
отождествляется с действительным числом 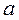 , то есть
, то есть 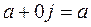 .
.
Комплексное число 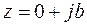 называется чисто мнимым и обозначается
называется чисто мнимым и обозначается 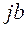 , то есть
, то есть 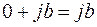 .
.
Комплексные числа 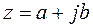 и
и 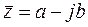 называются сопряженными.
называются сопряженными.
Произведение комплексных множителей имеет вид
 .
.
Сумма
Суммой двух комплексных чисел 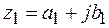 и
и 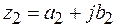 называется комплексное число
называется комплексное число
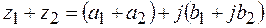 .
.
Произведение
Произведением двух комплексных чисел 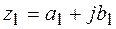 и
и 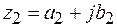 называется комплексное число
называется комплексное число
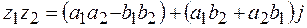 .
.
Выведем данную формулу
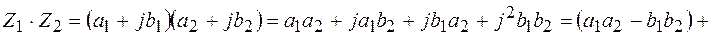
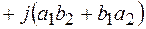 , то есть используем правило произведения многочлена на многочлен и заменяем
, то есть используем правило произведения многочлена на многочлен и заменяем 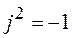 .
.
Вычитание
Вычитание вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел 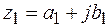 и
и 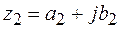 определяется формулами
определяется формулами
 ,
,
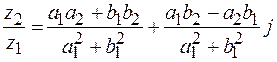 ,
,
где 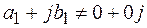 .
.
Докажем данную формулу. Для этого числитель и знаменатель умножим на число, сопряженное знаменателю и учитываем, что 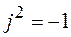
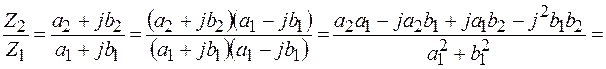
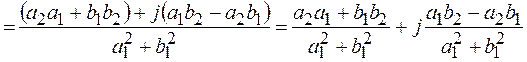 .
.
Формулы, определяющие правила действия над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия на двучленами 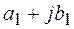 и
и 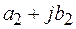 и заменить
и заменить 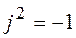 .
.
Деление
При делении комплексных чисел достаточно умножить числитель и знаменатель дроби 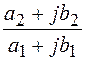 на число, сопряженное знаменателю, то есть на
на число, сопряженное знаменателю, то есть на 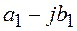 .
.
Возведение в степень
Возведение комплексного числа в степень производится по формулам возведение двучлена в степень, но при этом надо учитывать, что
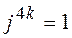 ;
; 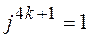 ;
; 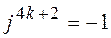 ;
; 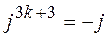 .
.



 ,
,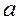 и
и 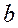 - действительные числа,
- действительные числа,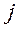 - мнимая единица.
- мнимая единица.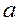 называется действительной частью комплексного числа, а число
называется действительной частью комплексного числа, а число 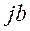 - мнимой частью.
- мнимой частью.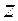 , множество комплексных чисел обозначается буквой
, множество комплексных чисел обозначается буквой 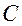 . Квадрат мнимой единицы равен
. Квадрат мнимой единицы равен 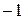 , то есть
, то есть 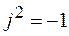 .
.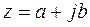 называется алгебраической формой.
называется алгебраической формой.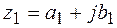 и
и 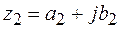
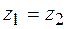 , если
, если 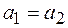 и
и 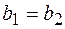 .
. называется нулем.
называется нулем.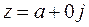 отождествляется с действительным числом
отождествляется с действительным числом 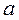 , то есть
, то есть 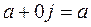 .
.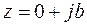 называется чисто мнимым и обозначается
называется чисто мнимым и обозначается 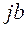 , то есть
, то есть 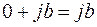 .
.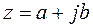 и
и 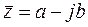 называются сопряженными.
называются сопряженными. .
.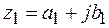 и
и 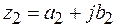 называется комплексное число
называется комплексное число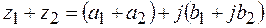 .
.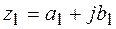 и
и 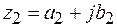 называется комплексное число
называется комплексное число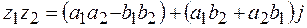 .
.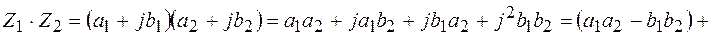
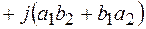 , то есть используем правило произведения многочлена на многочлен и заменяем
, то есть используем правило произведения многочлена на многочлен и заменяем 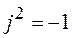 .
.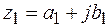 и
и  ,
,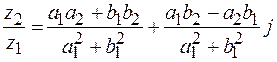 ,
,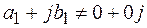 .
.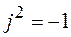
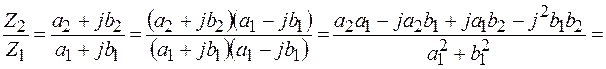
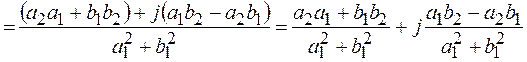 .
.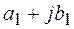 и
и 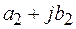 и заменить
и заменить 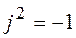 .
.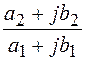 на число, сопряженное знаменателю, то есть на
на число, сопряженное знаменателю, то есть на 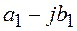 .
.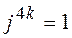 ;
; 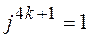 ;
; 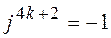 ;
; 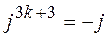 .
.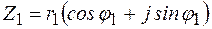







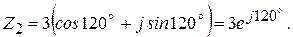
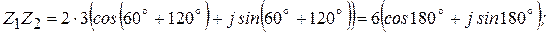
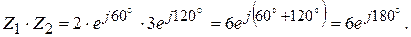


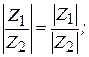

 ;
;  .
.
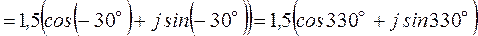 ;
;