Значение настроечных параметров для объектов с самовыравниванием

 

Закон регулирования	Типовой процесс регулирования
апериодический	20 %-ное перерегулирование	с минимальной квадратической площадью отклонения min ∫ y2(t)dt
И
П
ПИ
ПИД

Примечание: При расчете настроечных параметров необходимо также указать типовой переходный процесс и закон регулирования, для которых производится вычисление.

 

Указания к разделу «Системы автоматического

Управления на базе типовых логических контроллеров»

 

Логические функции могут быть заданы в виде таблиц истинности, в аналитической форме и в виде карт Карно.

Таблицы истинности отражают однозначное соответствие дискретных состояний входов и выходов автоматического дискретного устройства управления. При числе входов n (число переменных) возможны N = 2 ⁿ сочетаний комбинаций переменных. Так как последовательность смены комбинаций здесь роли не играет, то в таблице истинности их удобно располагать в виде кодов натурального ряда двоичных чисел:

 

0000 + 1 = 0001; 0000 + 1 = 0010; 0010 + 1 = 0011 и т. д.

 

При этом необходимо отметить, что не все комбинации состояний переменных реально будут иметь место. В этом случае значение функции, соответствующее этим наборам, записывается знаком несовместимости (~).

Ниже приведена таблица истинности для 4-х переменных (таблица 2.2).

 

Таблица 2.2

Таблица истинности

Номер комбинации	a	b	c	d	f (a,b,c,d)

 

Для получения аналитического выражения функции записывают исходные формы переключательной функции в виде совершенной дизъюнктивной (СДНФ) или конъюнктивной (СКНФ) нормальной формы.

СДНФ представляет собой дизъюнкцию (сумму) минтермов, а СКНФ – конъюнкцию (произведение) макстермов.

Минтермом или конституентой единицы для данного числа переменных называется всякая конъюнкция всех переменных, взятых по одной с инверсией или без нее. Если взять какой-либо конкретный набор переменных, то минтерм на этом наборе переменных строится следующим образом: каждая переменная в конъюнкцию входит с инверсией, если значение переменной равно нулю в данном наборе, или без инверсии, если значение переменной в наборе равно единице.

Макстермом или конституентой нуля для данного числа переменных называется всякая дизъюнкция всех переменных, взятых по одной с инверсией или без нее. Для конкретного набора переменных конституента нуля на этом наборе переменных строится следующим образом: каждая переменная в дизъюнкцию входит без инверсии, если в этом наборе переменная равно нулю, и с инверсией, если в этом наборе переменная равна единице.

Если функция задана таблицей, где указаны все наборы логических переменных и ее значения на них, то переход к аналитической форме осуществляется следующим образом: на основании таблицы записывается дизъюнкция конституент единиц тех наборов, на которых функция равна единице.

Суть метода карт Карно заключается в табличном представлении минтермов СДНФ. Карта Карно – это таблица с числом ячеек, равным числу наборов аргументов. В каждую ячейку можно вписать один набор (минтерм), причем смежные минтермы должны быть в соседних клетках. Смежные минтермы – это такие, которые отличаются знаком только одного аргумента. Соседство таких минтермов обеспечивается специальным подбором их для каждой ячейки. В каждую клетку карты записывается значение функции на данном наборе.

 

Суть методики составления карт Карно заключается в следующем:

1. Число клеток карты равно числу наборов аргументов (N =2 ⁿ).

2. Аргументы разбиваются на две равные или неравные группы аргументов.

3. Для одной группы (первые номера) отводятся столбцы таблицы, для другой (последние номера) – строки.

4. Прямое инверсное значение аргумента определяется двоичной цифровой маркировкой столбцов и строк.

 

На рис. 2.3 представлен пример составления карты Карно по таблице истинности.

			I 13
		6 V 1
IV 11	1		16 II 1	1
	III 1

 

Рис. 2.3. Составление карты Карно

 

Если логическая функция задана с помощью карт Карно, то переход к аналитическому выражению с использованием конституент единицы осуществляется следующим образом:

- для каждой клетки, в которой функция имеет значение 1, записывается конъюнкция всех входных переменных (прямых или инверсных), соответствующих этой клетке (конституента единицы).

- составляется дизъюнкция этих конституент единицы.

Если функция задана картой Карно, то ее аналитическое выражение может быть получено не только с помощью конституент единицы, но и более компактной форме. В этом и заключается основное преимущество карт Карно по сравнению с табличным заданием функции. Для этого используют следующие правила:

1. Все единицы должны быть заключены в прямоугольные контуры. Единичные контуры могут объединять несколько соседних единиц, но не должны содержать внутри себя нулей. Напомним, что соседние клетки не обязательно располагаются рядом. Одноименные контуры могут накладываться друг на друга, т. е. одна и та же единица может входить в несколько единичных контуров. При объединении контуры клетки, примыкающие к противоположным границам карты Карно, считаются соседними. Вообще, соседними считаются клетки, расположенные симметрично относительно границы любой переменной (границей переменной считается линия в карте Карно, которая отделяет прямое значение переменной от ее инверсного значения). Такие клетки также могут объединяться в прямоугольные контуры.

2. Площадь любого контура должна быть симметрична относительно границ переменных, пересекающих этот контур. Число клеток в контуре может быть 1, 2, 4, 8, 16, 32, …, 2 ⁿ.

Например, для составленной нами карты Карно (см. рис. 2.3) в контуры I, II, III включены клетки, каждая из которых является соседней с рядом расположенными. Требования прямоугольности контуров и количества клеток в них выполняются. В контур IV включены клетки, примыкающие к противоположным границам карты Карно и являющиеся также соседними. Контуры III и IV, II и IV перекрываются, что также не противоречит правилу, по которому одна клетка может входить в несколько контуров. Пересечение контуров означает тавтологию минтерма:

 

;

 

.

 

Контур V включает всего 1 клетку, так как соседних с ней клеток нет.

3. Каждой единичной клетке соответствует конъюнкция входных переменных, определяющих данную клетку, т.е. конституента единицы.

4. В контуре, объединяющем две клетки, одна из переменных меняет свое значение, поэтому алгебраическое выражение для контура из двух клеток не зависит от этой переменной, а представляется конъюнкцией всех других переменных. То же самое относится к контурам, охватывающим 4, 8, 16 и т.д. клеток. Таким образом, выражения, соответствующие контурам, не содержат тех переменных, чьи границы пересекаются площадью данного контура. Охватывая единичные клетки контурами, мы проводим склеивание соседних минтермов. Контуру из двух клеток соответствует одноступенчатое склеивание, из четырех – двухступенчатое и т. д. Так для контура I выражение функции запишется, если применить закон склеивания:

 

.

Для контура IV, включающего 4 клетки, выражение функции запишется следующим образом:

 

.

5. Выражение записывается как дизъюнкция конъюнкций, соответствующих выделенным на карте единичным контурам. Согласно этому правилу запишем аналитическое выражение функции, заданной картой Карно (см. рис. 2.3), с использованием выделенных единичных контуров:

 

Если значение функции для какого-либо набора неизвестное или невозможное (знак несовместимости ~), то из соображения наилучшей минимизации в клетках карты Карно с этим знаком можно проставить 0 или 1.

 

На основе полученной структурной формулы автомата строится его логическая схема на элементах, реализующих логические операции «AND», «OR» и «NOT», которая дает картину условий работы всего дискретного автомата без учета конкретного типа логических элементов (рис. 2.4 и 2.5).

Логическая схема строится с использованием обозначения элементов по ГОСТ 21.208-2013.

 

А

N

D

А

B

C

X

O

Входы

Выход

«OR»

«NOT»

Входы

Выход

NOT

А

O

А

Входы

B

C

X

OR

O

Выход

«AND»

 

Рис. 2.4. Графические изображения логических элементов в схемах

NOT

NOT

NOT

NOT

А

N

D

А

N

D

А

N

D

А

N

D

А

N

D

OR

acd

acd

acd

abcd

bc

b

a

c

d

o

Рис. 2.5. Логическая схема дискретного автомата, реализующая выражение

логической функции F (a, b, c, d)
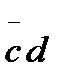