

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Прикладная механика
учебно-методическое пособие
для выполнения контрольных работ
для студентов очного и заочного обучения
специальности «Пожарная безопасность»
Астрахань – 2013
Учебно-методическое пособие предназначено для изучения дисциплины «Прикладная механика». Содержит краткие теоретические материалы по рассматриваемым разделам, подробную методику решения задач, типовые задания для студентов очного и заочного обучения специальности «Пожарная безопасность». – Астрахань, 2013.– 83 с.
Утверждено на заседании кафедры «Прикладная механика и графика»
Протокол № 3 от 14 октября 2013г.
Согласовано с УМУ АИСИ
«22» октября 2013 А.В. Мирошниченко
Рекомендовано к рассмотрению на методсовете специальности «Пожарная безопасность» АИСИ
Протокол № 1 от «25» октября 2013
Составители:
Хохлова Ольга Александровна, кандидат технических наук, доцент кафедры ПМГ
Синельщикова Оксана Николаевна, старший преподаватель кафедры ПМГ
Рецензенты:
Пономарева Екатерина Владимировна, кандидат физико-математических наук, доцент кафедры «Инженерная графика и механика» Астраханского государственного технического университета
Кокарев Александр Михайлович, кандидат технических наук, зав. кафедрой «Промышленное и гражданское строительство» АИСИ
© Хохлова О.А., Синельщикова О.Н.
© ГАОУ АО ВПО «Астраханский инженерно-строительный институт»
Содержание
Введение…………………………………………………………………………….4
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МАШИН И МЕХАНИЗМОВ……………..5
1. СТРУКТУРНЫЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ…………………..6
1.1. Классификация кинематических пар……………………………………….7
|
|
1.2. Кинематические цепи……………………………………………………….10
1.3. Определение класса плоских механизмов………………………………...12
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКОГО РЫЧАЖНОГО
МЕХАНИЗМА 2-ГО КЛАССА……………………………………………………14
2.1. Метод плана положений……………………………………………………...15
2.2. Метод планов скоростей……………………………………………………..16
2.3. Теорема подобия для плана скоростей………………………………………18
2.4. Метод планов ускорений……………………………………………………..21
2.5. Теорема подобия для плана ускорений……………………………………...23
3. КИНЕТОСТАТИКА ПЛОСКОГО РЫЧАЖНОГО МЕХАНИЗМА
2-ГО КЛАССА……………………………………………………………………...28
3.1. Принцип Даламбера для материальной точки……………………………....29
3.2. Принцип Даламбера для несвободной механической системы…………....30
3.3. Определение инерциальной нагрузки звеньев механизма………………....31
3.4. Графо-аналитический метод кинетостатического расчета структурных
групп 2-го класса…………………………………………………………………...36
3.5. Аналитический метод кинетостатического расчета структурных
групп 2-го класса……………………………………………………………..…….43
3.6. Определение уравновешивающей силы методом Жуковского…………....46
3.7. Расчет на прочность при сложном сопротивлении: плоском изгибе с
растяжением (сжатием)…………………………………………………………….49
УСЛОВИЕ И ВАРИАНТЫ ЗАДАНИЙ для контрольной работы №4
студентов очного отделения…………………………………………………….…55
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ №1 и №2для студентов
3-го курса заочного отделения…………………………………………………….66
Список литературы…………………………………………………………………83
Введение
Согласно Федеральному Государственному Образовательному Стандарту Высшего Профессионального образования по специальности 280705 «Пожарная безопасность» специалист в результате изучения данного раздела курса «Прикладная механика» должен:
знать: основы механики деформируемого твердого тела;
|
|
уметь: применять основные методики расчетов на прочность типовых элементов конструкций;
владеть: навыками работы с учебной и научной литературой при решении практических задач механики.
Предлагаемое учебное пособие подготовлено для студентов специальности 280705 «Пожарная безопасность» второго курса очного и третьего курса заочного отделений с учетом вышеперечисленных требований.
Пособие предназначено для формирования у студентов общих представлений о методах анализа, расчета и проектирования деталей и узлов механических систем, а также знаний и навыков, которые помогут им успешно осваивать последующие профилирующие дисциплины и решать практические инженерные задачи.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ МАШИН И МЕХАНИЗМОВ
Теория механизмов и машин – наука об общих методах исследования механизмов и машин, являющейся одной из основных машиностроительных дисциплин формирующих современного инженера.
Машина – устройство, создаваемое человеком и выполняющее механическое движение для преобразования энергии, материалов, информации. Основной признак машины – совершение некоторой полезной работы.
Классификация машин
В зависимости от функционального назначения различают:
1) Энергетические машины, преобразующие любой вид энергии в механическую и наоборот. К энергетическим машинам относятся двигатели внутреннего сгорания, электродвигатели, электрогенераторы, турбины и другие устройства.
2) Технологические и транспортные машины, которые преобразуют материалы, изменяют свойства, форму, состояние и положение объектов труда. К ним относятся металлообрабатывающие станки, прокатные станки, полиграфические, горные и текстильные машины, самолёты, автомобили, поезда, транспортёры, подъёмники ит.д.
3) Информационные машины, предназначенные для получения и преобразования информации. Информационные машины выполняют контрольно-измерительные операции, функции регулирования и управления технологическими процессами.
Машины, как правило, используются в виде совокупности, системы машины. В классическом исполнении такая система состоит из машины-двигателя, передаточного механизма и рабочей машины. Система нескольких взаимодействующих машин, связанных конструктивно, называется машинным агрегатом.
|
|
Основу каждой машины составляет устройство или группа устройств, называемых механизмами. Механизм – система тел, предназначенных для преобразования независимого движения одного или нескольких тел в требуемое движение остальных тел в соответствии с функциональным назначением.
Механизмы независимо от функционального назначения и конструктивного исполнения имеют общую структурную основу. Они состоят из звеньев – тел, участвующих в преобразовании движения.
Все механизмы можно разделить на плоские и пространственные. У плоского механизма точки его звеньев описывают траектории, лежащие в параллельных плоскостях. У пространственных механизмов точки его звеньев описывают неплоские траектории, лежащие в пересекающихся плоскостях.
Звено механизма – деталь или группа жёстко соединенных между собой деталей (твёрдое звено). Звенья могут быть гибкими (тросы, ремни и цепи), жидкими и газообразными.
Стойка – неподвижное звено или звено, условно принимаемое за неподвижное. Стойкой может быть станина, корпус, плата механизма и т.д. Относительно стойки оцениваются параметры движения механизма (перемещения, скорости и т.д.)
Из подвижных звеньев в зависимости от их расположения в цепи механизма выделяют входные и выходные звенья. Выходным звеном называется звено, которому сообщается движение от двигателя; выходным – звено, совершающее движение, для выполнения которого предназначен механизм. Остальные подвижные звенья механизма называются промежуточными. Механизмы могут иметь несколько входных и выходных звеньев.
Входное звено является ведущим звеном. Остальные подвижные звенья механизма называются ведомыми.
Кинематические цепи
Кинематической цепью называется совокупность звеньев, соединенных в кинематические пары. Кинематические цепи подразделяются на простые, сложные, замкнутые, незамкнутые.
Простой кинематической цепью называется такая цепь, у которой каждое звено входит не более чем в две кинематические пары (рис. 1.3). Кривошипно-шатунный механизм состоит из неподвижного звена – стойки и трех подвижных звеньев – 1, 2, 3. Кинематическими парами данного механизма будут 0-1, 1-2, 2-3, 3-0. Каждое звено входит в две кинематические пары, следовательно – это простая кинематическая цепь.
|
|

Рис. 1.3. Кинематическая схема кривошипно-шатунного механизма
Сложной называется такая кинематическая цепь, у которой хотя бы одно звено входит более чем в две кинематические пары (рис. 1.1). В данном механизме звено 2 входит в следующие кинематические пары: 1-2, 2-3, 2-4.
Замкнутой кинематической цепью называется цепь, каждое звено которой входит, по крайней мере, в две кинематические пары (рис. 1.1, 1.3).
Незамкнутой называется кинематическая цепь, у которой есть звенья, входящие только в одну кинематическую пару. На рис. 1.4 звено 5 входит только в одну кинематическую пару: 4-5.

Рис. 1.4. Кинематическая схема манипулятора
Кинематическая схема механизма дает полное представление о структуре механизма и определяет его кинематические свойства. Она выполняется графическим способом с использованием условных обозначений звеньев, кинематических пар и указанием размеров, которые необходимы для кинематического анализа механизма.
На кинематических схемах механизмов звенья изображаются отрезками прямых и нумеруются арабскими цифрами. Кинематические пары обозначаются заглавными буквами латинского алфавита и схематически изображаются так, как показано на рис. 1.3, 1.4.
Для проектируемого механизма необходимо знать какое количество звеньев, связанных со стойкой, должно быть ведущим для того, чтобы движение механизма было вполне определенным. Для этого вычисляют число степеней свободы W механизма относительно стойки, которое показывает количество ведущих звеньев. Большинство механизмов, используемых в технике, имеют число степеней свободы, равное единице и, следовательно, должны иметь одно ведущее звено.
Рис. 1.6.
4.2) Кулиса 3 и ползун 2 образуют группу Ассура2-го класса с двумя вращательными и одной поступательной кинематическими парами (рис. 1.6. б).
4.3) Шатун 4 и ползун 5 образуют группу Ассура2-го класса с двумя вращательными и одной поступательной кинематическими парами (рис. 1.6. в).
Таким образом, механизм входят одна группа Ассура1-го класса и две группы Ассура2-го класса.
5) Представленный механизм является плоским механизмом 2-го класса.
Рис. 2.4
3. Построим план скоростей (рис. 2.4 б):
– из произвольной точки  проведем луч, перпендикулярный ОА, в направлении вращения кривошипа 1 и отложим на нем отрезок
проведем луч, перпендикулярный ОА, в направлении вращения кривошипа 1 и отложим на нем отрезок 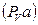 произвольной длины;
произвольной длины;
– через точку а проведем прямую, перпендикулярную АВ, а через полюс  – прямую, параллельную оси Ох;
– прямую, параллельную оси Ох;
– на пересечении этих прямых получим точку b. Вектор  – скорость точки В в масштабе
– скорость точки В в масштабе  .
.
4. Определим скорость точки С шатуна 2. На основании теоремы о скоростях точек тела, совершающего плоскопараллельное движение, составим два векторных равенства:
|
|
 ;
;  ,
,
где  –скорость точки С, относительно точки А во вращательном движении шатуна 2 вокруг А; следовательно, вектор
–скорость точки С, относительно точки А во вращательном движении шатуна 2 вокруг А; следовательно, вектор 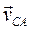 перпендикулярен отрезку АС;
перпендикулярен отрезку АС;
 – скорость точки С, относительно точки В во вращательном движении шатуна 2 вокруг В; следовательно, вектор
– скорость точки С, относительно точки В во вращательном движении шатуна 2 вокруг В; следовательно, вектор  перпендикулярен отрезку ВС.
перпендикулярен отрезку ВС.
5. На плане скоростей через точку а проведем прямую, перпендикулярную АС, а через точку b – прямую, перпендикулярную ВС. Их пересечение дает точку с.
В результате построений мы получили на плане скоростей треугольник abc, подобный треугольнику АВС плана механизма. Признак подобия – взаимная перпендикулярность сторон. Таким образом, п.4 и 5 являются непосредственным доказательством теоремы подобия для плана скоростей.
Соединим точку с с полюсом плана скоростей. Вектор  – скорость точки С в масштабе
– скорость точки С в масштабе  .
.
Пример №3. Построить по исходным данным план скоростей механизма, представленного на рис. 2.5 а и определить скорости всех указанных точек, а также угловые скорости звеньев.
Дано:  ,
, 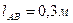 ,
,  ,
,  ,
,  ,
,  .
.
Построить план скоростей механизма и определить:  ,
, 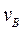 ,
,  ,
,  ,
, 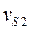 ,
,  .
.
Решение:
Скорость точки А определяем по формуле (2.3):
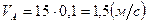 .
.
На плане скоростей строим отрезок  . Тогда масштабный коэффициент скорости по формуле (2.5) будет равен:
. Тогда масштабный коэффициент скорости по формуле (2.5) будет равен:  .
.
По теореме о сложении скоростей скорость точки B равна  . Из точки а на плане скоростей проводим луч, перпендикулярный АВ, соответствующий вектору скорости
. Из точки а на плане скоростей проводим луч, перпендикулярный АВ, соответствующий вектору скорости  , а из полюса
, а из полюса  проводим луч, параллельный ОВ, т.е. параллельный ходу движения ползуна, соответствующий вектору скорости
проводим луч, параллельный ОВ, т.е. параллельный ходу движения ползуна, соответствующий вектору скорости  . Точка пересечения лучей b соответствует концу вектора скорости точки В. Строим план скоростей (рис 2.5 б).
. Точка пересечения лучей b соответствует концу вектора скорости точки В. Строим план скоростей (рис 2.5 б).
Для того чтобы определить численное значение точки В, воспользуемся формулой (2.6):
 .
.
Найдем скорости остальных точек. Поскольку все точки звеньев совершают плоскопараллельное движение, то воспользуемся теоремой подобия для плана скоростей. Рассмотрим точку S2. Она принадлежит звену 2 и делит шатун АВ посередине. На плане скоростей точка s2 также будет делить отрезок аb пополам. Расстояние от полюса  до s2 и будет определять скорость точки S2.
до s2 и будет определять скорость точки S2.
Точка С тоже принадлежит звену 2 и расположена на расстоянии  . На плане скоростей она так же будет отстоять от точка а на расстоянии
. На плане скоростей она так же будет отстоять от точка а на расстоянии  . Соединяем полюс и точку с – этот и есть вектор скорости точки С.
. Соединяем полюс и точку с – этот и есть вектор скорости точки С.
Рассмотрим точку D. Она принадлежит звену 1. Порядок определения скорости точки D аналогичен точке С. План скоростей построен.
После определения направлений скоростей точек на плане скоростей, определим численное значение скоростей точек аналогично определению численного значения скорости точки В:
 ,
,
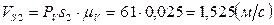 ,
,
 .
.

Рис. 2.5
Угловую скорость движения шатуна 2 определяем по формуле (2.7):
 .
.
Проверим правильность построения плана скоростей (рис. 2.5 в). Для того чтобы узнать направления скоростей точек звена 2, построим мгновенный центр скоростей (МЦС): направление и значение скорости точки А нам известно, а также известна траектория движения ползуна В. По направлению вектора скорости точки А определяем направление угловой скорости шатуна 2 –  . Соединив МЦС с точками S 2 и С, находим направления векторов скоростей этих точек, согласно направлению
. Соединив МЦС с точками S 2 и С, находим направления векторов скоростей этих точек, согласно направлению  . Направление скорости точки D перпендикулярно кривошипу 1 и направлено в сторону его вращения.
. Направление скорости точки D перпендикулярно кривошипу 1 и направлено в сторону его вращения.
Из построений видно, что направления векторов скоростей обоих методов совпадают.
2.4. Метод планов ускорений
Для построения плана ускорений для заданного на рис. 2.2 положения механизма составим векторные уравнения, связывающие ускорения точек звеньев механизма.
Ускорение точки А принадлежащей кривошипу 1, вращающегося с постоянной угловой скоростью  определяется формулой:
определяется формулой:
 , (2.8)
, (2.8)
где  – вектор нормального ускорения точки А;
– вектор нормального ускорения точки А;
 – вектор касательного ускорения точки А.
– вектор касательного ускорения точки А.
Нормальное ускорение всегда направлено от точки к центру вращения (в нашем случает от точки А к центру О) и определяется формулой:
 . (2.9)
. (2.9)
Касательное ускорение всегда направлено по касательной к траектории движения точки и выражается формулой:
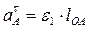 , (2.10)
, (2.10)
где  – угловое ускорение кривошипа 1.
– угловое ускорение кривошипа 1.
По условию задачи кривошип вращается равномерно, т.е.  , следовательно, здесь (и в последующих примерах) его угловое ускорение равно нулю:
, следовательно, здесь (и в последующих примерах) его угловое ускорение равно нулю:  .
.
Подставляя (2.9) и (2.10) в уравнение (2.8) получаем:
 . (2.11)
. (2.11)
При построении планов ускорений используют масштабный коэффициент ускорения 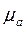 , который определяется формулой:
, который определяется формулой:
 , (2.12)
, (2.12)
где  – значение ускорения точки А, полученное по формуле (2.11);
– значение ускорения точки А, полученное по формуле (2.11);
 – расстояние на плане ускорений от полюса
– расстояние на плане ускорений от полюса  до точки а (выбирается самостоятельно в соответствии с форматом чертежа, мм).
до точки а (выбирается самостоятельно в соответствии с форматом чертежа, мм).
Поскольку точка В движется плоскопараллельно, то ускорение точки В равно сумме ускорения полюса и ускорения данной точки во вращательном движении вокруг полюса:
 , (2.13)
, (2.13)
где 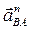 – вектор нормального ускорения точки В относительно полюса А;
– вектор нормального ускорения точки В относительно полюса А;  – вектор касательного ускорения точки В относительно полюса А;
– вектор касательного ускорения точки В относительно полюса А;
 – вектор ускорения точки В относительно стойки О.
– вектор ускорения точки В относительно стойки О.
Нормальное ускорение 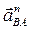 направлено вдоль АВ от точки В к центру вращения – полюсу А и определяется формулой:
направлено вдоль АВ от точки В к центру вращения – полюсу А и определяется формулой:
 . (2.14)
. (2.14)
Величина отрезка на плане ускорений, соответствующего значению  , определяется формулой:
, определяется формулой:
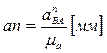 . (2.15)
. (2.15)
Касательное ускорение всегда направлено по касательной к траектории движения точки (перпендикулярно АВ) и выражается формулой:
 ,
,
где  – угловое ускорение шатуна 2 (оно пока не известно).
– угловое ускорение шатуна 2 (оно пока не известно).
Поскольку ползун В движется поступательно, то вектор ускорения  лежит на прямой, параллельной движению ползуна (в нашем случае параллельно (ОВ)).Строим в общем виде план ускорений для положения механизма, представленного на рис.2.2 (см. рис. 2.6).
лежит на прямой, параллельной движению ползуна (в нашем случае параллельно (ОВ)).Строим в общем виде план ускорений для положения механизма, представленного на рис.2.2 (см. рис. 2.6).
Порядок построения плана ускорений следующий: от полюса  строим ускорение точки А. Затем из конца вектора
строим ускорение точки А. Затем из конца вектора  проводим отрезок
проводим отрезок  , соответствующий вектору нормального ускорения
, соответствующий вектору нормального ускорения  . Через точку п проводим луч, перпендикулярный
. Через точку п проводим луч, перпендикулярный  . С другой стороны, из полюса
. С другой стороны, из полюса  проводим луч, параллельный ходу движения ползуна В, соответствующий вектору ускорения
проводим луч, параллельный ходу движения ползуна В, соответствующий вектору ускорения  . Точка пересечения лучей даст нам ускорение точки В – b.
. Точка пересечения лучей даст нам ускорение точки В – b.

Рис. 2.6. План ускорений механизма
Для определения численного значения ускорения точки В, воспользуемся формулой:
 , (2.16)
, (2.16)
где 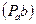 – расстояние на плане ускорений от полюса
– расстояние на плане ускорений от полюса  до точки b (мм).
до точки b (мм).
Угловое ускорение движения шатуна 2 определяем по формуле:
 , (2.17)
, (2.17)
где  – величина отрезка, взятого из плана скоростей (мм).
– величина отрезка, взятого из плана скоростей (мм).
2.5. Теорема подобия для плана ускорений
Теорема. Отрезки прямых линий, соединяющие концы векторов абсолютных ускорений точек на плане ускорений, и отрезки прямых линий, соединяющие одноименные точки на плане механизма, образуют подобные и сходственно расположенные фигуры.
Рассмотрим применение теоремы подобия для плана ускорений на примере механизма, изображенного на рис. 2.7 а.
Построим в общем виде план ускорений для этого механизма.
1. Определим ускорение точки А кривошипа. В общем случае  , где
, где  – нормальное ускорение;
– нормальное ускорение;  – тангенциальное ускорение. Численно
– тангенциальное ускорение. Численно  ;
;  , поскольку по условию задачи кривошип вращается равномерно. Таким образом, полное ускорение точки А равно ее нормальному ускорению:
, поскольку по условию задачи кривошип вращается равномерно. Таким образом, полное ускорение точки А равно ее нормальному ускорению: 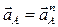 .
.
Вектор  направлен вдоль звена ОА от точки А к точке О (см. рис. 2.7 а).
направлен вдоль звена ОА от точки А к точке О (см. рис. 2.7 а).

Рис. 2.7
2. Определим ускорение точки В шатуна 2. На основании теоремы об ускорениях точек тела, совершающего плоскопараллельное движение, составим векторное равенство:  , где
, где  – ускорение точки В относительно точки А во вращательном движении шатуна 2 вокруг А; так как это движение неравномерное, то
– ускорение точки В относительно точки А во вращательном движении шатуна 2 вокруг А; так как это движение неравномерное, то  , следовательно,
, следовательно, 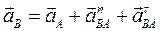 , где
, где  – соответственно нормальное и тангенциальное ускорения точки В в этом движении.
– соответственно нормальное и тангенциальное ускорения точки В в этом движении.
Вектор 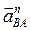 направлен вдоль отрезка АВ от точки В к точке А (см. рис. 2.7 а); вектор
направлен вдоль отрезка АВ от точки В к точке А (см. рис. 2.7 а); вектор  перпендикулярен отрезку ВА; точка В одновременно принадлежит звену 3, совершающему возвратно-поступательное движение вдоль оси Ох; следовательно, вектор
перпендикулярен отрезку ВА; точка В одновременно принадлежит звену 3, совершающему возвратно-поступательное движение вдоль оси Ох; следовательно, вектор 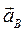 параллелен оси Ох. Численно
параллелен оси Ох. Численно 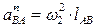 .
.
3. Зададимся длиной отрезка  и вычислим длину вектора, изображающего на плане ускорений
и вычислим длину вектора, изображающего на плане ускорений  :
:  .
.
4. На основании равенства  выполним построения (рис. 2.7 б):
выполним построения (рис. 2.7 б):
– из точки  проведем луч, параллельный кривошипу ОА, в направлении вектора
проведем луч, параллельный кривошипу ОА, в направлении вектора  (см. рис. 2.7 а) и отложим на нем отрезок
(см. рис. 2.7 а) и отложим на нем отрезок  ;
;
– из точки а проведем луч, параллельный отрезку АВ шатуна 2, в направлении вектора 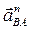 (см. рис. 2.7 а) и отложим на нем отрезок а п;
(см. рис. 2.7 а) и отложим на нем отрезок а п;
– через точку п проведем прямую, перпендикулярную АВ, а через точку  – прямую, параллельную оси Ох; их пересечение дает точку b. Вектор
– прямую, параллельную оси Ох; их пересечение дает точку b. Вектор 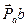 – ускорение точки В в масштабе
– ускорение точки В в масштабе  ;
;
– соединим на плане ускорений точку b с точкой а.
5. Определим ускорение точки С. Применим теорему подобия для плана ускорений:
– для построения на плане ускорений  , подобного
, подобного  , на плане механизма составим две пропорции
, на плане механизма составим две пропорции
 и
и  ,
,
откуда получим
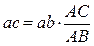 и
и  , (2.18)
, (2.18)
где  – длина отрезка на плане ускорений, мм;
– длина отрезка на плане ускорений, мм;
АВ, АС, ВС – длины отрезков на плане механизма, мм, которые могут быть получены измерением на плане механизма или взяты из условия задачи;
– используя результаты вычислений по формулам (2.18), выполним построения. Применим метод засечек: из точки а плана ускорений проведем дугу окружности раствором циркуля, равным ас. Из точки b проведем дугу окружности раствором циркуля, равным bc. Пересечение этих дуг дает точку с. При этом возможно два положения точки с, но верным является только одно из них. Правильность построений определяется условием сходственного расположения треугольников на плане ускорений и на плане положений механизма: если обходить вершины сторон треугольника АВС по ходу часовой стрелки, то получим последовательность их расположения А, В, С. Значит и при обходе вершин треугольника abc на плане ускорений по ходу часовой стрелки мы должны получить ту же последовательность их расположения – а, b, с. Это условие выполняется только при расположении точки с правее отрезка аb (см. рис. 2.7 б).
Соединим точку с с полюсом  . Вектор
. Вектор  – ускорение точки С в масштабе
– ускорение точки С в масштабе  .
.
Пример №4. Для заданного механизма (рис. 2.5 а) построить план ускорений и определить ускорения всех точек, а также угловые ускорения всех звеньев механизма. Исходные данные взять из примера №3.
Дано:  ,
, 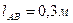 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Построить план ускорений механизма и определить:  ,
,  ,
,  ,
,  ,
, 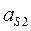 ,
,  .
.
Решение:
Ускорение точки А определяем по формуле (2.11):
 .
.
На плане ускорений отмечаем полюс  и строим отрезок
и строим отрезок  в направлении вектора
в направлении вектора  (рис. 2.8 а). Тогда масштабный коэффициент ускорения по формуле (2.12) будет равен:
(рис. 2.8 а). Тогда масштабный коэффициент ускорения по формуле (2.12) будет равен:
 .
.
По теореме о сложении ускорений при плоскопараллельном движении ускорение точки B равно  . Нормальную составляющую ускорения
. Нормальную составляющую ускорения  определим по формуле (2.14):
определим по формуле (2.14):
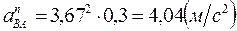 .
.
Отрезок на плане ускорений, соответствующий данному вектору нормального ускорения по формуле (2.15) будет равен:
 .
.
Из точки а на плане ускорений проводим луч, параллельный АВ, в направлении вектора 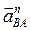 (рис. 2.8 а) и отложим на нем отрезок
(рис. 2.8 а) и отложим на нем отрезок  . Через точку п проведем прямую, перпендикулярную АВ (это линия действия вектора
. Через точку п проведем прямую, перпендикулярную АВ (это линия действия вектора 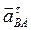 ), а из полюса
), а из полюса  прямую, параллельную ОВ – соответствующую направлению вектора
прямую, параллельную ОВ – соответствующую направлению вектора  . Их пересечение дает точку b (рис. 2.8 б).
. Их пересечение дает точку b (рис. 2.8 б).
Для определения численного значения ускорения точки В, воспользуемся формулой (2.16):
 .
.

Рис. 2.8
Угловое ускорение движения шатуна 2 определяем по формуле (2.17):
 .
.
Найдем ускорение остальных точек. Поскольку все точки звеньев совершают плоскопараллельное движение, то воспользуемся теоремой подобия для плана ускорений. Рассмотрим точку S2. Она принадлежит звену 2 и делит шатун АВ посередине. На плане ускорений точка s2 также будет делить отрезок аb пополам. Расстояние от полюса  до s2 и будет определять ускорение точки S2.
до s2 и будет определять ускорение точки S2.
Точка С тоже принадлежит звену 2 и расположена на расстоянии  . На плане ускорений она так же будет отстоять от точка а на расстоянии
. На плане ускорений она так же будет отстоять от точка а на расстоянии  . Соединяем полюс и точку с – этот и есть вектор скорости точки С.
. Соединяем полюс и точку с – этот и есть вектор скорости точки С.
Рассмотрим точку D. Она принадлежит звену 1.
Порядок определения ускорения точки D аналогичен точке С.
План ускорений построен.
После определения направлений ускорений точек на плане ускорений, определим численное значение ускорений точек аналогично определению численного значения ускорения точки В:
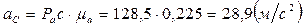 ,
,
 ,
,
 .
.
3. КИНЕТОСТАТИКА ПЛОСКОГО РЫЧАЖНОГО МЕХАНИЗМА
ГО КЛАССА
Основной задачей кинетостатического (силового) анализа механизмов является определение реакций в кинематических парах. Значение этих сил необходимо при расчете звеньев механизма на прочность, жесткость, виброустойчивость, износостойкость, при расчете подшипников на долговечность и проведении других подобных расчетов, выполняемых при проектировании механизмов.
Если свободному перемещению данного тела в пространстве не препятствуют другие тела, оно называется свободным. Если другие тела путем непосредственного контакта с данным телом мешают ему свободно перемещаться в пространстве, оно называется несвободным, а эти другие тела называются связями по отношению к данному телу.
Силы, с которыми связи действуют на данное тело, называются реакциями связей (пассивными силами). Если сила не является реакцией связи, то она является активной или задаваемой. Иначе – активными называются силы, появление которых не связано с непосредственным контактом или соприкосновением тел (например, силы гравитационного, электромагнитного взаимодействия, другие силы, физическая природа возникновения которых может быть неизвестна, но они не являются реакциями связей).
Принцип освобождаемости от связей. Любое несвободное тело можно условно считать свободным, если действие наложенных на него связей заменить реакциями этих связей.
Все силы, действующие на данное тело (систему тел), могут быть разделены на внешние и внутренние. Внешние – это силы  , действующие на данное тело или его точки со стороны других тел. Внутренние – это силы
, действующие на данное тело или его точки со стороны других тел. Внутренние – это силы  взаимодействия между точками или частями данного тела (системы тел). Все внутренние силы абсолютно твердого тела образуют уравновешенную систему сил. Реакции внешних связей для данного тела всегда являются внешними силами.
взаимодействия между точками или частями данного тела (системы тел). Все внутренние силы абсолютно твердого тела образуют уравновешенную систему сил. Реакции внешних связей для данного тела всегда являются внешними силами.
Деление сил на внешние и внутренние является условным. Все зависит от того, что выбрано за объект исследования, что принято за данную или рассматриваемую механическую систему. Например, объект исследования – двигатель внутреннего сгорания. Давление поршня на кривошип и давление кривошипа на поршень – внутренние силы. Те же силы будут внешними, если объект исследования – отдельно рассматриваемый поршень или кривошип.
Дополнительная задача динамического анализа механизмов состоит в определении уравновешивающей силы или уравновешивающего момента, приложенных к кривошипу. Эти силовые факторы являются функциями положения кривошипа и в данный момент обеспечивают его состояние покоя или равномерного вращательного движения
Кинетостатический расчет механизмов ведется по структурным группам, так как они обладают нулевой подвижностью и, следовательно, являются статически определимыми системами. Кинетостатический расчет начинается с расчета структурной группы, в которую входит самое удаленное ведомое звено механизма, и завершается расчетом ведущего звена – кривошипа.
При выполнении кинетостатического расчета механизма должен быть задан закон движения ведущего звена и проведен полный кинематический анализ. Кроме того, должны быть заданы все внешние силы, действующие на механизм, например, силы «полезного» (производственного) сопротивления. К данным силам также относятся силы тяжести звеньев, которые определяются формулой:
 , (3.1)
, (3.1)
где  – масса i -го звена, (кг);
– масса i -го звена, (кг);
 – ускорение свободного падения,
– ускорение свободного падения,  (м/с2).
(м/с2).
Кинетостатический расчет механизмов основан на использовании принципа Даламбера.
Участок 1.
Границы участка 


Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!