Способ плоско параллельного перемещения

При использовании способа вращения фигур иногда происходит наложение изображений. Этого можно избежать, применяя способ плоскопараллельного перемещения. Этот способ относится к способам третей группы.

Сущность этого способа заключается в том, что все точки геометрической фигуры перемещаются в плоскостях, параллельных одной из плоскостей проекций.

Следовательно, точки движутся в плоскостях уровня, и одна из проекций геометрической фигуры перемещается без изменения формы и размеров, а на другой проекции траектории движения точек параллельны оси 0 Х.

Рассмотрим преобразование отрезка АВ прямой общего положения в проецирующую прямую (рис. 89). Первоначально преобразуем прямую АВ во фронталь, переместив проекцию А ₁ В ₁ без изменения размеров параллельно оси 0 Х (в произвольном месте). Точки прямой АВ перемещаются параллельно плоскости π ₁. На фронтальной проекции траектории точек параллельны оси 0 Х. Новые фронтальные проекции отрезка А В определяются на пересечении линий связи от А В с траекториями движения точек.

 

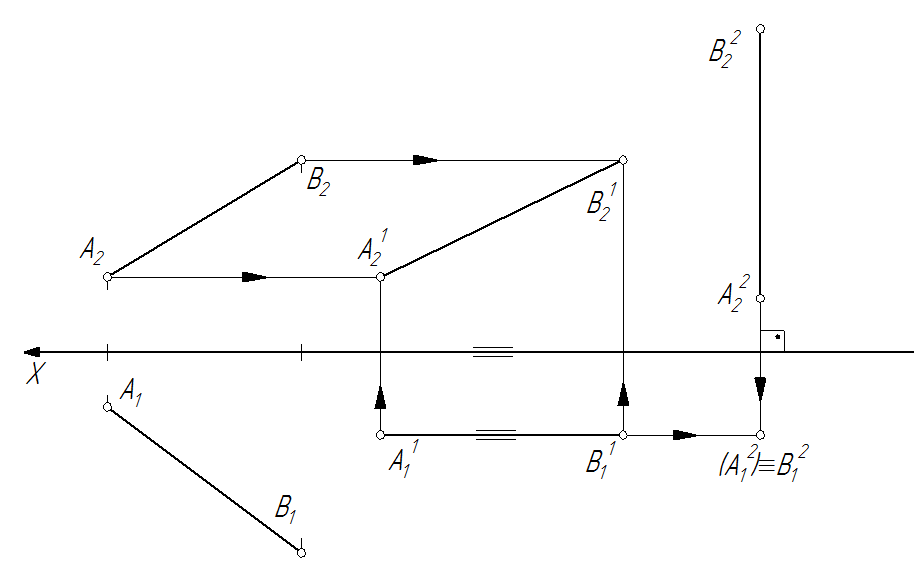
Рис. 89

Проекция А В является натуральной величиной АВ, так как первым перемещением прямая преобразована во фронталь (характерный признак – А В ∥0 Х).

Второе перемещение выполняется параллельно плоскости π₂. Фронтальная проекция перемещается без изменений размеров перпендикулярно оси 0 Х (А В ⊥0 Х). На горизонтальной проекции точки движутся параллельно оси 0 Х, и отрезок АВ преобразуется в горизонтально проецирующую прямую.

 

10.3. Определение натуральных величин
геометрических объектов

Определение натуральных величин геометрических объектов базируется на использовании четырех основных задач. К таким параметрам геометрических объектов относятся 15 основных параметров.

1. Определение натуральной величины отрезка. (Задача № 1).

2. Расстояние между двумя точками. Между точками проводится отрезок и решается задача № 1. Натуральная величина отрезка есть искомая величина.

3. Определение угла наклона прямой к плоскости проекций. Решается задача № 1 и используются свойства прямых уровней.

4. Расстояние от точи до прямой. Прямая переводится в проецирующие положение (задача № 2). Расстояние от проекции точки до вырожденной проекции прямой является искомой величиной.

5. Расстояние между скрещивающимися прямыми. Одна из прямых переводится в проецирующие положение (задача №2). Перпендикуляр от вырожденной проекции прямой до проекции другой прямой является искомой величиной.

6. Расстояние между параллельными прямыми. Одна из прямых переводится в проецирующие положение (задача № 2). Расстояние между вырожденными проекциями прямых является искомой величиной.

7. Натуральная величина плоской фигуры. Плоская фигура заключается в плоскость. Затем эта плоскость переводится в положение плоскости уровня (задача № 4). Натуральная величина плоской фигуры определяется по свойству плоскости уровня.

8. Угол между пересекающимися прямыми. Прямые заключаются в плоскость и плоскость переводится в положение уровня (задача № 4). Угол пересечения натуральных величин прямых является искомой величиной.

9. Угол между скрещивающимися прямыми. Используя параллельный перенос одной из прямых, прямые доводят до положения пересечения прямых и задачу решают, как определения угла между пересекающимися прямыми.

10. Угол наклона плоскости к плоскости проекций. Плоскость переводится в проецирующие положение (задача № 3). Угол наклона вырожденной проекции плоскости к оси является искомой величиной.

11. Расстояние от точки до плоскости. Плоскость переводится в проецирующие положение (задача № 3). Перпендикуляр от проекции точки до вырожденной проекции плоскости является искомой величиной.

12. Расстояние от прямой до плоскости, которой она параллельна. Плоскость переводится в проецирующие положение (задача № 3). Перпендикуляр между проекциями прямой и вырожденной проекцией плоскости является искомой величиной.

13. Расстояние между параллельными плоскостями. Одна из плоскостей переводится в проецирующие положение (задача №3). Перпендикуляр между вырожденными проекциями плоскостей является искомой величиной.

14. Определение двугранного угла. Линия пересечения плоскостей переводится в проецирующие положение (задача №2). Угол между вырожденными проекциями плоскостей является искомой величиной.

15. Определение угла наклона прямой к плоскости. Вначале плоскость переводится в плоскость уровня (задача № 4), а затем находится натуральная величина прямой (задача № 1). Угол между натуральной величиной прямой и вырожденной проекцией плоскости является искомой величиной.

 

Примечание. Если преобразование производится применительно к какому-то одному геометрическому образу, то оно относится ко всему изображению в целом.

10.4. Контрольные вопросы

1. Как определяется натуральная величина отрезка способом вращения вокруг проецирующей прямой?

2. Как получить проецирующею прямую способом вращения вокруг проецирующей прямой?

3. Как получить проецирующею плоскость способом вращения вокруг проецирующей прямой?

4. Как получить плоскость уровня способом вращения вокруг проецирующей прямой?

5. В чем заключается сущность способа плоско параллельного перемещения и в каких случаях он применяется?

6. Перечислите основные геометрические характеристики, определяемые способами преобразования чертежа.

 

 

Лекция 11. ПОВЕРХНОСТИ

11.1. Многогранники.

11.2. Задание многогранника на эпюре Монжа.

11.3. Классификация поверхностей.

11.3. Задание поверхностей вращения на эпюре Монжа.

11.4. Контрольные вопросы.

Многогранники

Отдельным классом поверхностей выделены многогранники. Многогранной поверхностью называется поверхность, образованная частями пересекающихся плоскостей. Если плоскости при этом замыкают пространство со всех сторон, то они образуют многогранник. Говоря другими словами многогранниками это тела, ограниченные плоскими п -угольниками называемыми гранями.

Из всего многообразия многогранников наибольший практический интерес представляют пирамиды, призмы и правильные многоугольники.

Пирамида – это многогранник, одна грань которого многоугольник, а остальные грани треугольники с общей вершиной – рис. 90а.

 

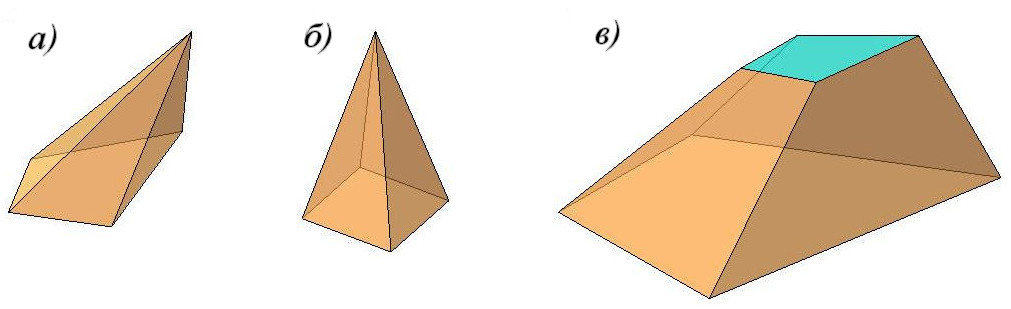
Рис. 90

Пирамиду называют правильной, если основанием ее является правильный многоугольник и высота пирамиды (перпендикуляр, опущенный из вершины на основание) проходит через центр этого многоугольника – рис. 90б.

Пирамида называется усеченной, если вершина ее отсекается плоскостью, пересекающей все ребра, исходящие из этой вершины – рис. 90в.

Призмой называют многогранник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани – параллелограммы – рис. 91а.

Призму называют прямой, если ребра ее перпендикулярны плоскости основания – рис. 91б. Если основанием призмы является прямоугольник, призму называют параллелепипедом – рис. 91в.

Правильные многоугольники. Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильным. Углы при вершинах такого многогранника равны между собой. Более двух тысяч летназад древнегреческий философ Платон описал все 5 видов правильных многогранников. Поэтому эти многогранники называют телами Платона.

Рис. 91

Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (рис. 92а). Это и правильная треугольная пирамида. Каждая из четырех граней тетраэдра может быть выбрана в качестве её основания. Перпендикуляр, опущенный из любой вершины тетраэдра на противолежащую грань, проходит через ее центр.

Октаэдр – правильный восьмигранник (рис. 92б). Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре у каждой вершины. Каждая из диагональных плоскостей делит октаэдр на две пирамиды с основаниями в виде квадрата.

Гексаэдр – правильный шестигранник (рис. 92в). Это куб, состоящий из шести равных квадратов.

Додекаэдр – правильный двенадцатигранник состоит из 12 правильных и равных пятиугольников, соединенных по три около каждой вершины. Два противолежащих пятиугольника можно принять за основания додекаэдра.

Икосаэдр – состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины.

 

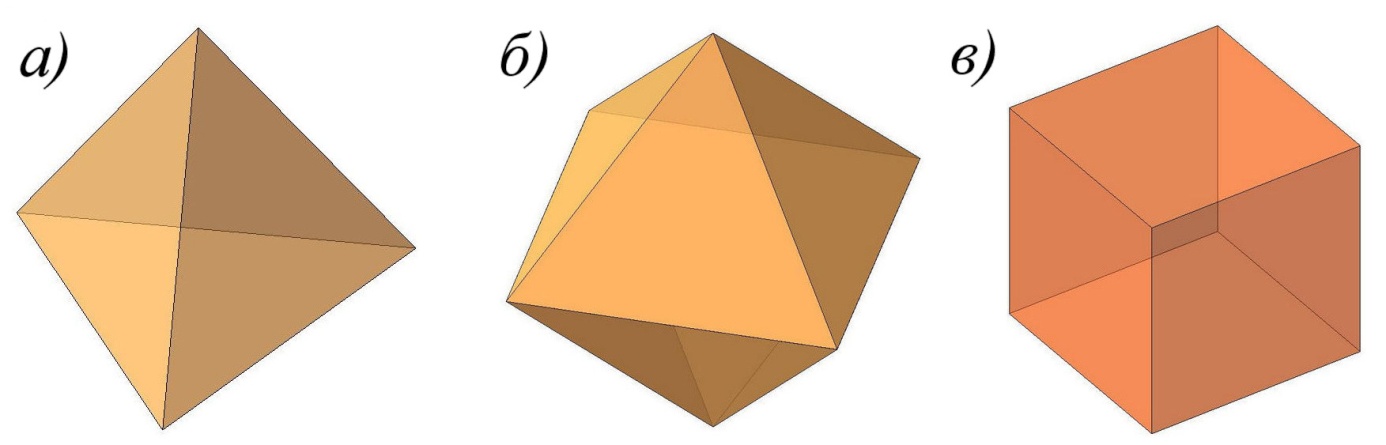
Рис. 92

Леонард Эйлер (1707-1783 гг.) открыл и доказал знаменитую теорему, связывающую числа граней (Г),вершин (В) и ребер (Р) любого выпуклого многогранника: Г + В – Р = 2. Здесь число 2 называют числом Эйлера.

Задание многогранников на эпюре Монжа

Как видно из рис. 93, каждый многогранник содержит грани, ребра и вершины. Их совокупность называется сеткой. На эпюре многогранники изображаются проекциями своей сетки – рис. 94. Каждая вершина имеет своё обозначение. Ребра многогранников есть линии пересечения смежных граней. Каждая грань – это часть плоскости, ограниченной ребрами и сторонами основания многогранника.

Рассмотрим, в каком случае точка пространства будет принадлежать многограннику.

Рис. 93

Понятно, что точка пространства может принадлежать: вершине многогранника, его ребру или грани многогранника.

В первом и втором варианте проблем изображения точки на чертеже многограннике нет.

Если же точка принадлежит грани многогранника, т.е. плоскости, надо пользоваться информацией: точка лежит в плоскости, если она лежит на прямой этой плоскости.

Условимся записывать обозначение точки, лежащей на невидимой для наблюдателя грани, в скобках, например, (E ₂).

На рис. 94а задана проекция (E ₂), т.е. точка E располагается грани ADS четырёхгранной пирамиды, невидимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проводится прямая S- 1 в грани BCS через вершину S, на горизонтальной проекции которой и лежит E ₁.

На рис. 94б задана проекция F ₂, т.е. точка F располагается на грани BCS правильной четырёхгранной пирамиды, видимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проводится в грани BCS прямая, параллельная стороне AD основанияпирамиды. На горизонтальной проекции этой прямой и лежит F ₁.

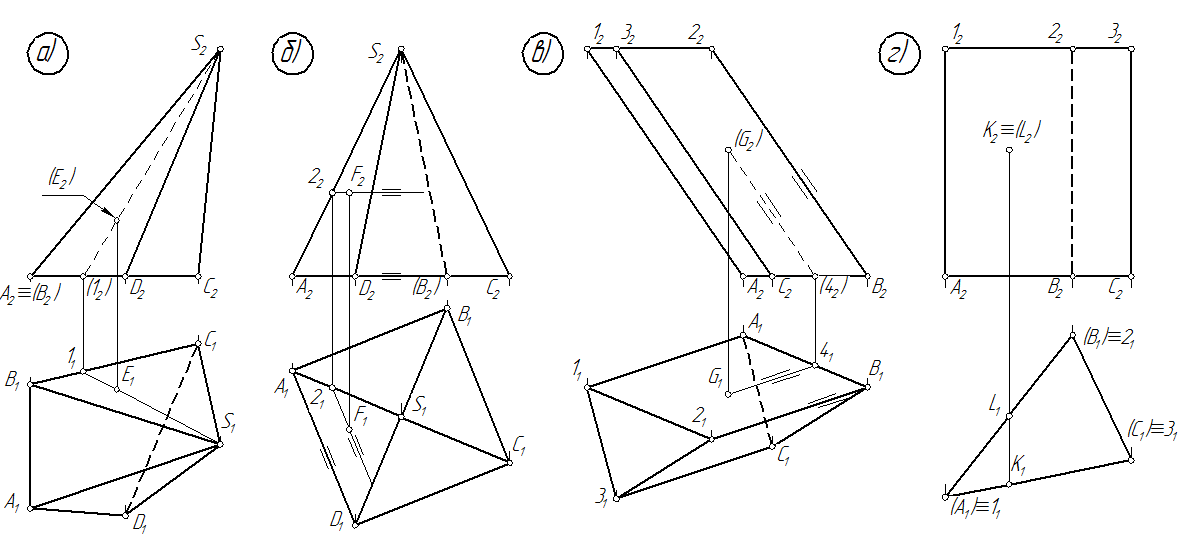
Рис. 94

На рис. 94в задана проекция (G ₂), т.е. точка G располагается на грани
1 - 2 -BA наклонной призмы, видимой относительно фронтальной плоскости проекции. Для нахождения горизонтальной проекции проведена в грани
1 - 2 -BA прямая, параллельная ребрам призмы. На горизонтальной проекции этой прямой и лежит G ₁.

У прямой призмы (рис. 94г) грани занимают горизонтально-проецирующее положение, поэтому горизонтальные проекции K ₁ и L ₁ определяются с помощью вертикальных линий связи на следах граней.

Классификация поверхностей

Для того, чтобы ориентироваться во всем многообразии поверхностей, в способах задания и изображения поверхностей, необходимо классифицировать поверхности по общим, наиболее характерным признакам. Практически каждая поверхность может быть образована несколькими способами. Однако наиболее целесообразным способом образования поверхностей является кинематический, основанный на определенных законах движения. Такой подход к рассмотрению поверхностей позволяет выполнить их классификацию и, что не менее важно, выбрать наиболее рациональную технологию их воссоздания в металле или в другом материале.

Рассмотрим аппарат получения поверхностей (рис. 95).

Введём обозначения:

– S – центр (точка относительно которой перемещается образующая);

– g – от слова genero (образую, порождаю);

– d – от слова dirigo (направляю).

Идея кинематического способа образования поверхностей состоит в том, что линия g,относительно центра S, в пространстве перемещается вдоль направляющей d и при движении образует поверхность. Линия может поступательно перемещаться, или вращается, или перемещается по винтовому закону, или, как по перилам, скользит по заданным линиям.

 

Рис. 95

Линия g называется в этом случае образующей, а множество ее положений в пространстве образует кривую поверхность Ф.

Линии d, по которым скользит образующая g, называются направляющими. Значит, образующие g и направляющие d обязательно пересекаются друг с другом. Очевидно, от формы образующей и характера её изменения зависит класс поверхности.

Если образующая g – прямая линия, то поверхность Ф называется линейчатой.

Если образующая g – кривая линия, то поверхность называется нелинейчатой.

Таким образом, выделено два класса поверхностей – линейчатые и нелинейчатые.

Из наиболее часто встречающихся в технике поверхностей выделены поверхности вращения.

Поверхностью вращения называется поверхность, образованная вращением образующей g вокруг оси вращения.

На рис. 96 изображены линейчатая поверхность вращения (конус), нелинейчатая поверхность вращения (глобоид) и многогранник (пирамида).

При вращении образующей, каждая ееточка описывает окружность с центром S на оси вращения. Эти окружности называются параллелями. Параллель с минимальным размером радиуса называется горлом, а с максимальным размером радиуса – экватором.

 

Рис. 96

Кривые, получающиеся в сечении тела вращения плоскостями, проходящими через ось, называются меридианами. Меридиан, параллельный фронтальной плоскости проекций, называется главным.

При вращении кривой 2-го порядка вокруг её оси образуется поверхность 2-го порядка:

· окружность вокруг диаметра – сфера,

· эллипс вокруг малой оси – сжатый эллипсоид вращения,

· эллипс вокруг большой оси – вытянутый эллипсоид вращения,

· парабола вокруг оси – параболоид вращения,

· гипербола вокруг мнимой оси – однополостный гиперболоид вращения,

· гипербола вокруг действительной оси – двуполостный гиперболоид вращения.

Если вращать вокруг оси прямолинейную образующую (прямую), то возможны 3 вида поверхностей:

· если g пересекает ось вращения – коническая поверхность вращения,

· если g параллельна оси вращения – цилиндрическая поверхность вращения,

· если g скрещивается с осью вращения – однополостный гиперболоид вращения.

Задание поверхностей вращения на эпюре Монжа

Поверхность на эпюре задается очерком. Очерк поверхности – это линия, разграничивающая проекцию фигуры от остального пространства чертежа. Для построения очерка необходимо построить крайние граничные очерковые образующие. Очерковые образующие лежат в плоскости, параллельной плоскости проекций.

На рис. 97 приведены примеры изображения некоторых тал вращения на эпюре Монжа: прямой круговой конус (рис. 97а); наклонный круговой конус (рис. 97б); прямой круговой цилиндр (рис. 97в); наклонный круговой цилиндр (рис. 97г).

Рис. 87

Если очерки для тела вращения (кроме сферы) называются в зависимости от плоскости проекций на которую оно спроецировано (горизонтальная, фронтальная и профильная), то для сферы (рис. 98) эти очерки носят специфические названия (по аналогии с глобусом):

– очерк на π ₂ – главный (нулевой) меридиан;

– очерк на π ₁ – экватор;

– очерк на π ₃ – профильный меридиан.

 

Рис. 98

Для построения точек на поверхностях используются образующие, проходящие через эти точки.

На рис. 97а задана проекция точки (А ₂), т.е. точка А располагается на невидимой стороне прямого кругового конуса относительно фронтальной плоскости проекций. Для нахождения горизонтальной проекции проводится образующая S- 1, на горизонтальной проекции которой и лежит А ₁.

На рис. 97б задана проекция В ₁ точки В, лежащей на видимой стороне наклонного кругового конуса относительно горизонтальной плоскости проекций. Для нахождения фронтальной проекции проводится образующая S- 2, на фронтальной проекции которой и лежит В ₂.

У прямого кругового цилиндра (рис. 97в) боковая поверхность занимает горизонтально-проецирующее положение, поэтому горизонтальные проекции С ₁ и D ₁ определяются с помощью вертикальных линий связи на следе боковой поверхности.

На рис. 97г заданы проекции Е ₂ и (F ₂) точек Е и F расположенных соответственно на видимой и невидимой сторонах наклонного цилиндра относительно фронтальной плоскости проекций. Для нахождения горизонтальных проекций проводятся образующие, параллельные очерковым боковой поверхности на которых находятся горизонтальные проекции этих точек Е ₁ и F ₁.

Для нахождения точек на поверхности сферы используют дополнительные широты и удаления от оси вращения.

На рис. 99 задана проекция G ₂ точки G, лежащей ниже экватора на видимой стороне сферы относительно фронтальной плоскости проекций. Для нахождения горизонтальной проекции: вначале строится дополнительная широта, проходящая через заданную точку, а затем по инварианту принадлежности определяется горизонтальная проекция точки (G ₁).

Рис. 99

Следует отметить, что проекция точки на горизонтальной плоскости проекций не видима, т.к. точка G располагается ниже экватора.

Профильная проекция точки G ₃ определяется по горизонтальной линии связи и удалению от оси вращения (см. рис. 99). Проекция G ₃ видима потому, что фронтальная проекция точки G ₂ находится правей фронтальной проекции профильного меридиана.

11.5. Контрольные вопросы

1. Как образуются многогранники?

2. Перечислите основные элементы многогранников.

3. Перечислите основные виды многогранников.

4. Как изображаются многогранники на эпюре?

5. Как определяются точки на поверхности многогранника?

6. Перечислите элементы аппарата получения поверхностей.

7. Как образуются поверхности вращения?

8. Как изображаются поверхности на эпюру?

9. Как называются очерки сферы на эпюре?

10. Как определяются точки и линии на поверхностях?

 

Лекция 12. ПОВЕРХНОСТИ

12.1. Виды сечений.

12.2. Построение сечения проецирующей плоскостью.

12.3. Пересечение прямой с поверхностью.

12.4. Контрольные вопросы.

Виды сечений

Вид сечения поверхности зависит от типа поверхности и положения секущей плоскости относительно поверхности.

Независимо от расположения секущей плоскости, сечением многогранника будет многоугольник, вершинами которого будет является точки пересечения секущей плоскости с ребрами многогранника (рис. 100).

Рис. 100

Сечением цилиндра является круг если секущая плоскость перпендикулярна оси вращения (рис. 101а), овал (элепс) если секущая плоскость не перпендикулярна и не параллельна оси вращения (рис. 101б) или прямоугольник если секущая плоскость параллельна оси вращения (рис. 101в).

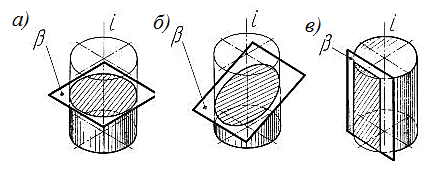
Рис. 101

Сечением сферы всегда является круг (рис. 102).

Рис. 102

Рассмотрим более подробней сечение конуса. Поверхность конуса вращения определяется уравнением 2-го порядка значит, и сечением конуса могут быть кривые 2-го порядка, т.е. окружность, эллипс, парабола или гипербола.

В начертательной геометрии тип кривой 2-го порядка может быть определен следующим образом.

Если секущая плоскость параллельна двум образующим конуса, то сечением будет гипербола. Обе ветви гиперболы можно получить, если конус будет иметь две полы. На рис. 103 плоскость А-А проходит параллельно двум образующим конуса (S- 1 и S- 2) и поэтому пересекает конус по гиперболе. Слева изображена истинная величина сечения А-А и 3-мерное изображение конуса с сечением А-А.

Если секущая плоскость параллельна одной образующей конуса, то сечением будет парабола. На рис 103 плоскость Б-Б проходит параллельно правой очерковой образующей S- 3 конуса, поэтому сечением является парабола, истинная величина которой показана справа с сопровождающей надписью Б-Б. Ещё правее и ниже дано 3-мерное изображение конуса, усеченного плоскостью Б-Б.

Если секущая плоскость пересекает все образующие, то сечением будет эллипс. Плоскость В-В пересекает все образующие верхней полы конуса. Значит, сечением будет являться эллипс. Истинная величина сечения размещена справа с надписью В-В. Ещё правее и чуть выше показана 3-мерная модель конуса, усечённого плоскостью В-В.

Если секущая плоскость перпендикулярна к оси вращения конуса, то сечением будет окружность. На рис. 103 основания конуса перпендикулярны оси конуса OS и поэтому являются окружностями, горизонтальные проекции которых совпадают.

Если секущая плоскость проходит через вершину S конуса и пересекает его, то понятно, что в сечении будут треугольники (образующие конуса и линия сечения основания). Если секущая плоскость проходит через S и не пересекает образующие, сечением будет точка S. На рис. 29 сечения от плоскости b А-А, Б-Б, В-В и построены в натуральную величину и размещены в проекционной связи с секущей плоскостью.

Рис. 29

На правой части рис. 103 изображены фронтальная и горизонтальная проекции того же конуса. Но здесь показаны приёмы получения в сечении гиперболы. Для этого через фронтальную проекцию S ₂ вершины S под любым углом проводим проекции образующих S-1 и S-2 конуса, лежащих во фронтально проецирующей плоскости. Затем параллельно плоскости этих образующих проводим фронтальный след a₂ плоскости a сечения. Строим горизонтальную проекцию гиперболы, опорными точками которой являются точки А, С и вершина В. Понятно, что эта проекция гиперболы не определяет истинной величины сечения.

Ещё один вариант построения сечения в виде гиперболы получается, если секущая плоскость b будет параллельна фронтальной плоскости проекций, так как в этом случае плоскость b параллельна двум образующим – S- 3, S- 4. Фронтальная проекция гиперболы (D и F – опорные точки сечения, а E – вершина гиперболы) есть истинная величина сечения.