Стационарные функции, характеристики которых полученные по одной реализации, являются представительными для всех реализаций и для всей функции в целом, называются эргодическими.
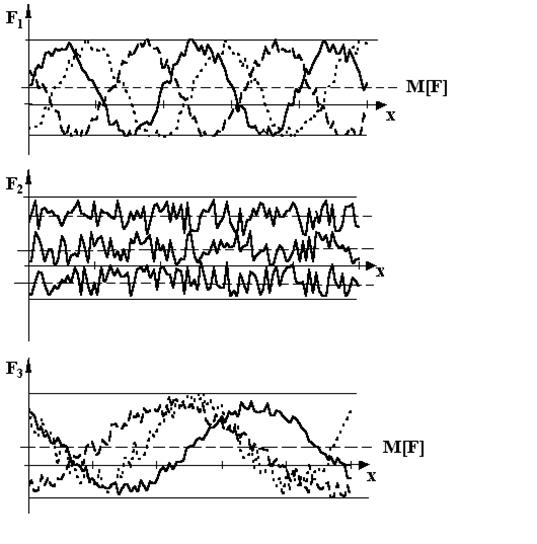
Рис. 1.2
На рис. 1.2. приведены стационарные случайные функции, кроме того F1 и F3 являются также и эргодическими.
Для эргодических случайных функций оценки статистических характеристик могут вычисляться по более простым формулам по одной реализации.
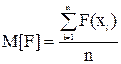 (1.3)
(1.3)
 (1.4)
(1.4)
где: n- число значений случайной функции в одной реализации.
Математическое ожидание определяет среднюю линию, а дисперсия - полосу, в которой осуществляются реализации случайной функции. Однако, поведение функции внутри полосы бывает совершенно различным.
Так, например, F1 и F2 имеют примерно одинаковые M[F] и D[F], однако, колебания функций различны.
Характеристикой изменчивости какой-либо реализации функции вдоль оси абсцисс может служить величина зависимости между соседними значениями функции. Эта зависимость оценивается автокорреляционной функцией (АКФ).
Для функций с дискретным аргументом (т.е. когда измерения проведены по регулярной сети). Автоковариационная функция вычисляется по формуле:
 (1.5)
(1.5)
автокорреляционная функция:
AKФF(θ) = rF( (1.6)
(1.6)
здесь:  - величина сдвига реализации случайной функции, равная 1,2,..m пикетам.
- величина сдвига реализации случайной функции, равная 1,2,..m пикетам.
Рассмотрим пример вычисления автокорреляционной функции.
Пусть дана реализация случайной функции. Рис.1.3(a).
Рис. 1.3(а)
| xi
|
|
|
|
|
|
|
|
|
|
|
| F(xi)
|
| -4
| 6,5
|
| 3,7
| -8,5
| 2,1
| 2,5
| -2,0
| -4,8
|
Математическое ожидание M[F] =0.
Требуется построить автокорреляционную функцию.
1. Пусть  =0
=0
| xi
|
|
|
|
|
|
|
|
|
|
|
| F(xi)
|
| -4
| 6,5
|
| 3,7
| -8,5
| 2,1
| 2,5
| -2,0
| -4,8
|
| F(xi)
|
| -4
| 6,5
|
| 3,7
| -8,5
| 2,1
| 2,5
| -2,0
| -4,8
|
KF(0) = 30,2; rF(0) =1
Значение автоковариационной функции для  =0 соответствует
=0 соответствует
дисперсии D[F]=30,2.
Рис. 3.1.3(б)
2. Пусть  =1 KF1(1)=
=1 KF1(1)= 
| xi
|
|
|
|
|
|
|
|
|
|
|
| f(xi)
|
|
| -4
| 6,5
|
| 3,7
| 8,5
| 2,1
| 2,5
| -2,0
|
| f(xi+1)
|
| -4
| 6,5
|
| 3,7
| 8,5
| 2,1
| 2,5
| -2,0
| -4,8
|
KF(1)=6,6 rF(1)=0,219
3. Пусть  =2 KF2(2)=
=2 KF2(2)= 
| x1
|
|
|
|
|
|
|
|
|
| f(xi)
|
| -4
| 6,5
|
| 3,7
| 8,5
| 2,1
| 2,5
|
| f(xi+2)
| 6,5
|
| 3,7
| -8,5
| 2,1
| 2,5
| -2,0
| -4,8
|
KF(2)=-8,6 rF(2)= -0,285
4. Сдвигая функцию в дальнейшем на  =3,4,5,...m (Рис. 3.1.3(б)) получим последующие значения функций.
=3,4,5,...m (Рис. 3.1.3(б)) получим последующие значения функций.
KF(3)=-1,8 rF(3)=-0,06
KF(4)=10,0 rF(4)=0,33
KF(5)=-1,2 rF(5)=0,04
На рисунке 1.3(в) приведен график автокорреляционной функции для нашего примера.
Рис. 1.3(в)
Автокорреляционная функция симметрична относительно вертикальной оси. При  =0, rF(0)=1.
=0, rF(0)=1.
Для различных  автокорреляционная функция представляет собой коэффициенты корреляции двух случайных величин F(xi) и F(
автокорреляционная функция представляет собой коэффициенты корреляции двух случайных величин F(xi) и F( ). По автокорреляционной функции можно построить корреляционную матрицу.
). По автокорреляционной функции можно построить корреляционную матрицу.
CorF( (1.7)
(1.7)
здесь: 
Числовой характеристикой зависимости значений случайной функции вдоль профиля является радиус корреляции R, т.е. такое среднее расстояние, на котором сохраняется положительная корреляционная связь в структуре случайной функции. Для определения радиуса корреляции используют оценки значимости коэффициента корреляции при заданной ошибке 1 рода. В простейшем случае радиус корреляции (R) представляет собой расстояние от начала координат до пересечения rF с осью абсцисс. Удвоенный радиус корреляции 2R характеризует средний полупериод колебаний случайной функции. Если R<1 - исследуемая функция называется некоррелируемой.
Для некоррелированной случайной функции корреляционная матрица становится единичной, а ковариационная - скалярной.
По АКФ оцениваются корреляционные свойства геологических полей, аномалий, а также помех. Поскольку геофизическое поле представляет собой в общем случае сумму сигнала a(x) и помехи v(x) F(x)= a(x)+v(x) и при независимости аномалии и помехи АКФ можно представить в виде
 (3.1.8)
(3.1.8)
Последние две суммы в силу предположения равны нулю.
При слабом влиянии помехи на аномалию, т.е. при малой интенсивности помехи по сравнению с амплитудой аномалии, АКФ - является оценкой корреляционных свойств аномалий. При площадном моделировании, например при геологическом картировании по радиусу корреляции геологического поля по опорному профилю можно определить среднюю ширину аномалий, отражающих геологических подразделений
Lср.=2R
При отсутствии сигнала АКФ - представляет собой оценку корреляционных свойств помех. Погрешность оценки АКФ можно найти аналогично проверке значимости коэффициента корреляции по критерию Неймана-Пирсона.
Взаимно корреляционная функция (ВКФ) представляет собой оценку корреляционных свойств двух случайных полей F1 и F2.
В качестве исследуемых полей можно взять два различных геофизических или геохимических поля по одному профилю F1 и F2, и тогда ВКФ равна:
ВКФ =  (3.1.10)
(3.1.10)
Надежность вычисления ВКФ определяется аналогично АКФ.
2. Линейная фильтрация полей
Для решения одной из основных задач обработки геологических полей (собственно геологических, геофизических или геохимических полей) на начальной стадии их анализа наиболее широко применяются различные приемы фильтрации.
Предварительная оценка корреляционных или спектральных свойств полезных сигналов и помех позволяет обосновать применение того или иного фильтра, т.е. отфильтровать (сгладить) исходные геологические поля с целью выявления полезного сигнала и подавления помехи.
Выбор фильтра проводится в рамках сформулированной, определенной математической модели наблюдаемого поля. Наиболее широко используется аддитивная модель, в которой результаты измерения геологического поля F(x) представляют собой сумму полезного сигнала a(x) и осложняющей его помехи v(x)
F(x)=a(x)+v(x)
Под сигналом понимается закономерная часть случайного поля, которая содержит полезную информацию о геологическом объекте.
Помеха - случайная часть поля представляет собой возмущения, препятствующие выделению полезной информации.
Помеха может быть геологического происхождения (связанная с неоднородностями изучаемых геологических тел, влиянием перекрывающих насосов, вторичных геологических процессов и др.) и технического происхождения, связанная с погрешностями измерений, вариациями поля и т.д.
Понятия полезного сигнала и геологической помехи могут носить относительный характер. Так при детальном картировании, т.е. при выделении локальных аномалий от мелких геологических тел региональную составляющую, связанную с крупными геологическими подразделениями, можно считать помехой, и наоборот, при картировании более мелкого масштаба локальные аномалии могут выступать в роли помехи при выделении крупных геологических подразделений.
Относительный характер понятий сигнала и помехи иллюстрируется моделью
F(x)= aрег(x) + aлок(x) + vтех(x)
Аналогичная картина связана с влиянием вторичных процессов, например, мигматизацией. В этом случае при картировании стратиграфических сигналом, а аномалии от вторичных процессов - помехой и наоборот, при выяснении истории формирования геологического пространства аномалии авт(x), связанные со вторичными процессами, будут выступать в качестве полезного сигнала, а локальные аномалии от первичных пород - помехой.
F(x) = aстр(x) + авт(x) + v(x)
Поскольку любое наблюдаемое поле представляет собой суперпозицию различных аномалий и помех, основная задача при анализе геологических, геофизических или геохимических полей состоит в выделении аномалий, обусловленных изучаемыми геологическими объектами на фоне помех, а также в разделении поля на составляющие различной природы. После фильтрации аномалий осуществляется их выделение, площадное прослеживание и классификация, т.е. установление геологической породы выделенных и прослеженных по площади аномалий.
Учитывая изменение физических свойств горных пород и геометрических размеров, изучаемых геологических тел по простиранию наиболее обоснованной моделью геологического пространства, следует считать статистическую модель в виде случайного поля. Выбор той или иной модели исходного поля, а также методов анализа геологического поля определяется полнотой априорной информации, совершенством физико-геологической модели исследуемого геологического пространства.
Наличие достаточной априорной информации о свойствах геологического пространства и геолого-геофизических полей дает возможность применять оптимальные процедуры обработки для фильтрации и выделения полезных сигналов. Большое значение при этом имеют их коррелируемость вкрест и вдоль простирания геологических объектов, что способствует более успешному решению задачи выделения и прослеживания сигналов на фоне помех. Следовательно, при обработке геолого-геофизических и геохимических полей с целью выявления различных составляющих полезного сигнала важное место занимает фильтрация наблюдаемых полей в частности линейная фильтрация.
Простейшим способом фильтрации является усреднение по различным реализациям случайной функции, т.е. нахождение ее математического ожидания. Рис. 2.1.
 (2.1)
(2.1)
где: k - номер реализации, N- число реализации случайного поля.
Недостатком этого способа фильтрации является требование нескольких реализаций на одном и том же профиле, т.е. фактически нескольких контрольных маршрутов (см. Рис. 3.1.1).
Вычисление оценки математического ожидания стационарной случайной функции проводится по формуле:
 (2.2)
(2.2)
где: n - число пикетов на профиле.
Также можно рассматривать, как своего рода сглаживание, только по одной реализации.
Естественно возникает желание распространить эту идею и на нестационарные случайные функции. Это можно сделать, если случайная функция достаточно протяженна и подсчет среднего осуществляется на интервале, в пределах которого случайную функцию можно приближенно считать стационарной. За сглаженное значение функции в этом случае принимается среднее значение случайной функции внутри интервала L с центром в точке xj рис. 3.2.1. (Среднее значение  относится к середине интервала)
относится к середине интервала)

Перемещая интервал вдоль оси Х, каждый раз подсчитывая среднее значение внутри интервала получим отфильтрованное поле. Рассмотренный метод носит название скользящего среднего или скользящего окна.
В этом случае фильтрация случайной функции методом скользящего окна по одной ее реализации осуществляется по формуле
 (2.3)
(2.3)
где: L- ширина окна (нечетное число пикетов),
j- номер центрального пикета в окне,
i- номер пикета в пределах окна.
Чем больше L, тем лучше сглаживание, тем более плавной получится сглаженная функция, которой мы фактически оцениваем истинное математическое ожидание. Однако при слишком большом L сгладится и само математическое ожидание случайной функции. Следовательно, возникает задача определения длины окна.




Рис. 2.1
При решении этой задачи обычно исходят из характера корреляционных свойств случайной функции, о которых судят по величине
радиуса корреляции R. Длина фильтра не должна превышать 2R.
Проведем фильтрацию случайной функции приведенной в таблице и Рис. 2.2(а).
Рис 2.2(а)
Прежде всего, вычислим автокорреляционную функцию. Рис.2.2(б).
Рис. 2.2(б)
Рис 2.2(б)
Анализ автокорреляционной функции показывает, что в реализации случайной функции представлены два вида колебаний:
1) c полупериодом, равным 2R=9 пикетам;
2) коротко - периодические колебания, отражающие ошибки
наблюдений.
Эти коротко - периодические колебания, которые в данном случае являются помехой, необходимо отфильтровать. Поэтому ширину окна выбираем (L=7)<9 (нечетное число пикетов).
Отфильтрованное поле приведено на рис. 2.2(в).
Преобразование исходного поля линейным фильтром в общем виде описывается выражением
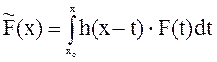 (2.4)
(2.4)
где: F(t) - исходное поле, h- весовая функция.
Это выражение, является интегралом Дюамеля или интегралом свертки.
Дискретным аналогом интеграла Дюамеля является выражение
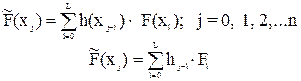 (2.5)
(2.5)
Заменяя (j-l) =i получим другую форму свертки
 (2.6)
(2.6)
или перенося вычисления в центр окна длиной L
 (2.7)
(2.7)
Рис.2.2(в)
Рассмотренный выше прием линейной фильтрации скользящее среднее, описываемый выражением (2.3) является частным случаем выражения (2.7), если в качестве весов принять hi=1/L.
Уравнение свертки (2.5) устанавливает связь между исходными и отфильтрованными полями через весовую функцию и при построении любых линейных фильтров является основным. Проблема фильтрации по существу и состоит в определении весовой функции, исходя из поставленной задачи, выбранной математической модели изучаемого поля и полноты априорной информации о полезном сигнале и помехи.













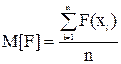 (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6) - величина сдвига реализации случайной функции, равная 1,2,..m пикетам.
- величина сдвига реализации случайной функции, равная 1,2,..m пикетам.




 автокорреляционная функция представляет собой коэффициенты корреляции двух случайных величин F(xi) и F(
автокорреляционная функция представляет собой коэффициенты корреляции двух случайных величин F(xi) и F( ). По автокорреляционной функции можно построить корреляционную матрицу.
). По автокорреляционной функции можно построить корреляционную матрицу. (1.7)
(1.7)
 (3.1.8)
(3.1.8) (3.1.10)
(3.1.10) (2.1)
(2.1) (2.2)
(2.2) относится к середине интервала)
относится к середине интервала)
 (2.3)
(2.3)






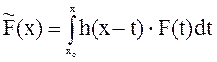 (2.4)
(2.4)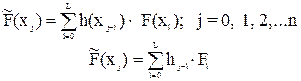 (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7)













