Чтобы достичь существенного улучшения эффективности необходимо разложить вычисления ДПФ на набор ДПФ меньшего порядка. Алгоритмы, в которых это разложение основано на разложении последовательности 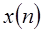 на меньшие подпоследовательности, называются алгоритмами с прореживанием по времени.
на меньшие подпоследовательности, называются алгоритмами с прореживанием по времени.
Рассмотрим частный случай  .
.  ,
,  . Разделим
. Разделим 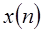 на четные и нечетные точки:
на четные и нечетные точки:  , или, заменяя индексы суммирования на
, или, заменяя индексы суммирования на  при четном n и
при четном n и  при нечетном, получим
при нечетном, получим  =
=  , т.к.
, т.к.  , то
, то
 = = 
| (1.54)
|
Каждая из сумм является N/2 точечным ДПФ. Первая сумма N/2 точечное ДПФ четных точек исходных последовательностей, а вторая – N/2 точечное ДПФ нечетных точек исходных последовательностей. Хотя индекс k простирается на N значений, k=0,1,…,N-1, каждая из сумм требует вычислений только для k от 0 до N/2-1, т.к. G(k) и H(k) периодичны по k с периодом N/2.
После того, как ДПФ, соответствующие двум суммам в (1.54), вычислены, они объединяются и дают N-точечное ДПФ 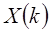 .
.
Рис. 1.4. Разложение 8-точечного ДПФ
Рис. 1.5.
Разложение 4-точечного ДПФ.
Рис. 1.6. 2-х точечное ДПФ.
Проведя разложение максимально возможное число раз, получим общее число комплексных умножений и сложений, равное  .
.
Вычисления с замещением
Направленный граф для полного разложения восьмиточечного ДПФ в алгоритме с прореживанием по времени изображен на Рис. 1.7. На каждой ступени вычислений происходит преобразование множества из N комплексных чисел в другое множество из N комплексных чисел. Этот процесс повторяется  раз, определяя в результате дискретное преобразование Фурье. Обозначим последовательность комплексных чисел, получающихся на m-ой ступени вычисления, через
раз, определяя в результате дискретное преобразование Фурье. Обозначим последовательность комплексных чисел, получающихся на m-ой ступени вычисления, через 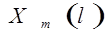 , где
, где 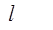 =
=  и m=1,2,…
и m=1,2,…  . Можно считать
. Можно считать  входным массивом, а
входным массивом, а  выходным массивом на m+1 ступени вычислений. Таким образом, для случая N=8:
выходным массивом на m+1 ступени вычислений. Таким образом, для случая N=8:
 ;
;  ;
;  ;
; 
 ;
;  ;
;  ;
; 
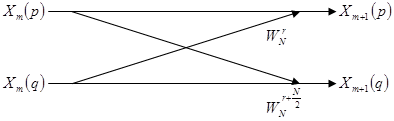
Основным вычислением на графе является вычисление по схеме «бабочка» Рис. 1.8.

Рис. 1.7. Схема 8-точечного БПФ.
Рис. 1.8.
Рис. 1.9.
Уравнение, соответствующее этому графу, имеет вид:
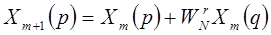
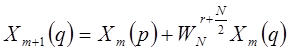
| (1.55)
|
Учитывая, что  , получаем:
, получаем:
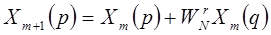

| (1.56)
|
Следовательно, так как имеются N/2 бабочек вида (1.56) на каждую ступень и 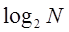 ступеней, общее требуемое число умножений
ступеней, общее требуемое число умножений  . Ясно, что для вычисления элементов p и q m+1-го массива требуются комплексные числа, расположенные на местах p и q m-го массива. Поэтому реально необходим только один комплексный массив из N элементов.
. Ясно, что для вычисления элементов p и q m+1-го массива требуются комплексные числа, расположенные на местах p и q m-го массива. Поэтому реально необходим только один комплексный массив из N элементов.
Чтобы вычисления выполнялись так, как сказано выше, входные данные должны быть записаны в необычном порядке, который называется двоичной инверсией.
Если (n0,n1,n2) – двоичное представление номеров последовательности  , то элемент последовательности x(n2n1n0) запоминается в массиве на месте X(n0n1n2).
, то элемент последовательности x(n2n1n0) запоминается в массиве на месте X(n0n1n2).
 ;
;  ;
;  ;
;
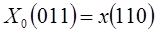 ;
; 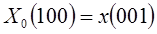 ;
; 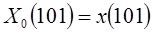 ;
;
 ;
;  .
.
Объяснить этот факт можно с помощью следующей схемы:
Рис. 1.10. 
Двоичная инверсия.
| int math_inverse_bits(int value, int bits)
// инвертируем биты для преобразования Фурье
{
int result = 0;
int mask = 1 << (bits-1);
for (int i=0; i<bits; i++)
{
if (value & mask)
result |= 1 << i;
mask = mask >> 1;
}
return (result);
}
BOOL math_fft(double* dbl_array, int* nSize)
{
// определяем длину для преобразования фурье
int tmp_size = *nSize;
for(int M=0; tmp_size>1; tmp_size/=2,M++);
int fft_size = 1 << M; // 1<<M == 2^M
// подготавливаем массив
std::complex<double>* fft_array =
new std::complex<double>[ fft_size ];
ASSERT(fft_array);
// устанавливаем порядок для fft
for (int i=0; i<fft_size; i++)
{
fft_array[ math_inverse_bits(i,M) ] =
std::complex<double>(dbl_array[ i ],0.0);
}
double pi = 3.141592653589793;
// M этапов
for (int l=0; l<M; l++)
{
int le = 1 << (l+1); // le - смещение между бабочками
int le1 = le >> 1; // le1 - размер бабочки
std::complex<double> U (1.0, 0.0);
std::complex<double> W (cos(pi / le1), sin(pi / le1));
for (int j=0; j<le1; j++)
{
for (int i=j; i<fft_size; i+=le)
{
int ip = i + le1;
std::complex<double> T = fft_array[ ip ] * U;
fft_array [ ip ] = fft_array[ i ] - T;
fft_array [ i ] = fft_array[ i ] + T;
}
U *= W;
}
}
for (i=0; i<fft_size / 2; i++)
{
dbl_array[ i ] = std::abs(fft_array[ i ]);
}
*nSize = fft_size / 2;
delete[] fft_array; fft_array = NULL;
return (TRUE);
}
|
Рис. 1.11. Пример программы БПФ на языке C++.



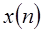 на меньшие подпоследовательности, называются алгоритмами с прореживанием по времени.
на меньшие подпоследовательности, называются алгоритмами с прореживанием по времени. .
.  ,
,  . Разделим
. Разделим  , или, заменяя индексы суммирования на
, или, заменяя индексы суммирования на  при четном n и
при четном n и  при нечетном, получим
при нечетном, получим  =
=  , т.к.
, т.к.  , то
, то =
= 
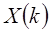 .
.


 .
. раз, определяя в результате дискретное преобразование Фурье. Обозначим последовательность комплексных чисел, получающихся на m-ой ступени вычисления, через
раз, определяя в результате дискретное преобразование Фурье. Обозначим последовательность комплексных чисел, получающихся на m-ой ступени вычисления, через 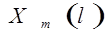 , где
, где 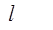 =
=  и m=1,2,…
и m=1,2,…  . Можно считать
. Можно считать  входным массивом, а
входным массивом, а  выходным массивом на m+1 ступени вычислений. Таким образом, для случая N=8:
выходным массивом на m+1 ступени вычислений. Таким образом, для случая N=8: ;
;  ;
;  ;
; 
 ;
;  ;
;  ;
; 


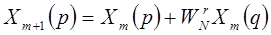
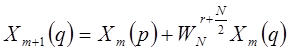
 , получаем:
, получаем: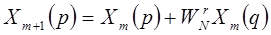

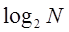 ступеней, общее требуемое число умножений
ступеней, общее требуемое число умножений  . Ясно, что для вычисления элементов p и q m+1-го массива требуются комплексные числа, расположенные на местах p и q m-го массива. Поэтому реально необходим только один комплексный массив из N элементов.
. Ясно, что для вычисления элементов p и q m+1-го массива требуются комплексные числа, расположенные на местах p и q m-го массива. Поэтому реально необходим только один комплексный массив из N элементов. , то элемент последовательности x(n2n1n0) запоминается в массиве на месте X(n0n1n2).
, то элемент последовательности x(n2n1n0) запоминается в массиве на месте X(n0n1n2). ;
;  ;
;  ;
;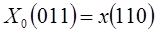 ;
; 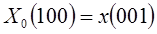 ;
; 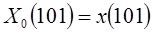 ;
; ;
;  .
.



