Пусть на плоскости  задана плоская фигура
задана плоская фигура  , и пусть непрерывная функция
, и пусть непрерывная функция  - плотность распределения ее массы. Разобьем фигуру на части
- плотность распределения ее массы. Разобьем фигуру на части  сетью гладких кривых и, предполагая, что в пределах одной части плотность распределения масс постоянна, получаем приближенное выражение для массы:
сетью гладких кривых и, предполагая, что в пределах одной части плотность распределения масс постоянна, получаем приближенное выражение для массы:
 .
.
В пределе имеем
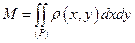 .
.
Аналогично выводятся формулы для статических моментов первого порядка  и
и  относительно осей
относительно осей  и
и  :
:
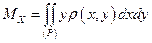 и
и  ,
,
Координаты центра тяжести пластинки вычисляются по формулам:

 .
.
Вторые статические моменты (моменты инерции относительно осей  и
и  ) вычисляются по формулам:
) вычисляются по формулам:
 и
и  .
.
Наконец, момент инерции относительно начало координат имеет вид
 .
.
2. Механические приложения тройного интеграла
Аналогично двумерному случаю можно выписать следующие формулы.
Масса тела:
 .
.
Первые статические моменты относительно координатных плоскостей:

Координаты центра тяжести
 .
.
Вторые статические моменты:

 .
.
ЛЕКЦИЯ 7
Криволинейный интеграл 1-го рода. Его свойства, вычисление, приложения
1. Криволинейный интеграл 1-го рода. Его свойства, вычисление
Пусть в  параметрически задана кривая
параметрически задана кривая  .
.
Будем предполагать, что кривая является гладкой(кусочно-гладкой), т.е функции  непрерывно дифференцируемые:
непрерывно дифференцируемые:  . Такая кривая является спрямляемой. В этом случае длину дуги части кривой, отвечающей отрезку
. Такая кривая является спрямляемой. В этом случае длину дуги части кривой, отвечающей отрезку  можно вычислять при помощи формулы
можно вычислять при помощи формулы
 .
.
Если  -длина части кривой, отвечающей отрезку
-длина части кривой, отвечающей отрезку 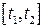 .
.
Пусть  -разбиение отрезка
-разбиение отрезка  ,
,  -
-  разметка разбиения,
разметка разбиения,
 .
.
Образуем интегральную сумму
 .
.
Будем говорить, что для функции  существует криволинейный интеграл первого рода по кривой
существует криволинейный интеграл первого рода по кривой  , если существует
, если существует  , не зависящий от
, не зависящий от  . Т.е
. Т.е 
Значение интеграла полагают равным числу А:
 .
.
Свойства криволинейного интеграла 1-го рода:
1. 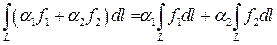 .
.
2. Если  .
.
3.Если  на
на  , то
, то  .
.
4.  ,
,
где  - длина
- длина 
Вычисление криволинейного интеграла 1-го рода.
По определению интеграла сумма  является интегральной суммой для интеграла Римана-Стилтьеса
является интегральной суммой для интеграла Римана-Стилтьеса  поэтому
поэтому  .
.
Если  ,
,  - гладкая кривая, то
- гладкая кривая, то 

Если кривая  задана в трехмерном пространстве
задана в трехмерном пространстве

 , то аналогично
, то аналогично

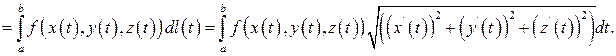
2. Приложения криволинейного интеграла 1-го рода
Геометрическое приложение: Вычисление длины кривой.
Длина кривой 
Механические приложения: Вычисление массы, статических моментов, координат центра тяжести.
Пусть сначала  - плоская кривая
- плоская кривая  - плотность на кривой
- плотность на кривой  . Имеют место следующие формулы:
. Имеют место следующие формулы:
Масса
 .
.
Первые статические моменты относительно осей  и
и 

Координаты центра тяжести
 .
.
Вторые статические моменты (моменты инерции) относительно осей  и
и 

Момент инерции относительно начала координат
 .
.
Пусть теперь  - пространственная кривая,
- пространственная кривая,  -плотность на кривой
-плотность на кривой  . Имеют место следующие формулы:
. Имеют место следующие формулы:
Масса
 .
.
Первые статические моменты относительно координатных плоскостей

Координаты центра тяжести
 .
.
Вторые статические моменты (моменты инерции) относительно координатных плоскостей:

Момент инерции относительно начала координат

ЛЕКЦИЯ 8
Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в R2
1. Криволинейный интеграл 2-го рода. Его физический смысл
Пусть  - гладкая кривая,
- гладкая кривая,
 .
.
Пусть  - разбиение отрезка
- разбиение отрезка  ,
,
 - мелкость разбиения,
- мелкость разбиения,
 -
-  разметка разбиения.
разметка разбиения.
Образуем следующую интегральную сумму:
 Будем говорить, что для функций
Будем говорить, что для функций  существует криволинейный интеграл второго рода по кривой
существует криволинейный интеграл второго рода по кривой  в направлении возрастания параметра
в направлении возрастания параметра  (от начальной точки кривой к конечной точке), если существует
(от начальной точки кривой к конечной точке), если существует  , не зависящий от
, не зависящий от  , т.е.
, т.е.

Этой интеграл имеет следующее обозначение
 .
.
Он зависит от ориентации кривой

В случае замкнутой кривой различают положительную и отрицательную ориентацию: против часовой стрелки и по часовой стрелке.
Этот случай подчеркивают следующим обозначением
 .
.
Функции  в записи интеграла можно считать координатами вектора
в записи интеграла можно считать координатами вектора  . Его называют векторным полем, заданным на кривой
. Его называют векторным полем, заданным на кривой  .
.
Обозначим 
Криволинейный интеграл  определяет работу векторного (силового) поля
определяет работу векторного (силового) поля 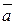 вдоль кривой
вдоль кривой  в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией.
в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией.
2. Формула Грина
Теорема (Формула Грина). Пусть в односвязной области  задано векторное поле
задано векторное поле  таким, что функции
таким, что функции  - непрерывные в Е.Кривая
- непрерывные в Е.Кривая  , множество
, множество  , ограниченное этой кривой выпуклое. Тогда справедлива формула
, ограниченное этой кривой выпуклое. Тогда справедлива формула
 .
.
Здесь кривая  обходится в положительном направлении.
обходится в положительном направлении.
Доказательство. Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
 y
y
y = y2(x)
D
A
C
B
y= y1(x)
0 x1 x2 x
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:


Рассуждая аналогично, для области правильной при проектировании на ось 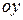 , получим
, получим
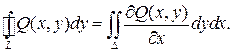 (2)
(2)
Складывая (1) и (2), получим формулу Грина.
3. Условия независимости интеграла от пути в R 2
Лемма. Работа векторного поля не зависит от пути тогда и только тогда, когда любая циркуляция равна 0.
Доказательство. Пусть  произвольный замкнутый контур, точки А и В – любые точки на
произвольный замкнутый контур, точки А и В – любые точки на  . Тогда
. Тогда
 .
.
Работа векторного поля не зависит от пути  .
.
Лемма доказана.
Векторное поле  называется потенциальным, если существует функция 2-х переменных
называется потенциальным, если существует функция 2-х переменных  - скалярное поле такое, что
- скалярное поле такое, что  ,т.е
,т.е  .
.
Замечание. В дифференциальных уравнениях уравнение первого порядка, записанное в дифференциалах  называется уравнением в полных дифференциалах, если существует скалярное поле
называется уравнением в полных дифференциалах, если существует скалярное поле  :
:  .
.
В этом случае общий интеграл уравнения имеет вид 
Теорема. Если в односвязной области  функции
функции 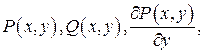
 непрерывны, то следующие условия эквивалентны:
непрерывны, то следующие условия эквивалентны:
1) поле  - потенциальное в
- потенциальное в  ;
;
2)  в
в  ;
;
3) Работа поля  в
в  не зависит от пути.
не зависит от пути.
Доказательство. Будем следовать схеме  .
.
· 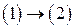
Поле  - потенциальное в
- потенциальное в  , поэтому
, поэтому 
 -скалярное поле:
-скалярное поле:  , т.е.
, т.е. 
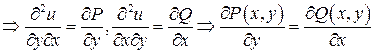 .
.
· 
Достаточно проверить, что любая циркуляция в  равна 0.
равна 0.
Используем формулу Грина, получим
 .
.
· 
Покажем, что следующее скалярное поле и есть искомый потенциал:

Итак,



 -потенциальное поле в
-потенциальное поле в  .
.
ЛЕКЦИЯ 9
Площадь поверхности в R3. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения
1. Площадь поверхности в R 3
Поверхность в  задается параметрически при помощи 2 параметров
задается параметрически при помощи 2 параметров

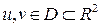 ,
,
 ,
,
 - поверхность в
- поверхность в  .
.
Иногда поверхность задают при помощи одной функции двух переменных
 .
.
Поверхность  называется гладкой если:
называется гладкой если:
 .
.
Из этих частных производных можно записать матрицу Якоби нашего отображения
 .
.
Точку  назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми.
назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми.
Выясним геометрический смысл этих векторов. Эти векторы  - касательные векторы к линиям
- касательные векторы к линиям  на поверхности. В не особой точке эти касательные векторы не коллинеарные.
на поверхности. В не особой точке эти касательные векторы не коллинеарные.
Можно показать, что все касательные векторы к кривым на поверхности, проходящие через 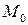 , лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке
, лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке 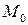 .
.
В не особой точке уравнение касательной плоскости можно записать с помощью точки 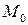 и двух касательных векторов
и двух касательных векторов  :
:
 .
.
Рассмотрим вектор  .
.
Очень часто в качестве нормального вектора будем использовать единичный нормальный вектор

Определим первую квадратную форму на поверхности. Пусть



Таким образом, п ервая квадратичная форма на поверхности имеет вид:
 .
.
Определение. Площадью гладкой поверхности  ,
,  -измеримо по Жордану, называется число:
-измеримо по Жордану, называется число:  .
.
Преобразуем эту формулу для площади поверхности
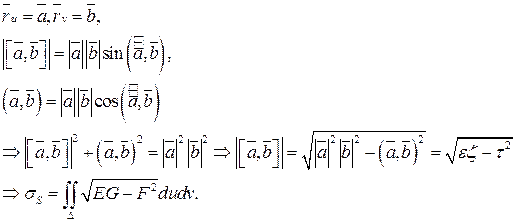
2. Поверхностный интеграл 1-го рода. Его свойства, вычисление
Пусть поверхность  ,
, 
 - непрерывная функция.
- непрерывная функция.
Определение. Поверхностным интегралом первого рода по поверхности  от функции
от функции  называется число
называется число
 .
.
Здесь  - элемент площади поверхности.
- элемент площади поверхности.
Данное определение справедливо и для кусочно-гладкой поверхности, т.е. поверхности, которая может быть разбита на конечное число гладких участков.
Поверхностный интеграл первого рода сводится к некоторому двойному интегралу и для него справедливы все его свойства.
3. Приложения поверхностного интеграла 1-го рода
Геометрическое приложение: Вычисление площади поверхности 
Механические приложения: Вычисление массы, статических моментов, координат центра тяжести поверхности, начиненной веществом с плотностью  .
.
Масса:  .
.
Первые статические моменты относительно координатных плоскостей:

Координаты центра тяжести:
 .
.
Вторые статические моменты относительно координатных плоскостей:
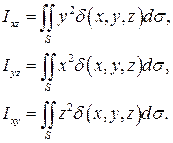
Статический момент (момент инерции) относительно начала координат:
 .
.
ЛЕКЦИЯ 10



 задана плоская фигура
задана плоская фигура  , и пусть непрерывная функция
, и пусть непрерывная функция  - плотность распределения ее массы. Разобьем фигуру на части
- плотность распределения ее массы. Разобьем фигуру на части  сетью гладких кривых и, предполагая, что в пределах одной части плотность распределения масс постоянна, получаем приближенное выражение для массы:
сетью гладких кривых и, предполагая, что в пределах одной части плотность распределения масс постоянна, получаем приближенное выражение для массы: .
.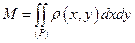 .
. и
и  относительно осей
относительно осей  и
и  :
: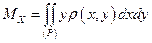 и
и  ,
,
 .
. и
и  .
. .
. .
.
 .
.
 .
. параметрически задана кривая
параметрически задана кривая  .
. непрерывно дифференцируемые:
непрерывно дифференцируемые:  . Такая кривая является спрямляемой. В этом случае длину дуги части кривой, отвечающей отрезку
. Такая кривая является спрямляемой. В этом случае длину дуги части кривой, отвечающей отрезку  можно вычислять при помощи формулы
можно вычислять при помощи формулы .
. -длина части кривой, отвечающей отрезку
-длина части кривой, отвечающей отрезку 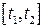 .
. -разбиение отрезка
-разбиение отрезка  ,
,  -
-  разметка разбиения,
разметка разбиения, .
. .
. существует криволинейный интеграл первого рода по кривой
существует криволинейный интеграл первого рода по кривой  , если существует
, если существует  , не зависящий от
, не зависящий от  . Т.е
. Т.е 
 .
.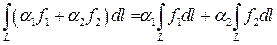 .
. .
. на
на  .
. ,
, - длина
- длина 
 является интегральной суммой для интеграла Римана-Стилтьеса
является интегральной суммой для интеграла Римана-Стилтьеса  поэтому
поэтому  .
. ,
, 


 , то аналогично
, то аналогично
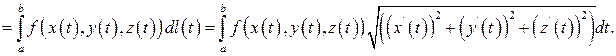

 - плотность на кривой
- плотность на кривой  .
.
 .
.
 .
. -плотность на кривой
-плотность на кривой  .
.
 .
.

 .
. - мелкость разбиения,
- мелкость разбиения, Будем говорить, что для функций
Будем говорить, что для функций  существует криволинейный интеграл второго рода по кривой
существует криволинейный интеграл второго рода по кривой  (от начальной точки кривой к конечной точке), если существует
(от начальной точки кривой к конечной точке), если существует  , не зависящий от
, не зависящий от 
 .
.
 .
. . Его называют векторным полем, заданным на кривой
. Его называют векторным полем, заданным на кривой  .
.
 определяет работу векторного (силового) поля
определяет работу векторного (силового) поля 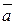 вдоль кривой
вдоль кривой  в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией.
в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией. задано векторное поле
задано векторное поле  - непрерывные в Е.Кривая
- непрерывные в Е.Кривая  , множество
, множество  , ограниченное этой кривой выпуклое. Тогда справедлива формула
, ограниченное этой кривой выпуклое. Тогда справедлива формула .
. y
y

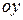 , получим
, получим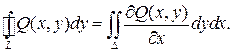 (2)
(2) .
. .
. - скалярное поле такое, что
- скалярное поле такое, что  ,т.е
,т.е  .
. называется уравнением в полных дифференциалах, если существует скалярное поле
называется уравнением в полных дифференциалах, если существует скалярное поле  .
.
 функции
функции 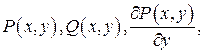
 непрерывны, то следующие условия эквивалентны:
непрерывны, то следующие условия эквивалентны: в
в  .
.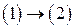

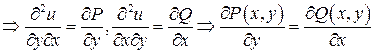 .
.
 .
.




 задается параметрически при помощи 2 параметров
задается параметрически при помощи 2 параметров
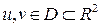 ,
, ,
, - поверхность в
- поверхность в  .
. называется гладкой если:
называется гладкой если: .
. .
. назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми.
назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми. - касательные векторы к линиям
- касательные векторы к линиям  на поверхности. В не особой точке эти касательные векторы не коллинеарные.
на поверхности. В не особой точке эти касательные векторы не коллинеарные.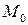 , лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке
, лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке  :
: .
. .
.



 .
. ,
,  -измеримо по Жордану, называется число:
-измеримо по Жордану, называется число:  .
.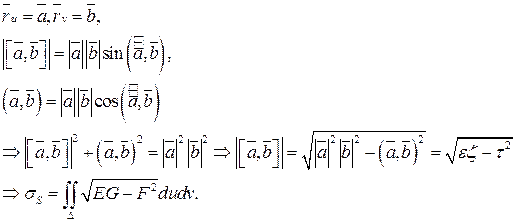
 ,
, 
 - непрерывная функция.
- непрерывная функция. от функции
от функции  называется число
называется число .
. - элемент площади поверхности.
- элемент площади поверхности.
 .
. .
.
 .
.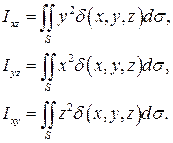
 .
.


