Для характеристики интенсивности изменения явления во времени необходимо рассчитать следующие показатели: абсолютные приросты, темпы роста и прироста, а также средние показатели. Все эти показатели определяются по формулам:
1 Абсолютный прирост – показывает, насколько изменяется уровень ряда в сравнении с первым или предыдущим значением.
DyiБ=yi– y1 (8)
DyiЦ= yi– yi-1 (9)
2 Темп роста – характеризует интенсивность изменений уровней ряда.
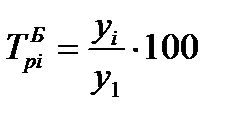 (10)
(10)
 (11)
(11)
3Темп прироста – характеризует скорость изменения уровней ряда, насколько процентов больше 0 возрастает, меньше 0 убывает.
 (12)
(12)
4 Абсолютное значение одного процента прироста: сколько единиц измерения изучаемого показателя на 1% прироста.
А% = Dyц/ Tпpц = 0,01* yi–-1 (13)
Эти показатели характеризуют последовательные изменения уровней ряда от периода к периоду. Для характеристики изменения в целом за весь период применяются следующие показатели.
5 Средний абсолютный прирост – показывает, насколько в среднем изменяются уровни ряда.
 (14)
(14)
где yn – последний уровень.
6 Средний темп роста – средняя интенсивность изменения уровней ряда.
 (15)
(15)
7 Средний темп прироста – характеризует относительную скорость изменения уровней ряда.
 (16)
(16)
8 Средний уровень ряда – определяет среднее значение признака, приходящееся на 1 времени (таблица 10).
Таблица 10
Формулы для расчета среднего уровня ряда
| Вид ряда динамики
| Название средней величины
| Формула средней величины
| Номер формулы
|
| Равномерный интервальный
| Арифметическая простая
| 
| (17)
|
| Равномерный моментный
| Хронологическая простая
| 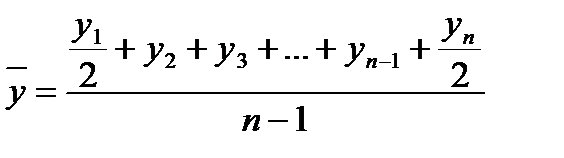
| (18)
|
| Неравномерный интервальный
| Арифметическая взвешенная
| 
| (19)
|
| Неравномерный моментный
| Хронологическая взвешенная
| 
| (20)
|
При изучении динамики явления необходимо выделить в ряде динамики основную тенденцию (общее направление развития) методом аналитического выравнивания – построить модель тренда как функцию от времени. Тип модели тренда определяется графически с помощью построения линейной диаграммы фактических уровней ряда динамики.
В качестве функций (моделей тренда) используются уравнение прямой, параболы, гиперболы, экспоненты и др.ft = a0 +a1 *t – прямая; ft = a0 +a1 *t + a2 *t2. – парабола и т.д., где t – время; y – уровни ряда;
ft– значение уровня ряда, полученное по модели; a0 , a1 , a2 – параметры модели, определяемые из системы нормальных уравнений.
Задача аналитического выравнивания сводится к следующему – определение на основе фактических данных формы (вида) гипотетической функции 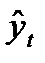 = f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя; нахождение по эмпирическим данным параметров указанной функции (уравнения); расчет по найденному уравнению теоретических (выравненных) уровней.К качестве моделей наиболее часто применяются функции (таблица 11).
= f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя; нахождение по эмпирическим данным параметров указанной функции (уравнения); расчет по найденному уравнению теоретических (выравненных) уровней.К качестве моделей наиболее часто применяются функции (таблица 11).
Таблица 11
Функции для модели тренда
| Название функции
| Вид функции
| Формула
|
| Прямая линия
|
|  (1) (1)
|
| Парабола 2-го порядка
| или
| 
|
| Парабола 3-го порядка
| 5 BnGq5yrlDcKN1iCLXP73F0cAAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAA AAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACU AQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEA5hxlsZsDAACJ CAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAbJjPed0A AAAHAQAADwAAAAAAAAAAAAAAAAD1BQAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAP8G AAAAAA== " path="m,435c130,262,260,90,389,90v129,,251,360,388,345c914,420,1132,77,1212,e" filled="f">
| 
|
| Гипербола
|
| 
|
| Показательная
|
| 
|
| Степенная
|
| 
|
Тип модели определяется графически или с помощью абсолютного прироста и темпа роста. Если абсолютные приросты (цепные) приблизительно одинаковы, то берется линейная модель. Если темпы роста приблизительно одинаковы, то берется степенная (возрастает) или гиперболическая (убывает).
Параметры модели ai рассчитываются методом наименьших квадратов, суть которого состоит в том, чтобы сумма квадратов отклонений фактических данных и полученных по модели должна быть минимальна.
При нахождении минимума функции получается системы нормальных уравнений. Для упрощения расчетов показатель времени t задается так, чтобы сумма по времени равнялась 0 (отчет времени с середины ряда динамики). Например:
Уровни t
четное нечетное
y1 -5 -2
y2 -3 -1
y3 -1 0
y4 1 1
y5 3 2
y6 5 ∑t =0
∑t=0
После такого задания времени системы нармальных уравнений для моделей примут вид:
Для линейной модели:

 (21)
(21)
Для параболы:
 (22)
(22)
Для характеристики качества модели определяют
1) стандартную ошибку модели:
 (23)
(23)
n – число уровней
k – число параметров модели.
2) относительную ошибку модели, характеризующую среднюю степень разброса фактических данных вокруг модели:
 (24)
(24)
Если Vσ< 15%, то модель является хорошей, ее можно использовать для прогнозирования. Для построения прогноза по тренду необходимо в полученную модель подставить будущее значение времени.
Пример 4. Проанализируем изменение товарооборота при помощи показателей динамики (таблица 12).
Таблица 12
Аналитические показатели динамики
| Годы
| Уi
| Абсолютный прирост
| Темп роста
| Темп прироста
| абсолютное значение 1% цепного прироста
|

|   
| 
| 
| 
| 
|
|
|
| -
| -
| -
| -
| -
| -
| -
|
|
|
|
|
| 103,8
| 103,8
| 3,8
| 3,8
| 4,16
|
|
|
|
|
| 101,9
| 105,8
| 1,9
| 5,8
| 4,32
|
|
|
|
|
| 102,3
| 108,2
| 2,3
| 8,2
| 4,4
|
|
|
|
|
| 103,6
|
| 3,6
| 12,0
| 4,5
|
| Итого:
|
|
| -
| Пр =112
| -
| -
| -
| 17,38
|
Рассчитаем средние показатели динамики:
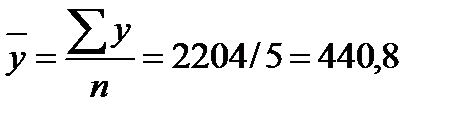
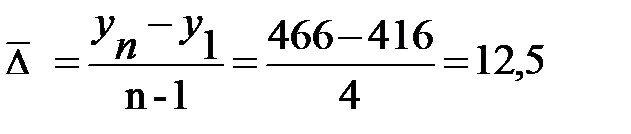


Вывод: Таким образом, товарооборот по региону за 2001-2005 гг. увеличился в целом на 50 млн. руб. (12%), причем ежегодно он увеличивался от 8 млн. руб. (1,9%) до 16 млн. руб. (3,8%). В среднем в год товарооборот составлял млн. руб., он увеличивался в среднем в год на 12,5 млн. руб. (2,9%)
Пример 5. Имеются данные о потреблении овощей на одного члена семьи по району за 2000 –2006 гг. (таблица 14).
Таблица 14
Данные по потреблению овощей на одного человека в год за 2000-2006 гг.
| Год
|
|
|
|
|
|
|
|
| У(t)
| 10,0
| 10,5
| 12,0
| 10,2
| 13,0
| 16,3
| 18,0
|
Построить модель тренда методом аналитического выравнивания по прямой.
Решение:
Для определения параметров модели построим расчетную таблицу 15.
Таблица 15
Расчет параметров модели
| Год
| Потребление овощей, кг.
yt
| t
| t2
| yi*t
| ft= 13 +
+1,3*t
| et = (yt– ft)
| et2=(yt–ft)2
|
|
|
|
|
|
|
|
|
|
|
| 10,0
| -3
|
| -30,0
| 9,1
| 0,9
| 0,81
|
|
| 10,5
| -2
|
| -21,0
| 10,4
| 0,1
| 0,01
|
|
| 12,0
| -1
|
| -12,0
| 11,7
| 0,3
| 0,09
|
|
| 11,2
|
|
|
| 13,0
| -0,8
| 0,64
|
|
| 13,0
|
|
| 13,0
| 14,3
| -1,3
| 1,69
|
|
| 16,3
|
|
| 32,6
| 15,6
| 0,7
| 0,49
|
|
| 18,0
|
|
|
| 16,9
| 1,1
| 1,21
|
| Итого
|
|
|
| 36,6
|
| –
| 4,94
|
По данным расчетной таблицы 15 (столбец 2) определим параметры линейной модели тренда yt = a0 +a1 *t.

Рассчитаем значения ft по построенной модели ft = 13 + 1,3*t.
Расчетные данные приведены в таблице 15 (столбец 6). Для наглядного представления основной тенденции развития явления строится график фактических данных и модели тренда (рис.1).

Рис. 1 - Модель тренда потребления овощей
Для оценки качества модели рассчитываются отклонения от тренда et и сумма квадратов отклонений от тренда et2 (колонка 7 и 8 таблицы 15), а также абсолютная и относительная меры колеблемости отклонений от тренда (остатков):
Стандартная ошибка модели равна

Где к – число параметров в модели, n – число уровней ряда.
Относительная ошибка модели равна

Вывод: Таким образом, относительная мера колеблемости остатков меньше 10 %, следовательно, построенная модель является достаточно хорошей.
Пример 6. Имеются данные о производстве продукции по предприятию (тыс. шт.) за 2000 – 2008 гг. (таблица 16).
Таблица 16
Динамика производства продукции по предприятию за 2000-2008 гг.
Построить модель тренда методом аналитического выравнивания по параболе, оценить ее качество и построить прогноз на 2010 г.
Решение:
Для определения параметров модели построим расчетную таблицу 17.
Таблица17
Расчет параметров модели
| Год
| Производство продукции тыс. шт.
yi
| t
| t2
| yi*t
| t4
| yi*t2
| ft
| (yt–ft)2
|
|
|
| -4
|
| -60
|
|
| 14,7
| 0,09
|
|
|
| -3
|
| -42
|
|
|
|
|
|
|
| -2
|
| -24
|
|
| 11,9
| 0,01
|
|
|
| -1
|
| -9
|
|
| 11,4
| 5,76
|
|
|
|
|
|
|
|
| 11,5
| 0,25
|
|
|
|
|
|
|
|
| 12,2
| 3,24
|
|
|
|
|
|
|
|
| 13,5
| 6,25
|
|
|
|
|
|
|
|
| 15,4
| 5,76
|
|
|
|
|
|
|
|
| 17,9
| 0,01
|
| Итого
|
|
|
|
|
|
| 121,5
| 22,37
|
По данным расчетной таблицы 17 определим параметры квадратичной модели тренда yt = a0 +a1 *t + a2*t2.

Решая систему уравнений, получим значения параметров – a0 = 11,5, a1=0,4, a2 =0,3. Тогда модель основной тенденции примет вид:
ft = 11,5 +0,4 *t + 0,3*t2.
Рассчитаем значения ytпо построенной модели. Расчетные данные приведены в предпоследней колонке таблицы 17. Для наглядного представления основной тенденции развития явления строится график фактических данных и модели тренда (рис. 2). Для оценки качества модели рассчитывается сумма квадратов отклонений от тренда (последняя колонка таблицы 17), а также абсолютная и относительная меры колеблемости отклонений от тренда (остатков):

Рис. 2 - Динамика производства продукции по предприятию
за 2000-2008 гг.
Стандартная ошибка модели равна 
Где к – число параметров в модели, n – число уровней ряда.
Средний уровень ряда равен 
Относительная ошибка модели равна

Вывод: Таким образом, относительная мера колеблемости остатков меньше 15 %, следовательно, построенная модель может быть использована для прогнозирования.
Построим прогноз продукции предприятия на 2010 г. по построенной модели тренда. Так как в 2010 г. время t будет равняться 6, то прогноз равен:
Y* 2004 = 11,5 + 0,4 *6 + 0,3* 36 = 24,7 тыс. шт.
Экономические индексы
Индекс – относительный показатель, выражающий соотношение величин какого-либо явления во времени, пространстве или в сравнении с эталоном, планом. Индекс показывает во сколько раз уровень явления в одних условиях больше или меньше уровня такого же явления в других условиях.
Основным элементом в индексе является индексируемая величина, то есть показатель изменение которого изучается. Индекс называется также как и индексируемая величина. Все показатели в индексном анализе делятся на:
ü количественные (объемные) – они выражают объемы явлений;
ü качественные – они рассчитываются на одну единицу.
Обозначения:
I – общий индекс;
i – индивидуальный индекс;
q – объем производства (продаж) в натуральных единицах;
p – цена единицы продукции;
pq – товарооборот (стоимость);
z – себестоимость единицы продукции;
zq – затраты;
w – выработка на единицу времени (1 работника);
t – трудоемкость;
T=tq – общие затраты труда.
Классификация индексов
Индексы делятся: по характеру индексируемой величины на качественные и количественные; по охвату единиц совокупности на индивидуальные – изучают 1 ед. (товар и т.д.) и общие (сводные) – изучают группу товаров; по базе сравнения на динамические, территориальные, индексы плана, индексы выполнения плана.
Общие индексы делятся п о форме на агрегатные и средние; по составу явлений на индексы переменного состава, фиксированного состава и структуры.
Индивидуальные индексы совпадают с относительными показателями динамики сравнения или плана.
 ;
;  ;
;  ;
;  ;
;  . (25)
. (25)
Общие индексы применяются для изучения динамики различных показателей по группе товаров или для изучения динамики одного товара, реализуемого в различных местах. Так как складывать объемы продаж и цены различных товаров нельзя, то необходимо привести их к сопоставимому виду. Для этого умножают данный показатель на общий соизмеритель, этот соизмеритель называется весом индекса. Общие индексы в статистике наиболее часто строятся в агрегатной форме.
Агрегатный индекс – это соотношение сумм произведений индексируемой величины на вес, взятых в соответствующих периодах.
Примеры агрегатных индексов:
1. Индекс цен  (26)
(26)
Этот индекс показывает, как изменяется стоимость товарной группы под влиянием изменения цен каждого товара.  - на сколько процентов.
- на сколько процентов.  – разность числителя и знаменателя показывает абсолютное изменение стоимости или эффект (перерасход) покупателя от изменения цен.
– разность числителя и знаменателя показывает абсолютное изменение стоимости или эффект (перерасход) покупателя от изменения цен.
2. Индекс физического объема.  (27)
(27)
Этот индекс показывает, как изменяется стоимость товарной группы под влиянием изменения объемов производства (объема продаж). 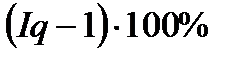 - на сколько процентов.
- на сколько процентов.  - показывает абсолютный эффект изменения от изменения объема продаж.
- показывает абсолютный эффект изменения от изменения объема продаж.
3. Индекс товарооборота.  (28)
(28)
Этот индекс показывает, как изменяется стоимость товарной группы фактически под влиянием изменения и цен и объемов производства (объема продаж). 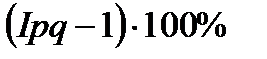 - на сколько процентов.
- на сколько процентов.  - показывает, как изменяется стоимость товарной группы фактически в отчетном периоде по сравнению с базисным.
- показывает, как изменяется стоимость товарной группы фактически в отчетном периоде по сравнению с базисным.
Взаимосвязь индексов имеет вид: 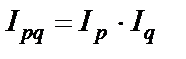 ,
,  (29)
(29)
Пример 7. Имеются данные о реализации плодово-ягодной продукции по району (таблица 18). Определить индивидуальные и общие индексы цен физического объема и товарооборота.
Таблица 18
Данные о реализации товаров за июль-август по району
| Товар
| Июль
| Август
| Расчет
|
| Товарооброт, тыс. руб.
| Продано, тонн
| Товарооброт, тыс. руб.
| Продано, тонн
| p0
| p1
| p0q1
|
| p0q0
| q0
| p1q1
| q1
|
| Черешня
|
|
|
|
|
|
|
|
| Персики
|
|
|
|
|
|
|
|
| Виноград
|
|
|
|
|
|
|
|
| Итого
|
| -
|
|
| -
| -
|
|
Решение: Для расчета индивидуальных индексов построим расчетную таблицу 19.
Таблица 19
Расчет индивидуальных индексов
| Товар
| Исходные данные
| Индивидуальные
индексы
|
| p0q0
| p1q1
| q0
| q1
| p0
| p1
| ip=p1/p0
| iq=q1/q0
| ipq=ip*iq
|
| Черешня
|
|
|
|
|
|
|
| 0,833
| 0,833
|
| Персики
|
|
|
|
|
|
| 0,909
| 1,227
| 1,116
|
| Виноград
|
|
|
|
|
|
| 0,777
| 1,200
| 0,933
|
Вывод 1: Таким образом, по черешне цена в августе по сравнению с июлем не изменилась, реализация снизилась на 16.7%, в результате товарооборот снизился на 16,7%. По персикам цена снизилась на 9,1%, реализация увеличилась на 22,7%, в результате товарооборот увеличился на 11,6%. По винограду цена снизилась на 22,3%, реализация увеличилась на 20%, в результате товарооборот снизился на 6,7%.
Рассчитаем общие индексы

 = -10,8%
= -10,8%
 = 618 – 693= –75 тыс. руб.
= 618 – 693= –75 тыс. руб.

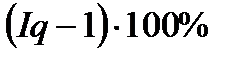 = +8,6%
= +8,6%
 =693 – 638= 55 тыс. руб.
=693 – 638= 55 тыс. руб.
Ip*Iq=Ipq= 0,892*1,086 = 0,97 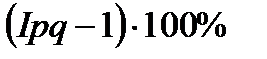 = –3%
= –3%
 = 618 – 638 = –20 тыс. руб.
= 618 – 638 = –20 тыс. руб.
Вывод 2: Товарооборот в целом по данной товарной группе в августе по сравнению с июлемуменьшился на 3,1%или 20 тыс. руб. Под влиянием изменения цен каждого товара товарооборот снизился на 10,8%. Следовательно экономия покупателей от изменения цен составила 75 тыс. руб. Под влиянием изменения реализации каждого товара товарооборот увеличился на 8,6% или на 55 тыс. руб.
Список литературы
Основная литература
1. Ефимова М.Р Социально-экономическая статистика: Учебник для бакалавров / М.Р. Ефимова. – М.: ЮНИТИ-ДАНА, 2012.– 489 с.
2. Теория статистики: Учебник / Под ред. Р.А. Шмойловой – М.: Финансы и статистика, 2001-2008.– 568 с.
Рекомендуемая литература
3. Практикум по теории статистики: Учеб. Пособие/Под ред.
Р. А. Шмойловой. – М.: Финансы и статистика, 2004. – 416 с.
4. Елисеева И. И., Юзбашев М. М. Общая теория статистики: Учебник. – М.: ИНФРА-М, 2007. – 387 с.
5. Экономическая статистика: Учебник/ Под ред. Ю. Н. Иванова. – М.: ИНФРА-М, 2009. – 680 с.
6. Гусаров В. М. Статистика: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2003. – 463 с.
7. Курс социально-экономической статистики: Учебник для вузов /Под ред. проф. М. Г. Назарова. – М.: Финстатинформ, ЮНИТИ-ДАНА, 2005. – 771 с.
8. Статистика: Учебник для вузов /Под ред. Л. П Харченко, В. Г Долженкова, В. Г. Ионина. – М.: ИНФРА-М, 2008. – 311 с.
9. Громыко Г.Л. Теория статистики: Учебник /Г.Л. Громыко – М.: Финансы и статистика, 2003. – 483 с.
10. Салин В.Н., Шпаковская Е.П. Социально-экономическая статистика.: Учебник /В.Н. Салин, Е.П. Шпаковская – М.: Юрист, 2002 – 490 с.
11. Сиденко А.В., Матвеева В.М., Попов Г.Ю. Статистика: Учебник /Под ред.. А.В Сиденко. – М.: «Дело и Сервис», 2000. – 378 с.
Программное обеспечение и Интернет-ресурсы:
15. www.gks.ru / – официальный сайт Федеральной статистической службы
16. www.kemerovostat.ru/-официальный сайт Кемеровского областного комитета по статистике
17. www.nns.ru / – Национальная электронная библиотека.
18. www.,biznes-karta.ru/ – Агентство деловой информации «Бизнес-карта».
19. www.,rbs.ru/ – Информационное агентство «РосБизнесКонсалтинг»
20. www.rambler.ru / – Поисковая система.
21. www.yandex.ru / – Поисковая система.
22 www.test.specialist.ru / – Центр компьютерного обучения МГТУ им. Н.Э Баумана.
Приложение 1
Известны данные по 25 малым предприятиям за отчетный период (таблица 28).
Таблица 28
| Предприятия
| Выпуск продукции,
тыс. шт.
| Полная себестоимость продукции,
тыс. руб.
| Реализованная продукция,
тыс. руб.
|
|
| 3,5
|
|
|
|
| 4,6
|
|
|
|
| 5,5
|
|
|
|
| 4,6
|
|
|
|
| 2,6
|
|
|
|
| 2,0
|
|
|
|
| 7,5
|
|
|
|
| 6,9
|
|
|
|
| 4,1
|
|
|
|
| 4,8
|
|
|
|
| 7,6
|
|
|
|
| 6,5
|
|
|
|
| 11,4
|
|
|
|
| 10,6
|
|
|
|
| 9,0
|
|
|
|
| 6,9
|
|
|
|
| 5,0
|
|
|
|
| 11,2
|
|
|
|
| 8,0
|
|
|
|
| 7,8
|
|
|
|
| 4,2
|
|
|
|
| 6,3
|
|
|
|
| 12,0
|
|
|
|
| 9,8
|
|
|
|
| 8,5
|
|
|
Приложение 2
Известны данные группировки магазинов города по размеру товарооборота (таблица 29).
Таблица 29
| Группы магазинов по товарообороту,
тыс. руб.
| Число магазинов, fi
|
| Варианты
|
|
|
|
|
|
|
|
|
|
|
|
| До 50
|
|
|
|
|
|
|
|
|
|
|
| 50-60
|
|
|
|
|
|
|
|
|
|
|
| 60-70
|
|
|
|
|
|
|
|
|
|
|
| 70-80
|
|
|
|
|
|
|
|
|
|
|
| 80-90
|
|
|
|
|
|
|
|
|
|
|
| 90-100
|
|
|
|
|
|
|
|
|
|
|
| 100-110
|
|
|
|
|
|
|
|
|
|
|
| 110-120
|
|
|
|
|
|
|
|
|
|
|
| 120-130
|
|
|
|
|
|
|
|
|
|
|
| Более 130
|
|
|
|
|
|
|
|
|
|
|
Приложение 3
Имеются данные об остатках товара в магазине на первое число месяца, тыс. руб. (таблица 30).
Таблица 30
| № варианта
| 1.01
| 1.02
| 1.03
| 1.04
| 1.05
| 1.06
| 1.07
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 4
Динамика производства важнейших видов продукции по г. Новокузнецку за 2000-2010 гг. (таблица 31).
Таблица 31
| Показатель
| ГОД
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Агломерат, млн. тонн
|
10,6
|
10,7
|
10,2
|
10,7
|
10,8
|
11,0
|
10,2
|
10,5
|
11,3
|
11,2
|
9,2
|
|
2. Уголь, млн. тонн
|
17,7
|
20,7
|
21,2
|
22,3
|
23,3
|
25,7
|
25,3
|
22,6
|
22,0
|
22,6
|
22,9
|
|
3. Чугун, млн. тонн
|
4,4
|
5,9
|
7,1
|
7,3
|
7,5
|
7,4
|
7,2
|
7,0
|
7,1
|
6,7
|
6,5
|
|
4. Сталь, млн. тонн
|
6,6
|
7,9
|
9,0
|
9,2
|
9,4
|
9,3
|
8,6
|
8,5
|
8,6
|
8,2
|
7,9
|
|
5. Прокат, млн. тонн
|
6,1
|
7,1
|
7,2
|
7,3
|
7,4
|
7,2
|
6,8
|
7,0
|
6,9
|
6,8
|
6,5
|
Приложение 5
Динамика реализации овощей и фруктов на рынках г. Москвы в 2005 г. (таблица 32).
Таблица 32
|
Товар
| Январь
| Февраль
| Март
| Апрель
| Май
|
| Кол-во
продан-ного, кг
| Товаро-
оборот, тыс. руб.
| Кол-во
продан-ного, кг
| Товаро-
оборот, тыс. руб.
| Кол-во
продан-ного, кг
| Товаро-
оборот, тыс. руб.
| Кол-во
продан-ного, кг
| Товаро-
оборот, тыс. руб.
| Кол-во
продан-ного, кг
| Товаро-
оборот, тыс. руб.
|
| q
| pq
| q
| pq
| q
| pq
| q
| Pq
| q
| pq
|
| Капуста
|
| 10,6
|
| 17,7
|
| 14,5
|
| 20,3
|
| 13,7
|
| Свекла
|
| 8,0
|
| 10,1
|
| 8,3
|
| 12,7
|
| 8,9
|
| Морковь
|
| 14,8
|
| 25,0
|
| 22,2
|
| 28,9
|
| 22,7
|
| Огурцы
|
| 12,3
|
| 17,0
|
| 13,5
|
| 18,4
|
| 14,0
|
| Помидоры
|
| 7,2
|
| 9,2
|
| 5,9
|
| 8,9
|
| 5,5
|
| Яблоки
|
| 14,4
|
| 18,1
|
| 7,4
|
| 6,9
|
| 7,5
|
| Фрукты
|
| 42,7
|
| 83,9
|
| 51,2
|
| 58,3
|
| 58,5
|
| Семечки
|
| 12,8
|
| 22,7
|
| 18,2
|
| 23,0
|
| 19,5
|



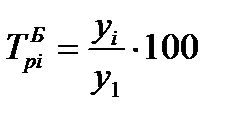 (10)
(10) (11)
(11) (12)
(12) (14)
(14) (15)
(15) (16)
(16)
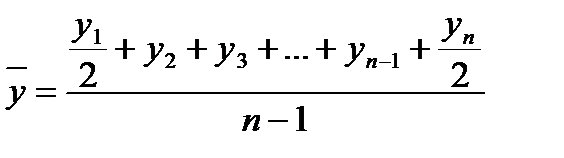


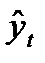 = f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя; нахождение по эмпирическим данным параметров указанной функции (уравнения); расчет по найденному уравнению теоретических (выравненных) уровней.К качестве моделей наиболее часто применяются функции (таблица 11).
= f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя; нахождение по эмпирическим данным параметров указанной функции (уравнения); расчет по найденному уравнению теоретических (выравненных) уровней.К качестве моделей наиболее часто применяются функции (таблица 11). (1)
(1)






 (21)
(21) (22)
(22) (23)
(23) (24)
(24)






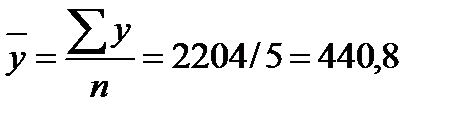
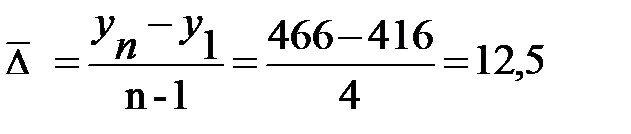











 ;
;  ;
;  ;
;  ;
;  . (25)
. (25) (26)
(26) - на сколько процентов.
- на сколько процентов.  – разность числителя и знаменателя показывает абсолютное изменение стоимости или эффект (перерасход) покупателя от изменения цен.
– разность числителя и знаменателя показывает абсолютное изменение стоимости или эффект (перерасход) покупателя от изменения цен. (27)
(27)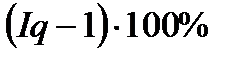 - на сколько процентов.
- на сколько процентов.  - показывает абсолютный эффект изменения от изменения объема продаж.
- показывает абсолютный эффект изменения от изменения объема продаж. (28)
(28)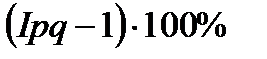 - на сколько процентов.
- на сколько процентов.  - показывает, как изменяется стоимость товарной группы фактически в отчетном периоде по сравнению с базисным.
- показывает, как изменяется стоимость товарной группы фактически в отчетном периоде по сравнению с базисным.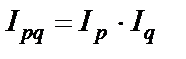 ,
,  (29)
(29)
 = -10,8%
= -10,8%



