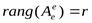http://bodrenko.org/algebra/unit%205_1/unit_5_1.htm
1. Определение линейного оператора. Пусть V и W — линейные пространства, размерности которых равны соответственно n и m. Мы будем называть оператором А, действующим из V в W, отображение вида А: V —> W, сопоставляющее каждому элементу х пространства V некоторый элемент у пространства W. При этом будем использовать обозначение у = А (х) или у = Ах.
Определение. Оператор А, действующий из V в W, называется линейным, если для любых элементов x1 u x2 пространства V и любого комплексного числа λ выполняются соотношения:
1°. λ(x1 u x2) = λx1+ λx2 (свойство аддитивности оператора);
2°. А (λх) = λАх (свойство однородности оператора).
Замечание 1. Если пространство W представляет собой комплексную плоскость, то линейный оператор A, действующий из V в W, называется линейной формой или линейным функционалом.
Замечание 2. Если пространство W совпадает с пространством V, то линейный оператор, действующий в этом случае из V в V, называют также линейным преобразованием пространства V.
2. Действия над линейными операторам. Пространство линейных операторов. В множестве всех линейных операторов, действующих из V в W, определим операции суммы таких операторов и умножения оператора на скаляр.
Пусть А и В — два линейных оператора, действующих из V в W. Суммой этих операторов назовем линейный оператор А + В, определяемый равенством
(А + В)х = Ах + Вх. (5.1)
Произведением линейного оператора А на скаляр λ назовем линейный оператор λА, определяемый равенством
(λА)х= λ(Ах). (5.2)
Назовем нулевым оператор, обозначаемый символом О и отображающий все элементы пространства V в нулевой элемент пространства W.
Иными словами, оператор О действует по правилу Ох = 0.
Для каждого оператора А определим противоположный оператор -А посредством соотношения
-А = (-1)А.
Легко проверить справедливость следующего утверждения.
Множество L(V, W) всех линейных операторов, действующих из V в W, с указанными выше операциями суммы и умножения на скаляр и выбранными нулевым оператором и противоположным оператором образует линейное пространство.
3. Свойства множества L (V, V) линейных операторов. Исследуем подробнее линейные операторы, действующие из V в V, т. е. изучим подробнее множество L(V, V).
Назовем тождественным (или единичным) оператором линейный оператор I, действующий по правилу Iх = х (здесь х — любой элемент V).
Введем понятие произведения линейных операторов из множества L(V, V).
Произведением операторов А и В из L(V, V) называется оператор АВ, действующий по правилу
(АВ)х = А(Вх). (5.3)
Отметим, что, вообще говоря, АВ ≠ ВА.
Справедливы следующие свойства линейных операторов из L(V, V):
1°. λ(АВ) = (λА)В;
2°. (А + В)С = АС + ВС;
3°. А(В + С) = АВ + АС;
4°. (АВ)С = А(ВС).
Первое из свойств 1°-4° следует из определения произведения линейного оператора на скаляр (см. 5.2)) и определения произведения операторов (см. 5.3)).
Перейдем к обоснованию свойства 2°. Имеем, согласно (5.1), (5.2) и (5.3),
((А + В)С)х = (А + В)(Сх) = А(Сх) + В(Сх) = (АС)х + (ВС)х = (АС + ВС)х. (5.4)
Сравнивая левую и правую части последних соотношений, мы получаем равенство (А + В)С = АС + ВС. Свойство 2° установлено.
Совершенно аналогично доказывается свойство 3°.
Свойство 4° справедливо, поскольку, согласно определению (см. (5.3)), произведение линейных операторов заключается в их последовательном действии, и поэтому линейные операторы (АВ)С и А(ВС) совпадают и, следовательно, тождественны.
Замечание 1. Свойство 4° позволяет определить произведение АВ...С любого конечного числа операторов из L(V, V) и, в частности, n-ю степень оператора А с помощью формулы

Очевидно, справедливо соотношение An+m = AnAm.
Нам понадобится понятие обратного оператора для данного оператора А из L(V, V).
Определение 1. Линейный оператор В из L(V, V) называется обратным для оператора А из L(V, V), если выполняется соотношение
АВ = ВА = I.
Обратный оператор для оператора А обычно обозначается символом А-1.
Из определения обратного оператора А следует, что для любого х Є V справедливо соотношение А-1Ах = х.
Таким образом, если А-1Ах = 0, то х = 0, т.е. если оператор А имеет обратный, то из условия Ах = 0 следует, что х = 0.
Мы будем говорить, что линейный оператор А действует взаимно однозначно из V в V, если любым двум различным элементам x1 и x2 отвечают различные элементы y1 = Ax1 и у2 = Аx2.
Если оператор А действует взаимно однозначно из V в V, то отображение А: V —> V представляет собой отображение V на V, т. е. каждый элемент у Є V представляет собой образ некоторого элемента x Є V:
y = Ах.
Чтобы убедиться в этом, достаточно, очевидно, доказать, что n линейно независимых элементов x1,x2,...,xn пространства V отображаются посредством оператора А в n линейно независимых Ax1,Ax2,...,Axn элементов этого же пространства.
Итак, пусть x1,x2,...,xn — линейно независимые элементы V.
Если линейная комбинация α1Ax1+ α2Ax2,...+ αnAxn представляет собой нулевой элемент пространства V:
α1Ax1+ α2Ax2,...+ αnAxn = 0,
то из определения линейного оператора (см. п. 1 этого параграфа) следует, что A(α1x1+ α2x2,...+ αn xn) = 0.
Так как оператор А действует из V в V взаимно однозначно, то из последнего соотношения вытекает, что α1x1+ α2x2,...+ αn xn = 0. Но элементы x1,x2,...,xn линейно независимы. Поэтому α1 = α2=... = αn = 0. Следовательно, элементы Ax1,Ax2,...,Axn также линейно независимы.
Отметим следующее утверждение.
Для того чтобы линейный оператор А из L(V, V) имел обратный, необходимо и достаточно, чтобы этот оператор действовал взаимно однозначно из V в V.
Убедимся, что сформулированное условие необходимо. Пусть оператор А имеет обратный, но не действует взаимно однозначно из V в V.
Это означает, что некоторым различным элементам x1 и x2, x2 - x1 ≠ 0 из V отвечает один и тот же элемент у = Ax1 = Ах2. Но тогда А(x2 - x1) = 0, и поскольку оператор А имеет обратный, x1 - x2= 0. Но выше было отмечено, что x2 - x1 ≠ 0. Полученное противоречие доказывает необходимость условия утверждения.
Докажем достаточность этого условия.
Допустим, что оператор А действует взаимно однозначно из V в V.
Тогда каждому элементу у Є V отвечает элемент х Є V такой, что у = Ах. Поэтому имеется оператор А, обладающий тем свойством, что А-1у = А (Ах) = х. Легко убедиться, что оператор А линейный. По определению А — обратный оператор для оператора А.
Достаточность условия утверждения также доказана.
Введем понятия ядра и образа линейного оператора.
Определение 2. Ядром линейного оператора А называется множество всех тех элементов х пространства V, для которых Ах = 0. Ядро линейного оператора А обозначается символом ker А.
Если ker A = 0, то оператор А действует взаимно однозначно из V в V. Действительно, в этом случае из условия Ах = 0 вытекает х = 0, а это означает, что различным x1 и x2 отвечают различные у1 = Ax1 и у2 = Ах2 (если бы y1 = у2, то А(x2 - x1) = 0, т. е. x1 = х2 и элементы x1 и x2 не были бы различны).
Таким образом, согласно доказанному выше утверждению условие ker A = 0 является необходимым и достаточным для того, чтобы оператор А имел обратный.
Определение 3. Образом линейного оператора А называется множество всех элементов у пространства V, представимых в виде у = Ах. Образ линейного оператора А обозначается символом im A (Символ im следует отличать от символа Im, используемого для обозначения мнимой части комплексного числа).
Замечание 2. Отметим, что если ker А = 0, то im A = V, и наоборот. Поэтому наряду с отмеченным выше условием ker A = 0 условие im A = V также является необходимым и достаточным для того, чтобы оператор А имел обратный.
Замечание 3. Очевидно, ядро ker А и образ im A — л инейные подпространства пространства V. Поэтому можно рассматривать размерности dim (ker А) и dim (imA) этих подпространств.
Справедлива следующая теорема.
Теорема 5.1. Пусть размерность dimV пространства V равна n, и пусть А — линейный оператор из L(V, V). Тогда
dim (im А) + dim (ker A) = n.
Доказательство. Так как ker А представляет собой подпространство V, то можно указать такое подпространство V1 пространства V, что V1 будет представлять собой прямую сумму V и ker A. Согласно теореме 2.10 dim V1 + dim (ker A) = n. Поэтому для доказательства теоремы достаточно убедиться, что dim V1 = dim (im A).
Пусть dimV1 = р, dim(im A) = q и y1,y2,...,yq — базис в im A. Так как линейный оператор А действует взаимно однозначно из V1 в im А, то каждому элементу у из im А можно поставить в соответствие единственный элемент х Є V1 такой, что Ах = у. Поэтому в V1 определены элементы x1,x2,...,xq такие, что Ахk = уk, к = 1, 2,..., q. Элементы x1,x2,...,xq линейно независимы, ибо если α1x1 + α2x2+...+ αqxq = 0, то A(α1x1 + α2x2+...+ αqxq) = α1y1 + α2y2+...+ αqyq = 0, а так как элементы y1,y2,...,yq линейно независимы, то α1 = α2 =... = αq = 0, т. е. и x1,x2,...,xqлинейно независимы. Таким образом, в V1 имеется q линейно независимых элементов. Следовательно, р ≥ q (напомним, что р = dim V1).
Предположим, что р > q. Добавим к линейно независимым элементам x1,x2,...,xq элементы xq+1,xq+2,...,xp так, что x1,x2,...,xp образуют базис в V1. Так как р > q и q = dim (im A), то элементы Ax1,Ax2,...,Axp , принадлежащие im A, линейно зависимы, и поэтому существуют не все равные нулю числа λ1,λ2,...,λp такие, что λ1Ax1 + λ2Ax2 +...+ λpAxp = 0. Отсюда следует, что A(λ1x1 + λ2x2 +...+ λp xp) = 0. Так как А действует из V1 в im A взаимно однозначно, то из последнего равенства получаем λ1x1 + λ2x2 +...+ λp xp = 0.
Но x1,x2,...,xp — базис в V1. Поэтому λ1 = λ2 =... = λp = 0.
Выше указывалось, что не все λ1,λ2,...,λp равны нулю. Следовательно, предположение р > q ведет к противоречию. Таким образом, р = q.
Теорема доказана.
Имеет место также следующая теорема, в определенном отношении обратная теореме 5.1.
Теорема 5.2. Пусть V1и V2— два таких подпространства n-мерного пространства V, что dimV1+dimV2= dim V. Тогда существует такой линейный оператор А из L(V, V), что V1= im A и V2= ker А.
Доказательство. Пусть dim V1 = p, dim V2 = q. Выберем в пространстве V базис е1, е2,..., еn так, чтобы элементы е1, е2,..., еn принадлежали V2. Далее в пространстве V1 выберем некоторый базис g1, g2,..., gp.
Определим теперь значения линейного оператора А на базисных векторах е1, е2,..., еn пространства V следующим образом:
Ae1=g1, Ae2 = g2,..., Аер = gp,
Aep+1 = 0, Аер+2 = 0,..., Аеn = 0.
Далее, если х = x1e1 + x2e2 +... + xpep + xp+1ep+1 +... +xnen,
то Ах = x1g1 + x2g2 +... + xpgp. Очевидно, оператор А линейный и обладает требуемыми свойствами. Теорема доказана.
Введем понятие ранга линейного оператора А.
Назовем рангом линейного оператора А число, обозначаемое символом rang А и равное rang A = dim(im A).
Отметим следующее очевидное следствие из теоремы 5.1 и из замечания 2 этого пункта.
Следствие из теоремы 5.1. Для того чтобы оператор А из L(V, V) имел обратный А-1необходимо и достаточно, чтобы rang A = dim V = n.
Пусть А и В — линейные операторы из L(V, V). Справедлива следующая теорема.
Теорема 5.3. Имеют место следующие соотношения:
rang AB ≤ rang A, rang AB ≤ rang В.
Доказательство. Докажем сначала первое из отмеченных соотношений. Очевидно, im AB  im A. Поэтому dim(im AB) ≤ dim(im A), т.е. rang AB ≤ rang А.
im A. Поэтому dim(im AB) ≤ dim(im A), т.е. rang AB ≤ rang А.
Для доказательства второго соотношения воспользуемся следующим очевидным включением (Так как АВ и ВА различные, вообще говоря, операторы, то включение im AB  im B может не иметь места, и поэтому для доказательства второго соотношения rang AB ≤ rang В требуются специальные рассуждения): ker В
im B может не иметь места, и поэтому для доказательства второго соотношения rang AB ≤ rang В требуются специальные рассуждения): ker В  ker AB.
ker AB.
Из этого включения следует, что dim (ker В) ≤ dim (ker AB).
Из последнего неравенства, в свою очередь, следует неравенство dim V — dim (ker AB) ≤ dimV— dim (ker В), а из него, согласно теореме 5.1, получаем dim(im AB) ≤ dim(im B), т.е. rang AB ≤ rang В.
Теорема доказана.
Докажем еще одну теорему о рангах линейных операторов.
Теорема 5.4. Пусть А и В — линейные операторы из L(V, V) и n — размерность V. Тогда rang AB≥rang A + rang В - n.
Доказательство. Согласно теореме 5.1
dim (im AB) + dim (ker AB) = n. (5.5)
Так как rang AB = dim(im AB), то из (5.5) получаем
rang AB = n - dim (ker AB). (5.6)
Поскольку, согласно теореме 5.1,
dim (ker A) + dim (ker В) = 2n - (rang A + rang В), (5.7)
то для доказательства теоремы достаточно установить неравенство
dim (ker AB) ≤ dim (ker A) + dim (ker B). (5.8)
Действительно, из этого неравенства и из соотношения (5.6) следует неравенство
rang AB ≥ n — (dim (ker A) + dim (kerВ)),
из которого, согласно (5.7), сразу же вытекает справедливость утверждения теоремы.
Итак, перейдем к обоснованию неравенства (5.8). Пусть
dim (ker В) = q. (5.9)
Согласно теореме 5.3 dim (ker AB) ≥ q. Поэтому справедливо соотношение
dim (ker AB) = p + q, где р > 0. (5.10)
Так как ker В  ker AB, то в подпространстве ker AB можно выбрать базис x1,x2,...,xp+q так, что элементы xp+1,...,xp+q образуют базис в ker В. При таком выборе x1,x2,...,xp+q элементы Bx1,Bx2,...,Bxp линейно независимы (если линейная комбинация
ker AB, то в подпространстве ker AB можно выбрать базис x1,x2,...,xp+q так, что элементы xp+1,...,xp+q образуют базис в ker В. При таком выборе x1,x2,...,xp+q элементы Bx1,Bx2,...,Bxp линейно независимы (если линейная комбинация  , а это может быть, в силу выбора x1,x2,...,xp, лишь при λk, = 0, к = 1, 2,..., р). Поэтому элементы Bx1,Bx2,...,Bxp принадлежат ker А, т.е. р ≤ dim (ker А). Из этого неравенства и соотношений (5.9) и (5.10) вытекает требуемое неравенство (5.8). Теорема доказана.
, а это может быть, в силу выбора x1,x2,...,xp, лишь при λk, = 0, к = 1, 2,..., р). Поэтому элементы Bx1,Bx2,...,Bxp принадлежат ker А, т.е. р ≤ dim (ker А). Из этого неравенства и соотношений (5.9) и (5.10) вытекает требуемое неравенство (5.8). Теорема доказана.
Следствие из теорем 5.3 и 5.4. Если rang А = n (n — размерность V), то rang AB = rang ВА = rang В.
Указанное следствие вытекает из неравенств
rang AB ≤ rang В (теорема 5.3),
rang AB ≥ rang В (теорема 5.4 при rang А = n).
Из этих неравенств получим, что rang AB = rang В. Аналогично доказывается соотношение rang ВА = rang В.
Теорема Кронекера-Капелли.
http://function-x.ru/systems_kroneker_kapelli.html
Теорема Кронекера-Капелли о совместности системы. Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы этой системы был равен рангу её расширенной матрицы, то есть чтобы  .
.
Здесь матрица A (матрица системы) - это матрица, составленная из коэффициентов при неизвестных:

В свою очередь матрица В (расширенная матрица) - это матрица, полученная присоединением к матрице системы столбца из свободных членов:

Ранги этих матриц связаны неравенством  , при этом ранг матрицы В может быть лишь на одну единицу больше ранга матрицы A.
, при этом ранг матрицы В может быть лишь на одну единицу больше ранга матрицы A.
Теорема о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда, если ранг матрицы равен числу неизвестных ( ), то система имеет единственное решение. Если ранг матрицы системы меньше числа неизвестных (
), то система имеет единственное решение. Если ранг матрицы системы меньше числа неизвестных ( ), то система имеет бесконечно много решений, а именно: некоторым n - r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
), то система имеет бесконечно много решений, а именно: некоторым n - r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть  , то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен m, так как ранг матрицы не может быть больше числа её строчек.
, то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен m, так как ранг матрицы не может быть больше числа её строчек.
В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:
1) отыскать в матрице системы A ранга  отличный от нуля минор
отличный от нуля минор  порядка, равного рангу матрицы системы, то есть ранга r;
порядка, равного рангу матрицы системы, то есть ранга r;
2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор  ;
;
3) члены с коэффициентами, не входящими в  , перенести в правую часть, а затем, придавая неизвестным, находящимся в правой части, произвольные значения, определить по формулам Крамера оставшиеся r неизвестных из системы r уравнений с отличным от нуля определителем
, перенести в правую часть, а затем, придавая неизвестным, находящимся в правой части, произвольные значения, определить по формулам Крамера оставшиеся r неизвестных из системы r уравнений с отличным от нуля определителем  .
.
Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор

отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному  придаём произвольное значение
придаём произвольное значение  .
.
Оставшиеся неизвестные определяются из системы
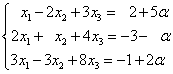
Решая последнюю систему по формулам Крамера или иным способом, находим
 ,
,
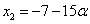 ,
,
 .
.
Присоединяя сюда  , получаем все решения данной системы линейных уравнений.
, получаем все решения данной системы линейных уравнений.
Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений

Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы:
 .
.
Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:
 .
.
Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:
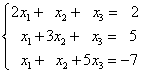
Решая последнюю систему по формулам Крамера, находим
 ,
,
 ,
,
 .
.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13
1. Образ и ядро линейного оператора в линейном пространстве.
http://www.studfiles.ru/preview/893437/page:6/
Определение:
 , тогда его ядром
, тогда его ядром 
это множество тех векторов пространства L, которые оператором A переводятся в 0.
Примеры
1) 

2) А – проектирование пространства  на плоскостиX0Y
на плоскостиX0Y


Свойства ядра:
Лемма: ядро всякого оператора – это инвариантное подпространство.
Доказательство.
1) Если  , то их линейная комбинация так же лежит в ядре. Рассмотрим
, то их линейная комбинация так же лежит в ядре. Рассмотрим 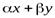

2) Образ ядра – это 0.
 ч.т.д.
ч.т.д.
Определение:
Образ – это множество всех образов, образ оператора A: ImA – это множество всех векторов из пространства L, которые могут быть записаны как образы Каши (?) либо элементов

Пример Дифферен.  образ-
образ- 
1) 

2) оператора проектирования 
Лемма:
Образ линейного оператора инвариантное подпространство.
 = инвариантное подпространство
= инвариантное подпространство
Доказательство:
1)  рассмотрим
рассмотрим 


Если 2 элемента лежат в образе, то их линейная комбинация лежит в образе.
2) Докажем, что это подпространство инвариантно.


3) Лемма: размерность ядра и образа линейного оператора.
 , dim A=n,
, dim A=n,

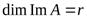
тогда n=m+r
Доказательство.
Зафиксируем какой-нибудь базис
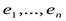 - базис
- базис 
построим матрицу оператора в этом базисе
 - матрица
- матрица 

среди векторов  ; r –ЛНЗ следовательно …
; r –ЛНЗ следовательно …
Вектора  порождают образы – это система образующих, тогда в
порождают образы – это система образующих, тогда в  - r – ЛНЗ столбцов следовательно.
- r – ЛНЗ столбцов следовательно.
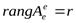
рассмотрим ядро.
2) 

 Xe =0
Xe =0
 = rang r пространство решений n-r системы размерность
= rang r пространство решений n-r системы размерность
эта размерность и есть размерность ядра m=n-r
==
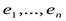 - базис каждому
- базис каждому 
y=Ax 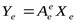
Im A тогда соответствует
 - это линейные комбинации столбцов матрицы А
- это линейные комбинации столбцов матрицы А
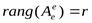
2 Решение неоднородных систем линейных уравнений. Представление общего решения в векторной форме.
http://www.cleverstudents.ru/systems/solving_systems_of_linear_equations.html
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14




 im A. Поэтому dim(im AB) ≤ dim(im A), т.е. rang AB ≤ rang А.
im A. Поэтому dim(im AB) ≤ dim(im A), т.е. rang AB ≤ rang А.  , а это может быть, в силу выбора x1,x2,...,xp, лишь при λk, = 0, к = 1, 2,..., р). Поэтому элементы Bx1,Bx2,...,Bxp принадлежат ker А, т.е. р ≤ dim (ker А). Из этого неравенства и соотношений (5.9) и (5.10) вытекает требуемое неравенство (5.8). Теорема доказана.
, а это может быть, в силу выбора x1,x2,...,xp, лишь при λk, = 0, к = 1, 2,..., р). Поэтому элементы Bx1,Bx2,...,Bxp принадлежат ker А, т.е. р ≤ dim (ker А). Из этого неравенства и соотношений (5.9) и (5.10) вытекает требуемое неравенство (5.8). Теорема доказана.  .
.

 , при этом ранг матрицы В может быть лишь на одну единицу больше ранга матрицы A.
, при этом ранг матрицы В может быть лишь на одну единицу больше ранга матрицы A. ), то система имеет единственное решение. Если ранг матрицы системы меньше числа неизвестных (
), то система имеет единственное решение. Если ранг матрицы системы меньше числа неизвестных ( ), то система имеет бесконечно много решений, а именно: некоторым n - r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
), то система имеет бесконечно много решений, а именно: некоторым n - r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом. , то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен m, так как ранг матрицы не может быть больше числа её строчек.
, то система совместна при любых свободных членах. В этом случае ранг расширенной матрицы также равен m, так как ранг матрицы не может быть больше числа её строчек. отличный от нуля минор
отличный от нуля минор  порядка, равного рангу матрицы системы, то есть ранга r;
порядка, равного рангу матрицы системы, то есть ранга r;

 придаём произвольное значение
придаём произвольное значение  .
.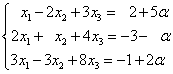
 ,
,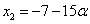 ,
, .
. , получаем все решения данной системы линейных уравнений.
, получаем все решения данной системы линейных уравнений.
 .
. .
.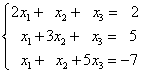
 ,
, ,
, .
. , тогда его ядром
, тогда его ядром 


 на плоскостиX0Y
на плоскостиX0Y

 , то их линейная комбинация так же лежит в ядре. Рассмотрим
, то их линейная комбинация так же лежит в ядре. Рассмотрим 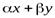

 ч.т.д.
ч.т.д.
 образ-
образ- 



 = инвариантное подпространство
= инвариантное подпространство рассмотрим
рассмотрим 





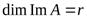
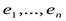 - базис
- базис 
 - матрица
- матрица 

 ; r –ЛНЗ следовательно …
; r –ЛНЗ следовательно … порождают образы – это система образующих, тогда в
порождают образы – это система образующих, тогда в 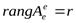


 Xe =0
Xe =0
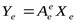
 - это линейные комбинации столбцов матрицы А
- это линейные комбинации столбцов матрицы А