Тема 7
Расчет прочности и жесткости простых балок.
Лекция №11
11.1 Касательные напряжения при изгибе.
11.2 Распределение касательных напряжений в сечениях балок различной формы.
11.3 Расчет прочности в заданном сечении двутавровой балки.
11.4 Траектории главных напряжений.
Касательные напряжения при изгибе.
В общем случае в поперечном сечении балки при плоском изгибе возникают два силовых фактора: изгибающий момент  и поперечная сила
и поперечная сила  . Изгибающий момент реализуется в поперечном сечении системой нормальных напряжений.
. Изгибающий момент реализуется в поперечном сечении системой нормальных напряжений.
Поперечная сила  , вектор которой лежит в плоскости сечения, вызывает в точках сечения касательные напряжения
, вектор которой лежит в плоскости сечения, вызывает в точках сечения касательные напряжения  (рис. 11.1, а)
(рис. 11.1, а)
Рис.11.1 Напряжения при плоском поперечном изгибе
 По закону парности касательных напряжений на продольных площадках возникают равные им касательные напряжения
По закону парности касательных напряжений на продольных площадках возникают равные им касательные напряжения  (рис 11.1,б).
(рис 11.1,б).
Таким образом, в продольном сечении возникают усилия сдвига, интенсивность которых обозначим  (усилие, приходящееся на единицу длины, Н/м, рис. 11.2, б).
(усилие, приходящееся на единицу длины, Н/м, рис. 11.2, б).

Рис. 11.2 Касательные напряжения принимаются постоянными
по ширине сечения (по оси z)
Рассмотрим равновесие отсеченной части балки (рис. 11.2, б). Равнодействующая усилий 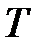 уравновешивает продольную силу
уравновешивает продольную силу  , действующую на площади
, действующую на площади  поперечного сечения. Считая справедливой формулу для нормальных напряжений
поперечного сечения. Считая справедливой формулу для нормальных напряжений 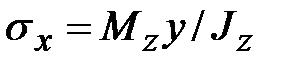 , получим
, получим
где  - статический момент относительно оси z отсеченной части сечения.
- статический момент относительно оси z отсеченной части сечения.
Интенсивность сил  изменяется по длине балки. Рассмотрим равновесие элемента балки длиной
изменяется по длине балки. Рассмотрим равновесие элемента балки длиной 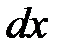 с площадью поперечного сечения
с площадью поперечного сечения  . Сумма проекций всех сил на ось x дает (см. рис 11.2, в):
. Сумма проекций всех сил на ось x дает (см. рис 11.2, в):
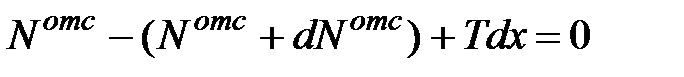 , ,
|  . .
| (11.2)
|
Сделаем допущение о том, что касательные напряжения  по ширине сечения b распределены равномерно (рис. 11.1, б). Тогда
по ширине сечения b распределены равномерно (рис. 11.1, б). Тогда
Ограничимся рассмотрением балок постоянного сечения, тогда 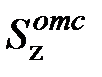
,  не зависят от координаты
не зависят от координаты  . Учитывая, что
. Учитывая, что  , получим:
, получим:

| 
| (11.4)
|
Интенсивность сдвигающих усилий  (погонная сдвигающая сила)
(погонная сдвигающая сила)
Формула (11.4) – формула Журавского.
Расчет прочности в заданном сечении двутавровой балки
В заданном сечении находят величины Q и M. В масштабе вычерчивают идеализированный двутавр, представляющий собой совокупность прямоугольных элементов – полок шириной b и толщиной t и стенки высотой (h–2t) и толщиной s (Рис 11.8).
Вычисление напряжений.
В точках 1,3,4,5,7, взятых через одну четверть высоты балки, и в местах сопряжения стенки с полками (точки 2,6) вычисляют нормальные и касательные напряжения по формулам
 , (10)
, (10)
где y– ордината рассматриваемой точки;  – ширина сечения;
– ширина сечения;  – статический момент отсеченной части сечения (для точек 1,7:
– статический момент отсеченной части сечения (для точек 1,7:  , для точек 2¸6:
, для точек 2¸6: 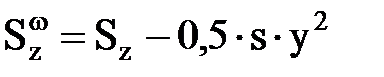 и b = s).
и b = s). 
Эпюры s и t строят в масштабе справа от идеализированного двутавра с указанием значений в рассмотренных выше точках. Эпюру t строят только в пределах стенки. На эпюрах проставляют знаки нормальных напряжений и указывают направление касательных напряжений (положительных – вниз, отрицательных – вверх).
Тема 7
Расчет прочности и жесткости простых балок.
Лекция №11
11.1 Касательные напряжения при изгибе.
11.2 Распределение касательных напряжений в сечениях балок различной формы.
11.3 Расчет прочности в заданном сечении двутавровой балки.
11.4 Траектории главных напряжений.



 и поперечная сила
и поперечная сила  . Изгибающий момент реализуется в поперечном сечении системой нормальных напряжений.
. Изгибающий момент реализуется в поперечном сечении системой нормальных напряжений. , вектор которой лежит в плоскости сечения, вызывает в точках сечения касательные напряжения
, вектор которой лежит в плоскости сечения, вызывает в точках сечения касательные напряжения  (рис. 11.1, а)
(рис. 11.1, а)

 По закону парности касательных напряжений на продольных площадках возникают равные им касательные напряжения
По закону парности касательных напряжений на продольных площадках возникают равные им касательные напряжения  (рис 11.1,б).
(рис 11.1,б). (усилие, приходящееся на единицу длины, Н/м, рис. 11.2, б).
(усилие, приходящееся на единицу длины, Н/м, рис. 11.2, б).
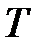 уравновешивает продольную силу
уравновешивает продольную силу  , действующую на площади
, действующую на площади  поперечного сечения. Считая справедливой формулу для нормальных напряжений
поперечного сечения. Считая справедливой формулу для нормальных напряжений 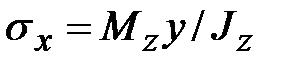 , получим
, получим



 - статический момент относительно оси z отсеченной части сечения.
- статический момент относительно оси z отсеченной части сечения. изменяется по длине балки. Рассмотрим равновесие элемента балки длиной
изменяется по длине балки. Рассмотрим равновесие элемента балки длиной 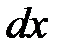 с площадью поперечного сечения
с площадью поперечного сечения 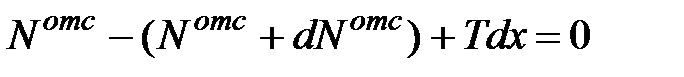 ,
,
 .
.
 по ширине сечения b распределены равномерно (рис. 11.1, б). Тогда
по ширине сечения b распределены равномерно (рис. 11.1, б). Тогда ,
,
 ,
,

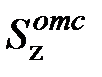
 не зависят от координаты
не зависят от координаты  . Учитывая, что
. Учитывая, что  , получим:
, получим:

 (погонная сдвигающая сила)
(погонная сдвигающая сила)

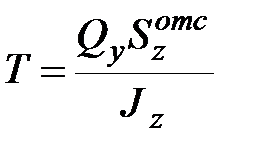
 , (10)
, (10) – ширина сечения;
– ширина сечения;  – статический момент отсеченной части сечения (для точек 1,7:
– статический момент отсеченной части сечения (для точек 1,7:  , для точек 2¸6:
, для точек 2¸6: 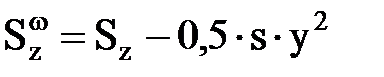 и b = s).
и b = s). 


