Внутренние силы – приращение сил взаимодействия между частицами тела, возникающих при его нагружении.

Рис. 2.6 Нормальные и касательные напряжения в точке
Тело рассечено плоскостью (рис.2.6 а) и в этом сечении в рассматриваемой точке М выделена малая площадка  , её ориентация в пространстве определяется нормалью n. Равнодействующую силу на площадке
, её ориентация в пространстве определяется нормалью n. Равнодействующую силу на площадке  обозначим через
обозначим через  . Среднюю интенсивность на площадке определим по формуле
. Среднюю интенсивность на площадке определим по формуле  . Интенсивность внутренних сил в точке определим как предел
. Интенсивность внутренних сил в точке определим как предел
 (2.1)
(2.1) 
Интенсивность внутренних сил  передающихся в точке через выделенную площадку, называется напряжением на данной площадке.
передающихся в точке через выделенную площадку, называется напряжением на данной площадке.
Размерность напряжения  .
.
Вектор  определяет полное напряжение на данной площадке. Разложим его на составляющие (рис.2.6 б) так, что
определяет полное напряжение на данной площадке. Разложим его на составляющие (рис.2.6 б) так, что  , где
, где 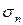 и
и  – соответственно нормальное и касательное напряжения на площадке с нормалью n.
– соответственно нормальное и касательное напряжения на площадке с нормалью n.
При анализе напряжений в окрестности рассматриваемой точки М (рис.2.6 в) выделяют бесконечно малый элемент в форме параллелепипеда со сторонами  ,
,  ,
, 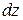 (проводят 6 - сечений). Полные напряжения, действующие на его гранях, раскладывают на нормальное и два касательных напряжения. Совокупность напряжений, действующих на гранях, представляют в виде матрицы (таблицы), которую называют тензор напряжений
(проводят 6 - сечений). Полные напряжения, действующие на его гранях, раскладывают на нормальное и два касательных напряжения. Совокупность напряжений, действующих на гранях, представляют в виде матрицы (таблицы), которую называют тензор напряжений
 (2.2)
(2.2)
Первый индекс у напряжения, например 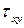 , показывает, что оно действует на площадке с нормалью, параллельной оси
, показывает, что оно действует на площадке с нормалью, параллельной оси  , а второй показывает, что вектор напряжений параллелен оси у. У нормального напряжения оба индекса совпадают поэтому ставится один индекс.
, а второй показывает, что вектор напряжений параллелен оси у. У нормального напряжения оба индекса совпадают поэтому ставится один индекс.
Силовые факторы в поперечном сечении стержня и их выражение через напряжения.
Рассмотрим поперечное сечение стержня нагруженного стержня (рис 2.7,а). Внутренние силы, распределенные по сечению, приведем к главному вектору R, приложенному в центре тяжести сечения, и главному моменту M. Далее разложим их на шесть компонент: три силы 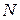 ,
,  ,
,  и три момента
и три момента  ,
, 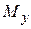 ,
,  , называемые внутренними усилиями в поперечном сечении.
, называемые внутренними усилиями в поперечном сечении.


Рис. 2.7 Внутренние усилия и напряжения в поперечном сечении стержня.
Компоненты главного вектора и главного момента внутренних сил, распределенных по сечению, называются внутренними усилиями в сечении ( 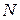 - продольная сила;
- продольная сила;  ,
,  - поперечные силы,
- поперечные силы, 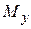 ,
,  - изгибающие моменты,
- изгибающие моменты,  - крутящий момент).
- крутящий момент).
Выразим внутренние усилия через напряжения, действующие в поперечном сечении, предполагая их известными в каждой точке (рис. 2.7,б)
Выражение внутренних усилий через напряжени я.





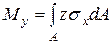
 (2.3)
(2.3)
Метод сечений
При действии на тело внешних сил оно деформируется. Следовательно, меняется взаимное расположение частиц тела; в результате этого возникают дополнительные силы взаимодействия между частицами. Эти силы взаимодействия в деформированном теле есть внутренние усилия. Необходимо уметь определять значения и направления внутренних усилий через внешние силы, действующие на тело. Для этого используется метод сечений.

Рис. 2.8 Определение внутренних усилий методом сечений.
Уравнения равновесия для оставшейся части стержня.
 ,
,  ,
, 
 ,
,  ,
,  (2.4)
(2.4)
Из уравнений равновесия определяем внутренние усилия в сечении a-a.
Перемещения и деформации.
Под действием внешних сил тело деформируется, т.е. изменяет свои размеры и форму (рис.2.9). Некоторая произвольная точка M переходит в новое положение M1. Полное перемещение MM1 будем разлагать на компоненты u, v, w, параллельные осям координат.
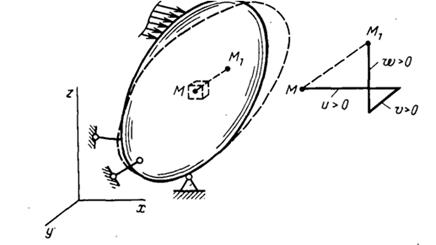
Рис 2.9 Полное перемещение точки и его компоненты.
Но перемещение данной точки еще не характеризует степень деформирования элемента материала у этой точки ( пример: человек висит на канате, часть каната ниже захвата не деформируется).
Введем понятие деформаций в точке как количественную меру деформирования материала в её окрестности. Выделим в окрестности т. М элементарный параллелепипед  (рис. 2.10). За счет деформации длины его ребер получат удлинение
(рис. 2.10). За счет деформации длины его ребер получат удлинение  .
.

Рис 2.10 Линейная и угловая деформации элемента материала.
Линейные относительные деформации в точке определятся так ( ):
):
Кроме линейных деформаций возникают угловые деформации или углы сдвига, представляющие малые изменения первоначально прямых углов параллелепипеда (например, в плоскости  это будет
это будет  ). Углы сдвига весьма малы и имеют порядок
). Углы сдвига весьма малы и имеют порядок 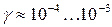 .
.
Введенные относительные деформации в точке сведем в матрицу
 . (2.6)
. (2.6)
Величины (2.6) количественно определяют деформацию материала в окрестности точки и составляют тензор деформаций.
Принцип суперпозиции.
Систему, в которой внутренние усилия, напряжения, деформации и перемещения прямо пропорциональны действующей нагрузке, называют линейно деформируемой (материал работает как линейно-упругий).
Кроме того, перемещения в конструкции должны быть достаточно малыми, чтобы изменения ее размеров и формы, возникающие вследствие деформации, можно было не учитывать в расчетной схеме (при составлении уравнений равновесия). Такие системы называются геометрически линейными.

Рис.2.11 Влияние перемещения узла на усилие в стержне
На рис.2.11 показана геометрически нелинейная система  . Если пренебречь деформацией стержней и считать
. Если пренебречь деформацией стержней и считать 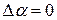 , то
, то 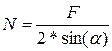 .
.
Принцип суперпозиции. Результат действия группы сил равен сумме (алгебраической или геометрической) результатов, полученных от действия каждой силы в отдельности.




 , её ориентация в пространстве определяется нормалью n. Равнодействующую силу на площадке
, её ориентация в пространстве определяется нормалью n. Равнодействующую силу на площадке  обозначим через
обозначим через  . Среднюю интенсивность на площадке определим по формуле
. Среднюю интенсивность на площадке определим по формуле  . Интенсивность внутренних сил в точке определим как предел
. Интенсивность внутренних сил в точке определим как предел (2.1)
(2.1) 
 передающихся в точке через выделенную площадку, называется напряжением на данной площадке.
передающихся в точке через выделенную площадку, называется напряжением на данной площадке. .
. определяет полное напряжение на данной площадке. Разложим его на составляющие (рис.2.6 б) так, что
определяет полное напряжение на данной площадке. Разложим его на составляющие (рис.2.6 б) так, что  , где
, где 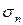 и
и  – соответственно нормальное и касательное напряжения на площадке с нормалью n.
– соответственно нормальное и касательное напряжения на площадке с нормалью n. ,
,  ,
, 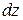 (проводят 6 - сечений). Полные напряжения, действующие на его гранях, раскладывают на нормальное и два касательных напряжения. Совокупность напряжений, действующих на гранях, представляют в виде матрицы (таблицы), которую называют тензор напряжений
(проводят 6 - сечений). Полные напряжения, действующие на его гранях, раскладывают на нормальное и два касательных напряжения. Совокупность напряжений, действующих на гранях, представляют в виде матрицы (таблицы), которую называют тензор напряжений (2.2)
(2.2) 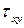 , показывает, что оно действует на площадке с нормалью, параллельной оси
, показывает, что оно действует на площадке с нормалью, параллельной оси  , а второй показывает, что вектор напряжений параллелен оси у. У нормального напряжения оба индекса совпадают поэтому ставится один индекс.
, а второй показывает, что вектор напряжений параллелен оси у. У нормального напряжения оба индекса совпадают поэтому ставится один индекс.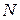 ,
,  ,
,  и три момента
и три момента  ,
, 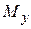 ,
,  , называемые внутренними усилиями в поперечном сечении.
, называемые внутренними усилиями в поперечном сечении.





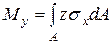
 (2.3)
(2.3)
 ,
,  ,
, 
 ,
,  ,
,  (2.4)
(2.4)
 (рис. 2.10). За счет деформации длины его ребер получат удлинение
(рис. 2.10). За счет деформации длины его ребер получат удлинение  .
.
 ):
):
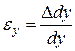

 это будет
это будет  ). Углы сдвига весьма малы и имеют порядок
). Углы сдвига весьма малы и имеют порядок 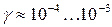 .
. . (2.6)
. (2.6)
 . Если пренебречь деформацией стержней и считать
. Если пренебречь деформацией стержней и считать 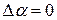 , то
, то 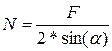 .
.


