Основы графической визуализации вычислений

Построение графика функций одной переменной

Функции одной переменной у(х) находят широкое применение в практике математических расчетов и технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой системе координат. Как и другие системы компьютерной математики, MATLAB строит графики функций по ряду точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками.

Для построения графиков функций в декартовой системе координат служит команда plot. Например, вызов функции plot (X, Y) приведет к построению графика функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то будет построено семейство графиков по данным, содержащимся в колонках матрицы.

В качестве примера построения графика функций одной переменной рассмотрим построение синусоиды. Для построения заданного графика используем команду plot(sin(x)), предварительно задав интервал изменения аргумента с помощью вектора х=0:0.1:10. Результат построения графика будет выведен в отдельном масштабируемом и перемещаемом графическом окне (рис. 4.10).

 

Рис. 4.10. Построение графика синусоиды.

В одном графическом окне можно одновременно построить графики сразу нескольких функций. Например, можно задать переменные y1=sin(x); y2=cos(x);, а затем вызвать команду plot(x,y1,x,y2). Результат построения можно увидеть на рис. 4.11.

Рис. 4.11. Пример построения в одном графическом окне графиков двух функций.

Команда plot(X,Y,S) — аналогична команде plot(X,Y), но с помощью третьего параметра, строковой константы S, она дает возможность задавать тип линии графика. Значения константы S приведены в таблице 4.5.

 

Таблица 4.5. Значения параметра S команды plot(X,Y,S).

 

Цвет линии		Тип маркера
Y	Желтый	.	Точка
М	Фиолетовый		Окружность
С	Голубой	X	Крест
R	Красный	+	Плюс
G	Зеленый	*	Звездочка
В	Синий	S	Квадрат
W	Белый	D	Ромб
К	Черный	V	Треугольник (вниз)
		А	Треугольник (вверх)
		<	Треугольник (влево)
		>	Треугольник (вправо)
		Р	Пятиугольник
Тип линии
–	Сплошная
;	Двойной пунктир
–.	Штрих-пунктир
– –	Штриховая

 

Рассмотрим пример построения графиков трех функций с различным стилем представления каждой из них. Сначала зададим интервал изменения аргумента и сами функции y1, y2, и y3, а затем применим команду plot(x, yl,'- m',x, y2,'-. + r',x,y3,'- - o k'), как это представлено на рис. 4.12.

 

Рис. 4.12. Пример применения команды plot(X,Y,S).

Результат построения продемонстрирован на рис. 4.13.

 

Рис. 4.13. Пример построения графиков трех функций с различным стилем представления каждой из них.

 

Для построения графиков функций со значениями х и у, изменяющимися в широких пределах, как правило, используются логарифмические масштабы для координатных осей X и У. Для построения графика в этом случае используется команда loglogx(), синтаксис которой аналогичен ранее рассмотренному для функции plot(). Логарифмический масштаб используется. Ниже дан пример применения данной команды:

 

>>x=logspace(-1,3);

>>loglog(x, exp(x)./x)

>>grid on

Обратите внимание на то, что командой grid on строится координатная сетка. На рис. 4.14 представлен график функции ехр(х)/х в логарифмическом масштабе, о чем свидетельствует неравномерное расположение линий координатной сетки.

 

Рис. 4.14. График функции ехр(x)/x в логарифмическом масштабе.

В некоторых случаях предпочтителен полулогарифмический масштаб графиков, когда по одной оси задается логарифмический масштаб, а по другой — линейный. Для построения графиков функций в подобных случаях используются следующие команды:

· semilogx() — строит график функции в логарифмическом масштабе (основание 10) по оси X и линейном по оси Y;

· semilоgу () — строит график функции в логарифмическом масштабе по оси Y и линейном по оси X.

Запись параметров для представленных функций выполняется по аналогии с функцией plot().

Построение графика линии на плоскости в полярной системе координат осуществляется с помощью функции polar (phi, rho, s), где phi – задает полярный угол в радианах, rho – полярный радиус, а необязательный аргумент s служит для задания свойств линии и маркеров. Например, последовательный вызов приведенных ниже команд сформирует графическое окно представленное на рис. 4.15.

 

>> t=0:pi/50:2*pi;

>> polar(t,sin(5*t))

Рис. 4.15. Пример построения графика в полярной системе координат.

 

В прикладных расчетах часто встречаются графики, именуемые столбцовыми диаграммами, отражающие содержание некоторого вектора V. Особенно часто этот тип диаграмм используются при представлении данных финансово-экономических расчетов. При этом каждый элемент вектора представляется столбцом, высота которого пропорциональна значению элемента. Столбцы нумеруются и масштабируются по отношению к максимальному значению наиболее высокого столбца. Выполняет построение такого графика одна из следующих команд:

bar(x, Y) — строит столбцовый график элементов вектора Y (или группы столбцов для матрицы Y) со спецификацией положения столбцов, заданной значениями элементов вектора х, которые должны идти в монотонно возрастающем порядке;

bar(Y) — строит график значений элементов матрицы Y, а в качестве х используется вектор х=1:m;

BAR(Y,WIDTH) — команда аналогична ранее рассмотренным, но со спецификацией ширины столбцов (при WIDTH > 1 столбцы в одной и той же позиции перекрываются). По умолчанию задано WIDTH = 0.8.

По аналогии с командой plot в приведенных командах построения столбцовых диаграмм возможно задание спецификаций графиков, например типа линий, цвета и т. д. Спецификация 'stacked' задает рисование всех n столбцов в позиции m друг на друге, как это представлено на рис. 4.16. Помимо команды bar() существует аналогичная ей по синтаксису команда barh(), которая" строит столбцовые диаграммы с горизонтальным расположением столбцов.

 

Рис. 4.16. Пример построения диаграммы с вертикальными столбцами

 

Закрашенные секторы часто используются для построения цветных плоских круговых диаграмм. Для их построения в MATLAB служит команда piе:

pie(X) — строит круговую диаграмму по данным нормализованного вектора X/ SUM(X). При этом, если SUM(X)<=1.0, то значения в X непосредственно определяют площадь секторов;

pie(X,EXPLODE) — строит круговую диаграмму, у которой отрыв секторов от центра задается вектором EXPLODE, который должен иметь тот же размер, что и вектор данных X.

Система MATLAB также предоставляет возможность построения объемных круговых диаграмм с помощью команды pie3(), аналогичной команде pie(). На рис. 4.17 демонстрируется пример построения двух видов круговых диаграмм: плоской и объемной. В качестве исходных данных в обоих случаях берется вектор Х=[1 2 3 4 5]. Для построения плоской диаграммы используется команда pie(X,[1 1 1 1 1]), а для объемной – pie3(X,[1 1 1 1 1]).

 

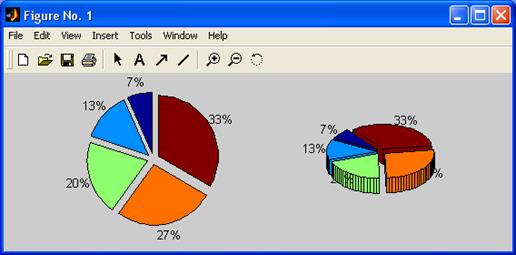
Рис. 4.17. Пример построения круговых диаграмм.

В системе MATLAB предусмотрена также возможность построения графиков в полярной системе координат. Напомним, что в данной системе координат любая точка представляется как конец радиус-вектора, исходящего из начала системы координат под углом ТНЕТА к горизонтали и имеющего длину R. Для построения графика в этом случае используется команда polar(THETA,R, S), где параметр THETA обычно меняется от 0 до 2*pi, а строковая константа S, задающая стиль построения, не является обязательным параметром.

Команда plot3(X,Y,Z,S) является аналогом команды plot (), но относится к функции двух переменных z(x, у). Она строит аксонометрическое изображение трехмерных поверхностей, определяемых матрицами одинакового размера X, Y и Z. Совместно с функциями построения графиков трехмерных поверхностей обычно используется функция meshgrid, формирующая двумерные массивы X и Y. Например, для преобразования области, заданной векторами х и у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков, можно воспользоваться выражением [X, Y] = meshgrid(x, y). При этом, строки выходного массива X будут являться копиями вектора х; а столбцы Y — копиями вектора у (рис. 4.18).

 

Рис. 4.18. Пример использования функции meshgrid().

 

Рассмотрим пример построения трехмерной поверхности, описываемой функцией . Листинг необходимый для построения команд приведен на рис. 4.19.

Рис. 4.19. Построение поверхности, описываемой функцией .

 

Результат построения демонстрируется на рис. 4.20.

 

Рис. 4.20. График поверхности, построенный линиями.

 

Наиболее представительными и наглядными являются сетчатые графики поверхностей с заданной или функциональной окраской. Для их построения предназначена функция mesh(X,Y,Z,C), которая выводит в графическое окно сетчатую поверхность Z(X.Y) с цветами узлов поверхности, заданными массивом С. При этом параметр C не является обязательным, то есть допустим вызов команды mesh(X,Y,Z). В этом случае C=Z и используется функциональная окраска, при которой цвет задается высотой поверхности. Пример построения сетчатого графика поверхности, описываемой функцией , с использованием функциональной окраски представлен на рис. 4.21.

Рис. 4. 21. Сетчатый график поверхности с функциональной окраской.

При использовании функциональной окраски весьма полезным является вывод шкалы цветов командой colorbar. Ее варианты перечислены ниже:

colorbar('vert') — выводит вертикальную шкалу цветов на текущий график (см. рис. 4.21);

colorbar('horiz') — выводит горизонтальную шкалу цветов на текущий график;

colorbar — устанавливает в текущий график новую вертикальную шкалу цветов или обновляет уже имеющуюся.

 

Иногда график поверхности полезно объединить с контурным графиком ее проекции на плоскость, расположенным под поверхностью. Для этого используется команда meshc(), аналогичная команде mesh(), но помимо графика поверхности строящая изображение ее проекции в виде линий равного уровня, что дает наилучшее представление об особенностях поверхности.

После того как график уже построен, MATLAB позволяет выполнить его форматирование в нужном виде. Для форматирования графиков в системе предназначены команды Figure Properties (Свойства рисунка), Axis Properties (Свойства осей) и Current ObjectProperties (Свойства текущего объекта) меню Edit графического окна. С помощью перечисленных команд можно, например, отформатировать линию графика, установив стиль отображения линии (сплошная, пунктирная и т.д.), ее ширину, цвет, а также параметры маркеров, отмечающих опорные точки графиков. Эти точки появляются на графике, если в поле свойств маркера Marker Properties (Свойства маркера) вкладки Style (Стиль) диалогового окна форматирования выбрать стиль маркера. При этом маркеры можно задавать в виде окружностей, прямоугольников, крестиков, ромбиков и т. д. Кроме того, здесь же можно задавать их размеры, цвет их закраски и цвет окантовки.

Команда Axis Properties меню Edit графического окна позволяет отформатировать оси графиков. Например, можно задать линейный или логарифмический масштаб осей (поле Scale (Масштаб)), нормальное или инверсное направление осей(X, У, а в случае трехмерных графиков и Z), показ сетки (параметр Grid Show), изменить стиль осей и цвет фона, нанести у осей надписи (поле Label (Ярлык)) и пр.

Дополнительно на график можно нанести надписи с помощью команды Text меню Insert или кнопки панели инструментов . Место надписи фиксируется щелчком мыши. Полученную таким образом надпись можно выделить и перенести мышью в любое другое место. Кроме того, контекстное меню надписи позволяет отформатировать текст надписи, выбрав стиль, размер и цвет символов. Помимо этого на график можно нанести стрелки (кнопка ) и линии без стрелки (кнопка ).

Режим редактирование графиков включается командой Edit Plot (Редактировать график) меню Tools (Инструменты). С помощью команд этого меню можно, например, увеличить (команда Zoom In) или уменьшить (команда Zoom Out) размеры графика или можно начать его поворот мышью (команда Rotate 3D).

Команды меню Insert (Вставка) дают возможность нанесения надписей по осям, титульной надписи, надписи внутри рисунка, стрелки, отрезка прямой, легенды и шкалы цветов. Команда Legend (Легенда) рассматриваемого меню подключает к графику легенду — пояснение в виде отрезков линий со справочными надписями, размещаемое внутри графика или около него. Каждая линия легенды имеет тот же цвет и стиль, что и на графике.

Обычно график занимает фиксированное положение в центре графического окна. Однако в режиме редактирования графиков в контекстном меню области графика доступна команда Unlock Axes Position (Отключить позиционирование осей). Она снимает фиксацию положения координатных осей графика и позволяет двигать его мышью вместе с осями. При этом перемещение графика не влияет на размещение его легенды и цветовой диаграммы, которые остаются на прежнем месте.

Бывает, что в одном окне надо расположить несколько координатных осей с различными графиками без наложения их друг на друга. Для этого используются команды subplot, применяемые перед построением графиков:

subplot(m, n, p) – разбивает графическое окно на m x n подокон, при этом m — число подокон по горизонтали, n — число подокон по вертикали, а р — номер подокна, в которое будет выводиться текущий график (подокна отсчитываются последовательно по строкам);

subplot('position',[left bottom width height]) — создает подокно с заданными нормализованными координатами (в пределах от 0.0 до 1.0).
Например, последовательный вызов приведенных ниже команд сформирует графическое окно представленное на рис. 4.22.

 

>>X1= -5: 0.1: 5;

>>subplot(2,2,1), plot(sin(x))

>>subplot(2,2,2), plot(sin(5*X1),cos(2*X1+0.2))

>> [X,Y]=meshgrid([-3:0.15:3]);

>>Z=X.^2+Y.^2;

>>subplot(2,2,3), plot3(X,Y,Z)

>>subplot(2,2,4), mesh(X,Y,Z)

Рис. 4.22. Пример разбиения графического окна на подокна.

 

Следует отметить, что для всех графиков возможна индивидуальная установка дополнительных объектов, например титульных надписей, надписей по осям и т. д.

 

Установка палитры цветов

Графика MATLAB обеспечивает не только получение цветных изображений, но и управление цветом и различными световыми эффектами. Среди них важное место занимает установка палитры цветов. Палитра цветов RGB задается матрицей MAP из трех столбцов, определяющих значения интенсивности красного (red), зеленого (green) и синего (blue) цветов. Их интенсивность задается в относительных единицах от 0.0 до 1.0. При изменении интенсивности цветов в указанных пределах возможно задание любого цвета. Так, например, [0 0 0] задает черный цвет, [1 1 1] — белый цвет, [1 0 0] — красный цвет.

Для установки палитры цветов служит команда colormap, записываемая в следующих формах:

· colormap('default') — устанавливает палитру по умолчанию, при которой распределение цветов соответствует радуге;

· colormap(MAP) — устанавливает палитру RGB, заданную матрицей MAP;

· C=colormap — функция возвращает матрицу текущей палитры цветов С.

Приведем несколько характерных палитр, которые могут служить параметрами команды colormap:

· hsv — цвета радуги;

· hot — чередование черного, красного, желтого и белого цветов;

· gray — линейная палитра в оттенках серого цвета;

· bone — серые цвета с оттенком синего;

· copper — линейная палитра с оттенками меди;

· pink — розовые цвета с оттенками пастели;

· white — палитра белого цвета;

· flag — чередование красного, белого, синего и черного цветов;

· lines — палитра с чередованием цветов линий;

· colorcube — расширенная палитра RGB;

· jet — разновидность палитры HSV;

· prism — призматическая палитра цветов;

· cool — оттенки голубого и фиолетового цветов;

· autumn — оттенки красного и желтого цветов;

· spring — оттенки желтого и фиолетового цветов;

· winter — оттенки синего и зеленого цветов;

· summer — оттенки зеленого и желтого цветов.

 

4.2. Практическое задание 1

Протабулируйте заданную функцию y = f(x) на промежутке [a, b ] с постоянным шагом h и постройте ее график. Отформатируйте с помощью редактора свойств линию графика, задав произвольным образом ее цвет, тип, а также тип маркера.

ВАРИАНТЫ

№	[a,b]	h	Функция
	[0;4]	0,1
	[-3;3]	0,15
	[-4;2]	0,15
	[-3;3]	0,15
	[-2;4]	0,15
	[-2;4]	0,15
	[-1;4]	0,1
	[-3;2]	0,1
	[-3;4]	0,2
	[-1;5]	0,15
	[-4;2]	0,15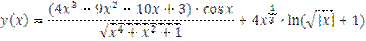
	[-2;3]	0,1

4.3. Практическое задание 2

Создайте две координатные плоскости. В нечетных вариантах плоскости располагаются вертикально, в четных – горизонтально. В первой плоскости определите прямоугольную систему координат, во второй – полярную. Постройте заданную линию в двух системах координат. В строке заголовка графического окна уберите его номер (снимите флажок Figure number в диалоговом окне Property Editor – Figure, вызываемом командой Edit → Figure Properties графического окна) и выведите номер варианта и название заданной линии (строка Window name того же диалогового окна). Исследуйте влияние значений переменных, входящих в уравнение линии, на ее вид.

При выполнении задания потребуется преобразование полярных координат в декартовы и наоборот. Выполняются указанные преобразования с помощью следующих аналитических зависимостей:

ВАРИАНТЫ

 

№ вар-та	Задание
	Построить лемнискату Бернулли, параметрические уравнения которой имеют вид:
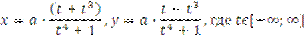
	Построить четырехлепестковую розу, заданную уравнением в полярных координатах:
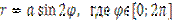
	Построить улитку Паскаля, уравнение которой в полярной системе координат имеет вид:
	Построить полукубическую параболу (параболу Нейля), параметрические уравнения которой:
	Построить спираль Архимеда, уравнения которой в полярных координатах:
	Построить конхоиду Никомеда, уравнения которой в полярных координатах:
	Построить инволюту окружности, уравнения которой в прямоугольных координатах:
	Построить кохлеоиду, уравнение которой в полярных координатах:
	Построить локон Аньези. Уравнение в прямоугольных координатах:
	Построить логарифмическую спираль, уравнение которой в полярных координатах:
	Построить гиперболическую спираль, заданную уравнением в полярных координатах:
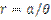
	Построить трактрису, заданную с помощью параметрических уравнений:

4.4. Практическое задание 3

 

Постройте сетчатый график заданной в варианте поверхности z=f(x,y) в прямоугольной области D: {a≤x≤b; c≤y≤d}. Для задания цвета узлов поверхности используйте функциональную окраску. Для наглядности выведите на график вертикальную шкалу цветов.

ВАРИАНТЫ

№ вар-та	Функция z=f(x,y)	[a;b]	[c;d]	Примечание
		[-3;3]	[-3;3]
		[ ]	[ ]
		[0;π]	[0;π]
		[-1;1]	[-3;0]
		[-1;1]	[-1;1]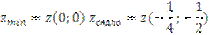
		[ ]	[ ]
		[0.1;2]	[1;3]
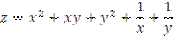
		[0.1;1]	[0.1;2]
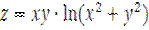
		[0.1;2]	[0.1;2]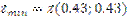
		[ ]	[ ]
		[0;2]	[-3;0]
		[0.1;2]	[0.1;2]

4.5. Контрольные вопросы.

1. Какова история создания системы MATLAB?
2. Почему MATLAB интегрированная система?
3. Что такое m-файлы и для чего их используют в системе MATLAB?
4. Что такое векторизация и что она обеспечивает?
5. Почему система MATLAB называется интегрированной?
6. Каково основное достоинство системы MATLAB по сравнению с MathСad?
7. Из каких инструментальных средств состоит Рабочий стол системы MATLAB?
8. Что записывается в файлы формата.mat?
9. Какие форматы числовых данных используются в системе MATLAB?
10. Для чего предназначен Workspace Browser?
11. Для чего используется функция clear?
12. Для чего предназначен Current Directory Browser?
13. Какие арифметические функции и операторы имеются в системе MATLAB?
14. Какие тригонометрические функции имеются в системе MATLAB?
15. Какие математические функции имеются в системе MATLAB?
16. Какие логические функции и операторы имеются в системе MATLAB?
17. Какая команда используется для построения графиков функций в декартовой системе координат?
18. Какая команда используется для построения графиков функций в логарифмическом масштабе для координатных осей X и У?
19. С помощью какой функции осуществляется построение графика линии на плоскости в полярной системе координат?
20. С помощью какой функции строится аксонометрическое изображение трехмерных поверхностей?

21. Что делает функция logspace(a.b)?

 

 

Лабораторная работа № 6