Общая структура универсального пакета

Рисунок 3 – Примеры представления результатов гидродинамических расчетов

 

Оценка уровня шума, который будет производить изделие во время эксплуатации особенно важна для автомобилестроения и в гражданской авиации. Например, шум авиадвигателей явля­ется одним из основных критери­ев качества гражданского самолета, поскольку самолеты с высоким уровнем шума аэропорты ряда стран просто не прини­мают.

К задачам акустического анализа относится определение параметров акустического поля (интенсивность, спектральный состав звука) в выбранном объеме. В качестве исходных данных необходима геометрия исследуемого пространства, спектральная характеристика и мощность источника звука. В качестве примеров модулей MSC.Software, помогающих решать акустические задачи, можно назвать Actran, Akusmod.

Линейные конечные элементы

Для конечно-элементного моделирования используются, как правило, линейные, плоские и объемные (твердотельные) элементы. В одной и той же модели в универсальных пакетах могут присутствовать все типы конечных элементов.

Линейные конечные элементы (КЭ) представляют собой линию (прямую или кривую), соединяющие два узла. При механических расчетах наиболее распространены следующие виды линейных конечных элементов:

– стержень(rod); этот КЭ работает только на растяжение и кручение. Может иметь произвольную (задаваемую пользователем или выбираемую из базы) форму поперечного сечения. Обычно используется при моделировании тросов, растяжек, подвесов и т.д.;

– балка(beam); этот КЭ работает на растяжение, изгиб, кручение. Позволяет задавать линейно по длине изменяющуюся размеры сечения, как стандартные (шестигранная труба, Z-образ­ный профиль, тавр и т.д.), так и определяемую пользова­телем. Элемент также поз­воляет проводить расчет балок с учетом искривления тонкостенных сечений при стесненном кручении и поперечном изгибе.

– пружина(spring) представляет собой невесомый линейный элемент, обладающий жесткостью ли­бо на растяжение, либо на кручение. Упругие свойства этого КЭ не зависят от его длины. Такой элемент может также моделировать явление вязкого демпфирования, соответственно, при растяжении или кручении;

– зазор (gap) предназначен для моделирования зазоров или на­тягов между элементами конструкции. Он представляет собой пружину со ступенчато изменяющейся жесткостью, например, G1 или G2. При определении параметров зазора задается значение начального зазора e₀. Если деформация при нагружении меньше e₀, то дейс­твует первое значение жесткости G1 (например, ноль). Если больше – то второе, G2. На растяжение и сжатие элемент работает одинаково. Помимо главного свойства – ступен­чатой жесткости, этот линейный элемент позволяет задавать поперечную жесткость и ко­эффициенты трения раздельно вдоль осей координат.

Кроме описанных, в некоторых видах расчетов используются дополнительные типы конечных элементов, такие как:

– масса (mass) – позволяет задавать массы и моменты инерции в выбранных узлах. Используется для описания элементов исследуемой системы, жесткостью которых в данном исследовании можно пренебречь, а вот массу и момент инерции необходимо учесть при динамических расчетах. Например, слой снега на крыше практически не влияет на ее жесткость, но существенно увеличивает ее эффективную массу;

– жесткий элемент (rigid) – позволяет создавать абсолютно жесткие связи между двумя или несколькими узлами. Удобен для задания распределенной нагрузки, а также для стыковки конечных элементов разного типа (например, пластины и стержня или пластины и твердого тела);

– линия скольжения (slide line) – предназначена для моделирования линии контакта деформируемых тел при их относительном скольжении. Позволяет моделировать зону контакта тел, задавать статический и динамический коэффициенты трения между телами.

 

10. Плоские и объемные конечные элементы

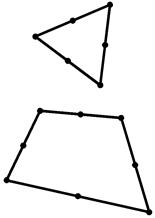
Плоские элементы предназначены для моделирования пластин, оболочек и других видов тонкостенных конструкций. Обычно используются трех- и четырехугольные плоские элементы с узлами при вершинах (рисунок 4.2.6, а), а также элементы повышенной точности (т.н. параболические элементы) с промежуточными узлами на их сторонах (показаны точками на рисунке 4.2.6, б).

 

а)	б)

Рисунок 4.2.6 – Плоские конечные элементы

 

Чаще всего используются следующие разновидности плоских конечных элементов:

– пластина(plate); этот плоский элемент позволяет при нагружении учесть все внутренние силовые факторы: мембранные, сдвиговые, поперечные и изгибные при относительно небольших затратах вычислительных ресурсов. В NASRTAN’е и ANSYS’е определен как элемент по умолчанию. Главная геометрической характеристикой пластины является толщина. При желании толщина пластины может быть задана разной на разным ее сторонах. В этом случае с точки зрения расчета она имитирует клин или призму. Такой подход бывает необходим при моделирования сложной 3D-геометрии плоскими конечными элементами (пластинами). Позволяет также задавать ребра или накладки из заданного материала, имитируя таким образом сложную геометрию.

Интересной разновидностью пластины является многослойная пластина (laminate). Она подобна обычной пластине, но может содержать до 90 слоев разной толщины, выполненных из разных материалов. Такой элемент удобно использовать при моделировании слоистых композитов.

Для моделирования тонких упругих пластин (в случае, когда толщина пластины многократно меньше радиусов ее изгиба) предназначена еще одна разновидность пластины – мембрана (membrane). В отличие от пластины, этот элемент воспринимает только нормальную нагрузку в своей плоскости, зато требует еще меньше ресурсов для расчета.

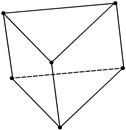
Использование линейных или пластинчатых элементов часто позволяет на порядок сократить время расчета, но наиболее универсальными являются твердотельные или объемные конечные элементы. К объемным конечным элементам относится твердотельный пространственный элемент(solid), который предназначен для построения конечно-элементой сетки в трехмерных тел произвольной формы. Обычно такие элементы имеют вид клина, призмы или параллелепипеда (рисунок 4.2.7, а). Так же, как и для пластин, можно задавать элементы повышенной точности с промежуточными узлами на их сторонах (рисунок 4.2.7, б).

 

а)
б)

Рисунок 4.2.7 – Объемные конечные элементы

 

Интересной разновидностью объемного элемента является осемметричный (axisymmetric) конечный элемент. Такие элементы изображаются как плоские треугольники, но в действительности они моделируют объемное кольцо соответствующей формы (рисунок 4.2.8). Осемметричные элементы предназначены для моделирования напряженно-деформированного состояния в телах вращения (при условии осесимметричных нагрузок и закреплений).

 

Рисунок 4.2.8 – Оссеметричный конечный элемент

 

11. Пример использовании нескольких типов конечных элементов в одной модели

Многообразие видов конечных элементов и возможность их одновременного использования в одной модели позволяет оптимальным образом моделировать изделие. Эти особенности универсальных пакетов позволяют сочетать необходимую точность расчета при минимально возможных требованиях к вычислительной мощности.

Например, при моделировании железнодорожной цистерны все ее части можно описывать только твердотельными конечными элементами. Но для обеспечения мало-мальски приемлемой точности размер конечного элемента должен быть в несколько раз меньше толщины стенки цистерны, т.е. порядка нескольких миллиметров. В результате модель многометровой цистерны будет состоять из миллионов конечных элементов. Решение такой модели может занять несколько дней даже на достаточно мощной машине. Что парадоксально, в этом случае высокая точность не гарантирована, поскольку модель стенки цистерны, аппроксимированная по толщине всего двумя-тремя конечными элементами, может дать достаточно заметную погрешность.

Можно моделировать цистерну только пластинчатыми элементами. В этом случае модель самой емкости цистерны будет достаточно точной даже при больших размерах конечных элементов. Но помимо стенок, цистерна включает в себя элементы крепления, узлы заливной горловины и другие массивные элементы, весьма заметно влияющие на жесткость конструкции в целом. Моделирование их пластинчатыми элементами не обеспечит адекватной картины напряженно-деформированного состояния, что практически гарантирует заметную погрешность итогового расчета.

Наилучшим решением будет использовать пластинчатые элементы для моделирования стенок цистерны, и твердотельные элементы для моделирования массивных частей или областей со сложным напряженным состоянием. В единое целое их можно объединить, используя жесткие (rigid) элементы. Такое решение позволят обеспечить одновременно и высокую точность и высокую скорость расчета.

 

12. Задание параметров сетки конечных элементов

Сетку конечных элементов, в принципе, можно построить и в «ручном» режиме, указывая координаты узлов. Но чаще всего создание сетки конечных элементов происходит в автоматическом режиме, как правило, на базе геометрии детали.

Параметры сетки конечных элементов существенно влияет на точность и время выполнения конечно-элементного расчета. Важнейшими из них являются размер и форма конечного элемента.

Идеальная форма плоского элемента – равносторонний треугольник или квадрат, объемного элемента – равносторонняя пирамида или куб и т.д. Чем меньше разница между длиной сторон конечного элемента, тем меньше погрешность расчета, обусловленная самой математикой метода конечных элементов. Элементы, слишком вытянутые в одном направлении, могут негативно влиять на устойчивость проведения расчета и, опосредовано, на его точность. В универсальных пакетах существуют как средства контроля формы при построении сетки конечных элементов, так и возможность редактирования формы отдельных элементов.

Как правило, чем мельче сетка (меньше размеры конечных элементов), тем выше точность расчета. Но, если модель разбита на слишком большее число конечных элементов, то резко возрастает время расчета, а в ряде случаев (на недостаточно мощных машинах) расчет вообще становится практически невозможным. Поэтому перед разбиением геометрической модели на конечные элементы задают средний размер элемента и указывают, где необходимо сгущение или наоборот, допустимо разрежение сетки конечных элементов.

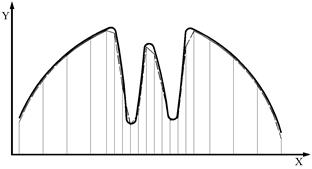
Остановимся подробней на причинах необходимости редактирования параметров сетки. При моделировании методом конечных элементов фактическая зависимость искомой функции Y от параметра X (например, значения напряжений в балке Y в зависимости от текущей координаты X) заменяется (аппроксимируется) набором отрезков. Значения расчетной функции на концах отрезков равны фактическому значению функции в этих точках. Принимается, что внутри элемента значение функции изменяется линейно.

Например, на рисунке 4.2.9 толстая линия – фактическое значение функции, а отрезки, выполненные штриховой линией – результат ее аппроксимации при выполнении расчета методом конечных элементов. Вертикальные тонкие линии показывают границы конечных элементов. Расстояние между отрезками и линией искомой функции характеризует погрешность расчета.

Если функция Y изменяется медленно и плавно (рисунок 4.2.9, а), то допустимо задавать относительно большие размеры конечных элементов. В результате даже при больших размерах конечных элементов погрешность будет невысока.

Но если функция Y имеет области, где она резко изменяется (как на рисунке 4.2.9, б-г), то результат МКЭ-расчета при аппроксимации крупными элементами может даже качественно не соответствовать реальности. Пример такой ошибки иллюстрирует рисунок 4.2.9, б. Результат расчета (штриховая линия) в центре диаграммы даже близко не соответствует фактическому значению искомой функции.

 

а)	б)
в)	г)

Рисунок 4.2.9 – Варианты разбиения на конечные элементы

 

Казалось бы, существует очевидно решение – уменьшить размеры конечных элементов, как показано на рисунке 4.2.9, в. Но в результате такой модернизации резко увеличится общее число конечных элементов и, соответственно, время расчета и потребные вычислительные ресурсы.

Оптимальным является вариант разбиения, показанный на рисунке 4.2.9, в. Там, где скорость изменения функции невелика, размеры конечных элементов оставляют большими. Размеры конечных элементов уменьшают только на тех участках, где функция резко изменяется. При таком подходе удается добиться того, что результаты расчета незначительно отличаются от фактических значений на всех участках изменения функции. Такую операцию еще называют сгущением сетки конечных элементов.

Сгущение сетки желательно выполнять в тех местах модели, где предполагаются резкое изменение напряжений (или, в общем случае, исследуемых параметров) по длине детали. Например, это могут быть элементы конструкции с резкими переходами в поперечных сечениях, связанными с наличием отверстий, канавок, надрезов и т.д. (т.н. концентраторы напряжений). Соответственно, менее густую сетку допустимо выполнять на участках, где напряжения меняются медленно. Кроме того, обычно сетку сгущают в окрестностях точек приложения нагрузок и закреплений, в зонах контакта тел, а также в зоне предполагаемого выпучивания при расчетах на устойчивость и собственные частоты.

Для управления густотой сеткой, которая строится на основе геометрии детали, в универсальных пакетах существуют специальные средства, что является одной из важных их особенностей, позволяющее, не теряя в точности, в десятки и сотни раз сократить время расчета сложной модели.

Безусловно, правильный выбор размеров конечных элементов требует определенного опыта, как в предметной области, так и в области конечно-элементных расчетов. Тем не менее, существуют стандартные приемы решения этой задачи. Например, часто первый расчет проводят на крупной сетке конечных элементов. Затем, на основании анализа картины распределения напряжений, намечают области, где необходимо сгустить сетку. Далее проводят несколько последовательных расчетов при постепенно уменьшающихся размерах элементов. Если после очередного уменьшения размеров элементов результаты расчета перестают заметно изменяться, то считается, что дальнейшее уменьшение размеров конечных элементов уже нецелесообразно с точки зрения повышения точности.

13. Задание нагрузок и закреплений

С математической точки зрения и нагрузки, и закрепления представляют собой граничные условия, наложенные на обобщенные перемещения узлов конечно-элементной модели исследуемого тела. При решении механической задачи единые граничные условия удобно разделять на закрепления (constraints) и нагрузки (loads). В универсальных пакетах для одной модели может быть несколько наборов произвольных (в том числе разнотипных) закреплений и нагрузок. При желании их можно комбинировать произвольным образом.

Закрепления представляют собой запрет на перемещение выбранного узла в том или ином направлении. Любой узел, в принципе, может перемещаться вдоль осей координат X, Y, Z или вращаться вокруг этих осей. Иными словами, он имеет шесть степеней свободы (degrees of freedom, DOF). Для решения механической задачи методом конечных элементов заключается в том, что исследуемое тело должно быть зафиксировано. Для этого достаточно указать на выбранные узлы конечно-элементной сетки и ограничить их степени свободы.

Иногда бывает удобно ограничить степени свободы узла, задав его координаты в цилиндрической (cylindrical) или сферической (spherical) системах координат. Например, так удобно задавать закрепление вала в радиальном подшипнике, когда необходимо запретить перемещение вдоль радиуса, но оставить возможным вращение вала и возможность его перемещение в осевом направлении.

Для механических задач нагрузка задается как сила (force) или пара сил (moment), перемещение (displacement) или угол поворота (enforced rotation) и, в некоторых специфических случаях, линейную (velocity) или угловую (rotational velocity) скорость и ускорение (acceleration, rotational acceleration). Нагрузки прикладываются к какому-то узлу (или узлам). Обычно для задания параметров нагрузки необходимо вызвать команду задание нагрузки (load) и выбрать необходимые узлы. Далее, в появившемся меню, следует выбрать значения составляющих нагрузки.

Распределенными нагрузками может быть, например, давление (pressure) или погонная сил (сила на единицу длины, force per length). Интересным видом распределенных нагрузок являются объемные нагрузки, вызванные весом тела или центробежной силой при вращении. Они прикладываемые ко всем конечным элементам, аппроксимирующим тело. После задания любого вида распределенных нагрузок машина автоматически рассчитывает силу, приходящуюся на один узел выбранного участка конечно-элементной сетки, с учетом размера и формы конечных элементов.

К тепловым нагрузкам относится температура (temperature), тепловыделение (мощность генерации тепла на единицу объема тела, heat generation), тепловой поток (тепловая энергия, переносимая через единицу площади, heat flux). В свою очередь, одним из источников теплового потока могут быть конвективный поток (convection) и радиационное излучение (radiation). Обязательным условием при проведении любого вида теплового расчета служит задание начальной температуры тела (начальное условие).

Например, при конвективным теплообмене жидкости или газы, находящиеся в контакте с твердым телом, либо отдают ему тепло (нагревают), либо получает от него тепло (охлаждают). Количество теплоты Q, Вт, проходящее через поверхность раздела площадью S, м², определяется зависимостью:

,

где a – коэффициент теплоотдачи, [a]=Вт/м²´^оС; Т _тело – температура твердого тела, ^оС; Т _О.С. – температура окружающей среды (жидкости или газа), ^оС.

Также как и для закреплений, при задании нагрузок возможно использование не только прямоугольной (rectangular), но также цилиндрической (cylindrical) или сферической (spherical) систем координат. Это может быть удобным, например, при задании контактных сил в сопряжении «вал – втулка».

В нагрузку могут быть преобразованы и результаты предыдущего расчета, не обязательно того же вида. Например, стандартным способом задания остаточных механических напряжений в теле служат результаты теплового расчета. Неравномерный нагрев тела вызывает его неравномерное тепловое расширение. Затем деформации, вызванные тепловым расширением, преобразуются в напряжения. Параметры тепловой нагрузки подобраны таким образом, чтобы термоупругие напряжения соответствовали заданным остаточным напряжениям.

 

14. Виды конечно-элементных расчетов. Статические расчеты

Рисунок 4.2.14 – Причина возникновения геометрической нелинейности

15. Виды конечно-элементных расчетов. Динамические расчеты

Динамические расчеты обеспечивают решение следующих типовых задач:

– анализ нестационарных переходных процессов в объекте при сравнительно кратковременном (импульсном) действии нагрузки (Transient Dynamic/Time History);

– исследование динамической реакции объекта на достаточно длительное периодическое воздействие внешних факторов (Frequency/Harmonic Response);

– определение собственных частот и форм колебаний (Normal Modes/Eigenvalues).

Под нестационарным переходным процессом обычно понимают поведение конструкции в начальный период времени, когда ее движение еще не установилось и складывается из собственных колебаний и вынужденного движения, вызванных приложенной нагрузкой. Результат анализ нестационарных процессов обычно представляется в виде графика переходного процесса, т.е. зависимости амплитуд колебаний элементов системы от времени. В результате расчета можно оценить время переходного процесса, максимальные и установившиеся значения исследуемых параметров, коэффициент демпфирования системы и т.д.

При исследовании поведения изделия при вынужденных колебаниях (или реакции на периодическое внешнее воздействие) результат обычно представляется в виде графиков зависимости амплитуды колебаний (деформаций) элементов конструкции в зависимости от частоты возмущающей нагрузки. Такую зависимость еще называют амплитудно-частотной характеристикой (АЧХ) изделия. Важным результатом такого исследования является определение диапазона опасных частот внешнего воздействия, при которых происходит наступление резонанса.

Например, на рисунке 4.2.16 приведены амплитудно-частотные характеристики механической системы, построенные для точек (точнее, узлов) 1 и 2. Из анализа графиков можно заключить, что при статическом нагружении (частота внешнего воздействия равна 0) деформация в точке 1 равна 7 мм, а в точке 2 – 0.9 мм. Зато при частоте внешней возмущающей силы, равной 60 Гц, возникает резонанс, и деформация в точке 1 возрастает до 29 мм, а в точке 2 – до 4.4 мм. Пропорционально возрастают и напряжения, что может привести к поломке системе при частоте возмущающей силы около частоты резонанса. Зато при высоких частотах возмущающей силы (более 300…400 Гц) из-за своей инерционности система не успевает за возмущающей силой и деформация в рассматриваемых точках стремится к нулю.

Собственными (свободными) колебаниями называются колебания, возникающие в системе вследствие внешнего толчка, вызывающего первоначальное отклонение, и продолжающиеся затем благодаря внутренним упругим силам, восстанавливающих равновесие. Период (частота) собственных колебаний зависит от формы и упругих свойств системы. В процессе колебаний пространственная система может принимать различные формы, которые называются собственными формами. Таких частот (мод), в принципе, бесконечное количество, но при колебаниях реальной конструкции обычно возникают только несколько первых (старших), причем наибольшая энергия колебаний сосредоточена на первой собственной частоте. Сравнение значений собственных частот и вероятных частот внешней возмущающей силы позволяет избежать возникновения резонансных колебаний в конструкции, заранее принять меры по снижению вибраций.

Рисунок 4.2.16 – Зависимость амплитуды колебаний различных частей конструкции в зависимости от частоты возмущающей нагрузки

Анализ форм собственных колебаний позволяет определить те места в конструкции, где деформации при колебаниях будут принимать наибольшие (или наименьшие) значения. Для сложных конструкций это далеко не тривиальная задача, решение которой позволяет существенно снизить наблюдаемый уровень вредных вибраций. Например, на некоторых режимах работы двигателя автомашины могут возникать достаточно мощные низкочастотные колебания, близкие к частоте собственных колебаний кабины машины. Если максимальные амплитуды этих колебаний будут локализоваться в районе педалей (т.е. там, где размещаются ступни водителя), то с точки зрения водителя вибрации будут недопустимо сильные. Но если чуть-чуть изменить конструкцию кабины (например, переместить на несколько миллиметров элементы жесткости), то в районе педалей окажется зона с минимальными амплитудами колебаний. В результате окажется (с точки зрения водителя), что вибрации исчезли.

В некоторых случаях может оказаться полезным наоборот, увеличивать амплитуду вибраций. Известно, что при точении колебания режущей кромки резца в диапазоне частот порядка 200…300 герц помогают образовываться мелкой (дробленной) стружке. Поэтому необходимо ввести резец в режим колебаний на заданной частоте. Для этого, в частности, необходимо, чтобы первая собственная частота резца была равна заданной. Но собственная частота цельного резца порядка нескольких килогерц. Один из самых простых способов снижения собственной частоты системы «резец – резцедержатель» – выполнить прорезь в теле резца. Подбирая расположение и глубину прорези, достаточно просто изменить собственную частоту колебаний части резца в районе режущей кромки с тем, чтобы она соответствовала заданному диапазону.

 

16. Представление результатов расчета

Результаты расчета можно просмотреть самыми разными путями. Например, самая полная информация о перемещениях, напряжениях и т.д. в каждом узле исследуемого тела записана в текстовом файле результатов. Это не всегда удобно, поскольку такой файл имеет большой размер. Поэтому обычно вначале визуально оценивают распределение расчетных параметров в теле, а затем уточняют значения параметров в элементах с экстремальными значениями.

Раскраска пластины отражает распределение расчетных параметров, в данном случае эквивалентных напряжений по фон Мизесу. Для грубой оценки значений расчетного параметра с правой стороны экрана размещается шкала (т.н. легенда), состоящая из цветных квадратиков. Возле каждого цветного квадратика шкалы стоит соответствующее ему среднее численное значение параметра. Как правило, холодным цветам (фиолетовый, синий, …) соответствует минимальное, а теплым (оранжевый, красный, …) – максимальное значение расчетного параметра.

В некоторых случаях бывает удобно представить результаты распределения расчетных параметров в виде графика зависимости параметра от, например, какой-нибудь координаты. При такой форме представления результатов легко уточнить места расположения экстремальных значений исследуемого параметра.

Следует отметить, что 16-тицветная раскраска в принципе не может позволить оценить точное значение параметра. Цветное изображение предназначено только для качественной оценки распределения исследуемого параметра (например, напряжений). При необходимости уточнить значение параметров, например, напряженно-деформированного состояния, в конкретном конечном элементе достаточно указать на него и получить полный список всех относящихся к нему расчетных параметров.

Следует хотя бы кратко упомянуть об оценке результатов, получаемых при прочностных расчетах. Для оценки напряжений по умолчанию обычно предлагается значения эквивалентных напряжения s_ЭКВ, вычисленные по энергетической гипотезе фон Мизеса (VonMises Stress):

где s_X, s_Y, s_Z – нормальные, а t_XY, t_YZ, t_XZ – касательные напряжения. Такой критерий, вытекающий из четвертой теории прочности, наиболее подходит для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию. С другой стороны, для хрупких материалов, для материалов, имеющих разное сопротивление на растяжение и сжатие, для ламинированных материалов, композитов и т.д. может оказаться целесообразным оценивать предельно допустимые напряжения по другим критериям. Например, это могут быть значения наибольших главных напряжений (MajorPrn Stress), допустимые деформации (Translation), максимальные сдвиговые напряжения в верхних волокнах пластины (MaxShear Stress) и т.д. Выбор нужного критерия является важнейшим этапом в оценке результатов расчета и, к сожалению, определяется только знанием и опытом проектировщика.

Рисунок 3 – Примеры представления результатов гидродинамических расчетов

 

Оценка уровня шума, который будет производить изделие во время эксплуатации особенно важна для автомобилестроения и в гражданской авиации. Например, шум авиадвигателей явля­ется одним из основных критери­ев качества гражданского самолета, поскольку самолеты с высоким уровнем шума аэропорты ряда стран просто не прини­мают.

К задачам акустического анализа относится определение параметров акустического поля (интенсивность, спектральный состав звука) в выбранном объеме. В качестве исходных данных необходима геометрия исследуемого пространства, спектральная характеристика и мощность источника звука. В качестве примеров модулей MSC.Software, помогающих решать акустические задачи, можно назвать Actran, Akusmod.

Общая структура универсального пакета

Логически универсальный пакет состоит из трех основных частей: препроцессора, расчетного ядра и постпроцессора. Препроцессор обеспечивает формирование исходных данных для расчета. Его задачи:

– создание или импорт геометрии изделия;

– задание свойств материала (или материалов);

– создание сетки конечных элементов;

– задание нагрузок и условий закрепления;

– формирование матрицы исходных данных и передачу их на расчет.

Расчетное ядро (решатель, solver) – самая главная часть пакета, производящая собственно сам расчет методом конечных элементов. Как правило, решатель включает несколько отдельных модулей, ориентированных на тот или иной вид расчета (механический, тепловой и т.д.).

Постпроцессор представляет результаты расчета в удобной для пользователя форме. Например, распределение механических напряжений или температур в модели часто показывают изменением цвета (раскрашиванием). При этом минимальное значение величины обычно соответствует фиолетовому цвету, а максимальное – красному. Аналогично, деформация модели на экране утрированна, но пропорциональна расчетной деформации и т.д.

Типовая схема взаимодействия препроцессора, решателя, постпроцессора и CAD-программ представлена на рисунке 4. Геометрическая модель изделия, созданная в CAD-модуле, передается в препроцессор. Проектировщик в препроцессоре создает сетку конечных элементов, используя импортированную геометрическую модель изделия. Далее прикладываются нагрузки, закрепления и препроцессор передает сформированную матрицу исходных данных решателю для расчета. Решатель производит расчет и передает результаты в виде таблицы в постпроцессор. Постпроцессор визуализирует результаты расчета в удобном для конструктора виде. Проектировщик по результатам расчета изменяет конструкцию (геометрию) проектируемого изделия в CAD-программе и измененную геометрию опять передает в препроцессор. Далее цикл повторяется до нахождения приемлемого решения.

Пре/постпроцессор обычно представляет собой отдельную программу. Например, для ANSYS это PrePost, Workbench, для NASTRAN – PATRAN, Femap.

 

Рисунок 4 – Схема взаимодействия препроцессора, решателя, постпроцессора и CAD-программы

7. Основные этапы решения задачи с использование МКЭ

При расчете в конечно-элементном пакете выполняется ряд практически обязательных последовательных шагов. Перечислим их.

1. Создать или импортировать из другого пакета геометрию тела. Существуют два основных пути получения геометрии исследуемо­го тела. Возможно сделать это либо графическими средствами CAE-пакета, либо им­портируя геометрию из CAD-пакетов. Первый вариант чаще используется расчетчиками старой школы, но второй вари­ант практичней, поскольку сокращается время на подготовку геометрии и, в ряде случаев, позволяет создать ассоциативность между геометрической и расчетной моделью. Кроме того, графические возможности CAE-пакетов, как правило, сильно проигрывают по сравнению с возможностями CAD-пакетов. Все-таки CAE-пакеты ориентированы на расчет, а не на создание геометрии.

2. Проконтролировать полученную геометрию. При импорте или редактировании геометрии не исключено появление ошибок. Наиболее часто появляются тончайшие щели между поверхностями или своеобразные «осколки» поверхностей микроскопического размера. И тот, и другой вид дефектов на экране практически невидимы. Но при попытке разбить такие дефектные тела сеткой конечных элементов появляется сообщение об ошибке (это в лучшем случае). В худшем случае расчет проходит «успешно», но результаты получаются весьма нетривиальные… Поэтому в CAE-пакетах присутствуют достаточно развитые средства контроля и «лечения» наиболее характерных дефектов геометрии.

Типовые приемы улучшения взаимодействия CAD-CAE пакетов:

a) Подбор промежуточного формата для импорта (Parasolid – *.x_t, ACIS – *.sat и т.д.)

b) Строить тела только с применение операций типа «выдавливание», «вращение», «бобышка», «вырез».

c) Удаление скруглений, непринципиальных с точки зрения прочности.

d) Удаление мелких (в сравнении с габаритными размерами детали) элементов геометрии (фасками, канавками для выхода резьбы, отверстиями малого диаметра и т.д.).

3. Задать механические и термические свойства материала тела.

4. Задать тип конечных элементов.

5. Разбить тело на конечные элементы. При разбиении границы конечные элементы выглядят как ячейки сетки («mech»), охватывающей тело. Точки, в которых КЭ соединяют­ся между собой, называются узлы («node») сетки. Поэтому эту про­цедуру часто называют созданием сетки конечных элементов. Как правило, получение сетки конечных элементов происходит в автоматическом режиме. При этом можно задать параметры формы конечных элементов, сгустить или разредить сетку в требуемой области, вручную исправить неудачные участки сетки и т.д.

6. Проконтролировать полученную сетку конечных элементов. Этот этап необходим, в первую очередь, после «ручного» редактирования сетки конечных элементов. Например, при копировании может получиться набор конечных элементов, узлы которых имеют общие координаты. Но, тем не менее, они оказываются не соединены между собой. Для объединения в единую сетку надо, чтобы каждый узел принадлежал как минимум двум элементам. Поэтому приходится удалять лишние узлы и связывать оставшиеся узлы с несколькими элементами. Для контроля и «лечения» сетки конечных элементов в CAE-пакетах присутствуют достаточно развитые средства.

7. Задать нагрузки, действующие на тело.

8. Задать начальные и граничные условия.

Начальные условия это, например, начальное распределение температур или остаточных напряжений в теле. Граничные условия – где и каким образом тело зафиксировано от смещения или поворота.

9. Произвести расчет.

На одной и той же конечно-элементной модели можно проводить расчет, напри­мер, и на прочность, и на устойчивость конструкции, и на распределение температур. Поэтому необходимо задать тип расчета.

10. Просмотреть результаты расчета.

Наиболее часто результаты расчета просматривают в виде де­формированной и раскрашенной модели. Обычно деформация модели представляет деформацию тела (с большим увеличением), а напряже­ния – в виде распределения цветов модели – от красного до синего. При этом большим напряжениям соответствует красный цвет, меньшим – желтый и т.д. Кроме того, для подробного изучения распределения изучаемого параметра в модели (например, температуры при тепловом или главных напряжений при механическом расчетах) возможно вывести значения соответствующих параметров в текстовый файл.