3.1. Характеристика ряда динамики.
3.2. Оценка уравнения Тренда.
3.3. Основная тенденция изменения показателей во времени.
3.4. Прогнозный интервал показателя.
IV. Эконометрический анализ данных на основе регрессионной модели:
4.1. Анализ исходных данных
Построим графики зависимостей x(t), y(t), y(x) (рис. 2 – 4):
Рис. 2 Рис. 3 Рис. 4
Выводы: Графический анализ исходных данных показывает, что для построения модели регрессии может быть использовано уравнение ____:
y(x) = ____________________.
4.2. Построение модели регрессии y(x).
В соответствии с методом наименьших квадратов (МНК) для определения параметров ɑ0 и ɑ1 решим систему уравнений:
 .
.
Для удобства вычислений параметров системы уравнений составим таблицу
Таблица 4
 Исходя из Таблицы 4, система уравнений с численными значениями параметров имеет вид:
Исходя из Таблицы 4, система уравнений с численными значениями параметров имеет вид:
Решим систему уравнений по правилу Крамера:
 _____________,
_____________,
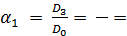 _____________.
_____________.
Вывод: Модель регрессии с численными коэффициентами имеет вид:
 _______________
_______________
4.3. Анализ качества модели регрессии – анализ остатков
Определим остатки по формуле (см. Таблица 5):

Таблица 5
| t
| xi
| yi
| 
| 
| ui – ui-1
| (ui – ui-1)2
| ui2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ∑
|
|
|
|
|
|
|
|
Вычислим коэффициент Дарбина-Уотсона d r (промежуточные вычисления выполнены в Таблице 5):
 ____________ ≈ _______.
____________ ≈ _______.
Коэффициент dr является критерием проверки гипотезы о наличии автокорреляции в остатках генеральной совокупности. По таблице Дарбина-Уотсона находим для заданного уровня значимости ɑ = 0,05 и числа наблюдений n = теоритические значения dL = __________________________ и du = _______.
Для сравнения табличных и расчетных значений построим схему:
| Присутствует автокорр.
«+»
| Зона неопределен-ности
| Автокорр. отсутствует
| Зона неопределен-ности
| Присутствует автокорр.
«-»
|
|
| dL
| | du
| | 4-du
| | 4-dL
|
|
|
|
|
|
|
|
|
|
|
|
| | | | | | | | | | | | | |
Рис. 5
Вывод: Критерий Дарбина-Уотсона dr = __? подтверждает гипотезу о автокорреляции в остатках, поскольку:
4.4. Корреляционный анализ данных.
Рассчитаем линейный коэффициент корреляции по формуле:
 .
.
Выполним промежуточные вычисления (Таблица 6).
Таблица 6
| n
| x
| y
| x∙y
| x2
| y2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ∑
|
|
|
|
|
|
| Среднее значение
|
|
|
|
|
|
Величина линейного коэффициента корреляции равна:
 _______________________________.
_______________________________.
Вывод: Величина коэффициента корреляции rxy = ____ свидетельствует
о _________________ __________________ связи между показателями x и y.
(направление связи) (сила связи)
Выполним проверку статистической значимости линейного коэффициента корреляции с помощью критерия Стьюдента (t – статистики):
 __________.
__________.
Табличное значение критерия Стьюдента определим, используя группу функций «Статистические», функция СТЬЮДРАСПОБР (для MS Excel – 207; в зависимости от года MS Excel название функции может немного меняться).
t табл. (ɑ = 0,005; n-k-1 = ___) = _________.
где ɑ = 0,05 – уровень значимости, n – число заданных значений y;
k – количество независимых переменных (х) в уравнении регрессии.
Сравним t расч. и t табл.: t расч. ___ t табл.
Вывод: Проверка статистической значимости линейного коэффициента корреляции rxy показывает, что коэффициент значимо отличается от нуля.
Общий вывод: Корреляционный анализ показал, что между показателями x и y имеется __________________ взаимосвязь.
4.5. Статистический анализ параметров уравнения регрессии.
Проверку статистической значимости парметров уравнения регрессии выполним с помощью критерия Стьюдента (t – статистики).
Рассчитаем значения t – статистики t расч. и сравним с tтабл.
 ______________.
______________.
 .
.
t табл. (ɑ, n -2) = t табл. (0,05; ___) =.
 ___ t табл.
___ t табл.
Вывод: Параметр уравнения регрессии ɑ0 статистически ___ значим, поэтому его следует __ в модели. Параметр уравнения регрессии ɑ1 статистически ___ значим, следовательно, фактор x оказывает статистически ___ значимое воздействие на изменение y. Его следует _____________ в модели.
4.6. Оценка качества модели в целом по коэффициенту детерминации.
1) Определим коэффициент детерминации:  .
.
Для упрощения расчетов составим Таблицу 7.
Таблица 7
Среднее значение показателя:  ________
________
 ________________ ≈.
________________ ≈.
Вывод: На ___% вариация признаков y (________________________) объясняется влияние фактора х (_____________________________________________).
2) Оценим статистическую значимость R 2.
Проверяем нулевую гипотезу о том, что коэффициент детерминации в генеральной совокупности равен нулю. Проверку гипотезы осуществляем с помощью F – критерия (критерия Фишера). Для k = 1 – число факторов в модели:
 ________________ ≈ _________.
________________ ≈ _________.
F табл. (ɑ, n-k-1, k) = t табл. (0,05; ___; ___) = ____.
 _____ F табл. (ɑ, n-k-1, k).
_____ F табл. (ɑ, n-k-1, k).
Вывод: Проверка статистической значимости коэффициента детерминации R2 показывает, что R2 ___ значимо отличается от нуля. Нулевая гипотеза ___ отклоняется с заданным уровнем доверительной вероятности ɑ = 0,05.
Общий вывод: Построенная для прогноза регрессионная модель ____ адекватна.



 .
. Исходя из Таблицы 4, система уравнений с численными значениями параметров имеет вид:
Исходя из Таблицы 4, система уравнений с численными значениями параметров имеет вид: _____________,
_____________,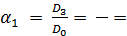 _____________.
_____________. _______________
_______________


 ____________ ≈ _______.
____________ ≈ _______. .
. _______________________________.
_______________________________. __________.
__________. ______________.
______________. .
. ___ t табл.
___ t табл. .
.



 ________
________ ________________ ≈.
________________ ≈. ________________ ≈ _________.
________________ ≈ _________. _____ F табл. (ɑ, n-k-1, k).
_____ F табл. (ɑ, n-k-1, k).


