Первообразная и неопределенный интеграл.
Функция 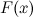 называется первообразной для функции
называется первообразной для функции  на промежутке
на промежутке 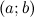 , конечном или бесконечном, если функция
, конечном или бесконечном, если функция 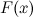 дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:

Функция F(x) называется первообразной для функции f(x), если справедливо равенство F’(x)=f(x).
В общем случает, если для функции f(x) есть первообразная F(x), для которой выполняется равенство, то f(x) +с так же первообразная для функции f(x), где с – произвольная константа.
Функция вида F(x)+c – семейство первообразных.
(О бесконечном множестве первообразных для функции)
Если функция 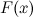 является первообразной для функции
является первообразной для функции  на некотором промежутке, то и функция
на некотором промежутке, то и функция  , где
, где 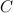 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции  на рассматриваемом промежутке.
на рассматриваемом промежутке.
(Об общем виде первообразной для функции)
Если функции 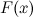 и
и  - две любые первообразные функции
- две любые первообразные функции  , то их разность равна некоторой постоянной, то есть
, то их разность равна некоторой постоянной, то есть

Теорема 1. Пусть F(x) некоторая первообразная для f(x), тогда все первообразные представлены в виде семейства f(x)+с, где с – константа.
Док-во. Пусть F(x) –первообразная для f(x).
Фи(х)= f(x)
По условию теоремы F(x) так же первообразная f(x)= F(x)
Вычтем: фи(х)- f(x)=0
По св-ву производной:
(фи(х)- f(x))’=0
Следовательно:
фи(х)- f(x)=с
фи(х)- f(x)+с
Следствие: любые две первообразные для одной и той же функции отличаются разве лишь на постоянное число.
Семейство первообразных f(x)+c функции f(x) называют неопределенными интегралами и обозначают значком интеграла.
Теорема 2 (без док-ва).
Если f(x) подинтегральная функция непрерывная на некотором промежутке, то для нее существет первообразная и неопределенный интеграл.
Совокупность всех первообразных функции  , определенных на заданном промежутке, называется неопределенным интегралом от функции
, определенных на заданном промежутке, называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом 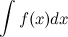 . То есть
. То есть

Знак  называется интегралом,
называется интегралом,  - подынтегральным выражением,
- подынтегральным выражением,  - подынтегральной функцией, а
- подынтегральной функцией, а  - переменной интегрирования.
- переменной интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции  называется интегрированием функции
называется интегрированием функции  . Интегрирование представляет собой операцию, обратную дифференцированию.
. Интегрирование представляет собой операцию, обратную дифференцированию.
Т. о. с геометрической точки зрения неопределенный интеграл есть семейство интегралов кривых, полученных х в результате сдвига интегральной кривой у= f(x) в направлении оси ОУ вверх/вниз на отрезок произвольной длины с.
Теорема о среднем.
Если f (x) непрерывна на отрезке [ a, b ], то существует точка  , такая что
, такая что  .
.
 Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения.
Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения.  Тогда
Тогда 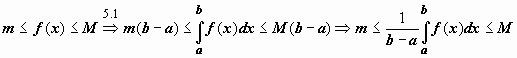 . Число
. Число  заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка
заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка  , такая что
, такая что 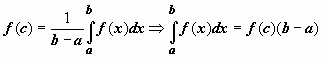 .
.
 Это свойство имеет простую геометрическую интерпретацию: если
Это свойство имеет простую геометрическую интерпретацию: если 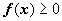 непрерывна на отрезке [ a, b ], то существует точка
непрерывна на отрезке [ a, b ], то существует точка  такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [ a, b ] и высотой f (c) (на рисунке выделен цветом).
такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [ a, b ] и высотой f (c) (на рисунке выделен цветом).
Важное следствие
| Утверждение:
|
Пусть 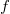 — непрерывна на — непрерывна на 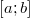 . Тогда на этом отрезке у неё существует неопределённый интеграл. . Тогда на этом отрезке у неё существует неопределённый интеграл.
|
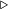
|
 В силу непрерывности функции на отрезке и теоремы Барроу
В силу непрерывности функции на отрезке и теоремы Барроу  — одна из первообразных.
Значит, неопределённый интеграл существует. — одна из первообразных.
Значит, неопределённый интеграл существует.
|
Формула Ньютона-Лейбница
| Теорема (формула Ньютона-Лейбница):
|
Пусть 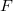 дифференцируема на дифференцируема на 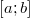 , её производная , её производная 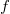 интегрируема на этом же отрезке. Тогда интегрируема на этом же отрезке. Тогда 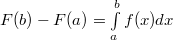
|
| Доказательство:
|
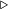
|
Так как 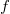 — интегрируема, то — интегрируема, то  равен пределу интегральных сумм при любой системе промежуточных точек для равен пределу интегральных сумм при любой системе промежуточных точек для  .
Поэтому, если .
Поэтому, если  — разбиение — разбиение 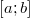 , то , то
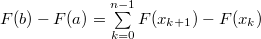 . Так как . Так как 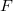 дифференцируема, то, применив для каждого промежутка из разбиения формулу Лагранжа, получим: дифференцируема, то, применив для каждого промежутка из разбиения формулу Лагранжа, получим:


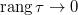 , следовательно, правая часть стремится к интегралу, левая — постоянна. Значит, в пределе, получаем нужную формулу. , следовательно, правая часть стремится к интегралу, левая — постоянна. Значит, в пределе, получаем нужную формулу.
|

|
Следствие
Объединяя эту теорему со следствием к теореме Барроу получаем следующий факт:
| Утверждение:
|
Пусть 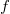 — непрерывна на — непрерывна на 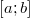 , , 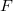 — одна из первообразных. Тогда — одна из первообразных. Тогда 
|
Формулы
]Вычисление определенного интеграла по частям
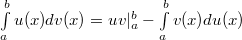
Формула Ньютона-Лейбница.
Если f (x) непрерывна на отрезке [ a, b ], и F (x) - некоторая первообразная функции  , то
, то 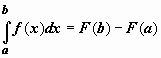 .
.
 Док-во. Мы установили, что функция
Док-во. Мы установили, что функция 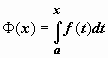 - первообразная непрерывной f (x). Так как F (x) - тоже первообразная, то Ф(x) = F (x) + C. Положим в этом равенстве x = a. Так как
- первообразная непрерывной f (x). Так как F (x) - тоже первообразная, то Ф(x) = F (x) + C. Положим в этом равенстве x = a. Так как  , то
, то  . В равенстве
. В равенстве 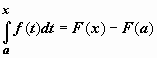 переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x, верхний предел x обозначим b. Окончательно,
переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x, верхний предел x обозначим b. Окончательно, 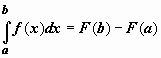 .
.
 Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом:
Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом:  (здесь
(здесь  читается как "подстановка от a до b "), поэтому формулу Ньютона-Лейбница обычно записывают так:
читается как "подстановка от a до b "), поэтому формулу Ньютона-Лейбница обычно записывают так:  .
.
 Пример применения формулы Ньютона-Лейбница:
Пример применения формулы Ньютона-Лейбница:  .
.
Первообразная и неопределенный интеграл.
Функция 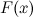 называется первообразной для функции
называется первообразной для функции  на промежутке
на промежутке 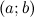 , конечном или бесконечном, если функция
, конечном или бесконечном, если функция 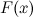 дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:

Функция F(x) называется первообразной для функции f(x), если справедливо равенство F’(x)=f(x).
В общем случает, если для функции f(x) есть первообразная F(x), для которой выполняется равенство, то f(x) +с так же первообразная для функции f(x), где с – произвольная константа.
Функция вида F(x)+c – семейство первообразных.
(О бесконечном множестве первообразных для функции)
Если функция 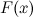 является первообразной для функции
является первообразной для функции  на некотором промежутке, то и функция
на некотором промежутке, то и функция  , где
, где 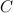 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции  на рассматриваемом промежутке.
на рассматриваемом промежутке.
(Об общем виде первообразной для функции)
Если функции 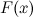 и
и  - две любые первообразные функции
- две любые первообразные функции  , то их разность равна некоторой постоянной, то есть
, то их разность равна некоторой постоянной, то есть

Теорема 1. Пусть F(x) некоторая первообразная для f(x), тогда все первообразные представлены в виде семейства f(x)+с, где с – константа.
Док-во. Пусть F(x) –первообразная для f(x).
Фи(х)= f(x)
По условию теоремы F(x) так же первообразная f(x)= F(x)
Вычтем: фи(х)- f(x)=0
По св-ву производной:
(фи(х)- f(x))’=0
Следовательно:
фи(х)- f(x)=с
фи(х)- f(x)+с
Следствие: любые две первообразные для одной и той же функции отличаются разве лишь на постоянное число.
Семейство первообразных f(x)+c функции f(x) называют неопределенными интегралами и обозначают значком интеграла.
Теорема 2 (без док-ва).
Если f(x) подинтегральная функция непрерывная на некотором промежутке, то для нее существет первообразная и неопределенный интеграл.
Совокупность всех первообразных функции  , определенных на заданном промежутке, называется неопределенным интегралом от функции
, определенных на заданном промежутке, называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом 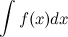 . То есть
. То есть

Знак  называется интегралом,
называется интегралом,  - подынтегральным выражением,
- подынтегральным выражением,  - подынтегральной функцией, а
- подынтегральной функцией, а  - переменной интегрирования.
- переменной интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции  называется интегрированием функции
называется интегрированием функции  . Интегрирование представляет собой операцию, обратную дифференцированию.
. Интегрирование представляет собой операцию, обратную дифференцированию.
Т. о. с геометрической точки зрения неопределенный интеграл есть семейство интегралов кривых, полученных х в результате сдвига интегральной кривой у= f(x) в направлении оси ОУ вверх/вниз на отрезок произвольной длины с.



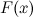 называется первообразной для функции
называется первообразной для функции  на промежутке
на промежутке 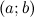 , конечном или бесконечном, если функция
, конечном или бесконечном, если функция 
 , где
, где 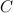 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции  на рассматриваемом промежутке.
на рассматриваемом промежутке. - две любые первообразные функции
- две любые первообразные функции 
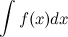 . То есть
. То есть
 называется интегралом,
называется интегралом,  - подынтегральным выражением,
- подынтегральным выражением,  - переменной интегрирования.
- переменной интегрирования. , такая что
, такая что  .
.  Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения.
Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения.  Тогда
Тогда 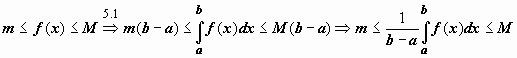 . Число
. Число  заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка
заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка 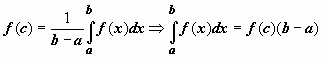 .
. 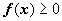 непрерывна на отрезке [ a, b ], то существует точка
непрерывна на отрезке [ a, b ], то существует точка 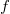 — непрерывна на
— непрерывна на 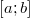 . Тогда на этом отрезке у неё существует неопределённый интеграл.
. Тогда на этом отрезке у неё существует неопределённый интеграл.
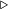
 В силу непрерывности функции на отрезке и теоремы Барроу
В силу непрерывности функции на отрезке и теоремы Барроу  — одна из первообразных.
Значит, неопределённый интеграл существует.
— одна из первообразных.
Значит, неопределённый интеграл существует.
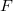 дифференцируема на
дифференцируема на 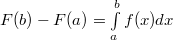
 равен пределу интегральных сумм при любой системе промежуточных точек для
равен пределу интегральных сумм при любой системе промежуточных точек для  .
Поэтому, если
.
Поэтому, если 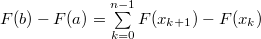 . Так как
. Так как 

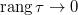 , следовательно, правая часть стремится к интегралу, левая — постоянна. Значит, в пределе, получаем нужную формулу.
, следовательно, правая часть стремится к интегралу, левая — постоянна. Значит, в пределе, получаем нужную формулу.


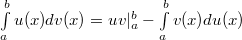
 , то
, то 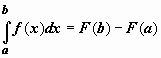 .
. 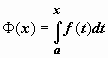 - первообразная непрерывной f (x). Так как F (x) - тоже первообразная, то Ф(x) = F (x) + C. Положим в этом равенстве x = a. Так как
- первообразная непрерывной f (x). Так как F (x) - тоже первообразная, то Ф(x) = F (x) + C. Положим в этом равенстве x = a. Так как  , то
, то  . В равенстве
. В равенстве 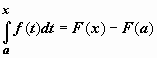 переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x, верхний предел x обозначим b. Окончательно,
переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x, верхний предел x обозначим b. Окончательно,  (здесь
(здесь  читается как "подстановка от a до b "), поэтому формулу Ньютона-Лейбница обычно записывают так:
читается как "подстановка от a до b "), поэтому формулу Ньютона-Лейбница обычно записывают так:  .
.  .
.

