

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Обозначим ℝ+ через интервал [0,∞). Пусть v (x) это любая функция v: (0, ∞)
→ (0, ∞) такая, что ∃ c, d 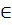 ℝ+ такие, что:
ℝ+ такие, что:
(1) ∀ х, v(x) < c, и
(2) ∀ х < d, v(x) = 0
Далее функция f: [0,∞) → [0,∞) заданная ниже, при действительном значении большем единицы именуемая «фрактальным преобразованием» v ().
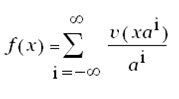
Эта запись ~ следующей:

Чтобы показать, что f (x) определена должным образом, нам нужно показать
что f (x) существует ∀ х > 0.
Пусть х 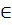 ℝ+. По условию (1) ∀ i справедливо, что v (x
ℝ+. По условию (1) ∀ i справедливо, что v (x 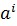 ) < c из чего следует
) < c из чего следует

т.е. левая сумма v (x 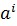 ) /
) / 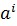 от i = 0 до ∞ существует. Т.к. а > 1, ∃ n
от i = 0 до ∞ существует. Т.к. а > 1, ∃ n 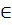 ℤ
ℤ 
x / 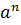 n < d ⇒∀ i > n имеем x /
n < d ⇒∀ i > n имеем x / 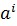 < d ⇒ по условию (2) ∀ i > n имеем v (x /
< d ⇒ по условию (2) ∀ i > n имеем v (x / 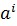 ) = 0.
) = 0.
Таким обр.,
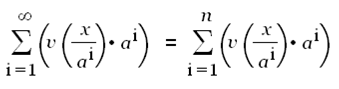
что однозначно существует. Поскольку

⇒ ∃ f (x).
В качестве первой теоремы математики временнóй волны ноль имеем:
Теорема 1: ∀ х  0, f (ax) = af (x).
0, f (ax) = af (x).
доказательство
пусть х 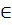
 , тогда
, тогда
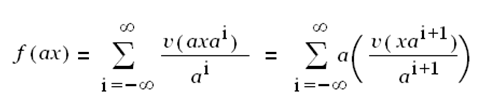
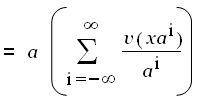
= af (x) QED
2. Математическая дефиниция временнóй волны
Функция, представляющая временнýю волну, есть фрактальная трансформанта пилообразной функции. Дадим определение последней. Для этого рассмотрим множество 384 чисел 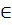 ℤ≥0, известных как расчётные точки временной волны:
ℤ≥0, известных как расчётные точки временной волны:
0 0 0 2 7 4 3 2 6 8
13 5 26 25 24 15 13 16 14 19
17 24 20 25 63 60 56 55 47 53
36 38 39 43 39 35 22 24 22 21
29 30 27 26 26 21 23 19 57 62
61 55 57 57 35 50 40 29 28 26
50 51 52 61 60 60 42 42 43 43
42 41 45 41 46 23 35 34 21 21
19 51 40 49 29 29 31 40 36 33
29 26 30 16 18 14 66 64 64 56
53 57 49 51 47 44 46 47 56 51
53 25 37 30 31 28 30 36 35 22
28 32 27 32 34 35 52 49 48 51
51 53 40 43 42 26 30 28 55 41
53 52 51 47 61 64 65 39 41 41
22 21 23 43 41 38 24 22 24 14
17 19 52 50 47 42 40 42 26 27
27 34 38 33 44 44 42 41 40 37
33 31 26 44 34 38 46 44 44 36
37 34 36 36 36 38 43 38 27 26
30 32 37 29 50 49 48 29 37 36
10 19 17 24 20 25 53 52 50 53
57 55 34 44 45 13 9 5 34 26
32 31 41 42 31 32 30 21 19 23
43 36 31 47 45 43 47 62 52 41
36 38 46 47 40 43 42 42 36 38
43 53 52 53 47 49 48 47 41 44
15 11 19 51 40 49 23 23 25 34
30 27 7 4 4 32 22 32 68 70
|
|
66 68 79 71 43 45 41 38 40 41
24 25 23 35 33 38 43 50 48 18
17 26 34 38 33 38 40 41 34 31
30 33 33 35 28 23 22 26 30 26
75 77 71 62 63 63 37 40 41 49
47 51 32 37 33 49 47 44 32 38
28 38 39 37 22 20 17 44 50 40
32 33 33 40 44 39 32 32 40 39
34 41 33 33 32 32 38 36 22 20
20 12 13 10
Эти значения получены путём особых преобразований над множеством 64
чисел. Под множеством 64 чисел подразумевается количество линий,
отличающее соседние гексаграммы в последовательности правителя Вэня.
Об этом шла речь в книге. Полученный таким образом ряд чисел даёт
исходные значения для математической дефиниции временнóй волны.
Определим w(i) как i-тое значение этого множества, используя индексацию с
отсчётом от нуля. Имеем:
i 0 1 2 3 4 5 …
w(i) 0 0 0 2 7 4 …
распространим w до функции w I(): ∀ i 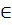
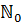 , w I(i) = w I(i mod 384), где i mod 384 есть остаток деления i на 384. Так, к примеру, w I(777) = w(777 mod 384) = w(9) = 8.
, w I(i) = w I(i mod 384), где i mod 384 есть остаток деления i на 384. Так, к примеру, w I(777) = w(777 mod 384) = w(9) = 8.
Запись w(9) = 8означает, что десятая расчётная точка, которой присвоен № 9 (в связи с тем, что первой присвоен № 0) имеет значение 8 (см. последнее число первого ряда в таблице трёхсот восьмидесяти четырёх чисел выше).
w I() есть дискретная функция, определённая только для x 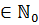 . Теперь ∀ x
. Теперь ∀ x 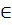 ℝ+ пусть v(x) будет значением, полученным линейной интерполяцией между значениями w I(⌊ x ⌋) и w I(⌈ x ⌉), где ⌊ x ⌋ и ⌈ x ⌉ соответственно пол и потолок от x. Формально v(x) определена как:
ℝ+ пусть v(x) будет значением, полученным линейной интерполяцией между значениями w I(⌊ x ⌋) и w I(⌈ x ⌉), где ⌊ x ⌋ и ⌈ x ⌉ соответственно пол и потолок от x. Формально v(x) определена как:
w I(⌊ x ⌋) + (x – ⌊ x ⌋) · [(w I(x + 1) – w I(x)]
или в расширенной форме:
v(x) = w(⌊ x ⌋ mod 384) + (x – ⌊ x ⌋) · [w(⌈ x ⌉ mod 384) – w(⌊ x ⌋ mod 384)].
Теперь рассмотрим фрактальную трансформанту f (x) от v(x), полагая а = 64:
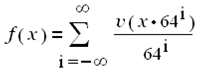
или, что то же:
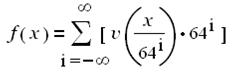
Функция f (x) существует, ибо
(1) ∀ x, v(x) < 80, и
(2) ∀ x < 3, v(x) = 0.
Фрактальная функция t (x), представляющая временнýю волну и вырисовываемая компьютерной программой является простым преобразованием f (x) делением на  :
:

где х = время в днях до шести утра по нью-йоркскому времени в дату зеро. Временнáя волна обращается в нуль только в одной точке: когда х = 0. При положительном x значение волны так же положительно. В качестве нулевой точки для функции временной волны выбран момент времени, отвечающий нулевой абсциссе. Обычно речь идёт о 6:00 восточного времени 21 декабря 2012 года: этот день известен как дата зеро. Таким обр., временная волна положительна для всех точек во времени, предшествующих дате зеро. Временная волна обнуляется лишь в начале координат и не определена в области до нуля. Увеличение на  используется для удобства оси Y графика. Итак, значение t (), в 6 утра в дату зеро:
используется для удобства оси Y графика. Итак, значение t (), в 6 утра в дату зеро:
|
|
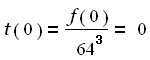
Значение t () в 6 утра восточного поясного времени накануне дня зеро:

где f (1) = (365 – 1)/384 = 91/96 = (7·13)/(6·16) т.е. f (1) 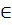 ℚ
ℚ
Значение t () для полдня восточного поясного времени на десятый день назад
от дня зеро (11 декабря):
t (9,75) =  · f (9,75) =
· f (9,75) =  · 795/64 =
· 795/64 =  ·3·5·53
·3·5·53
Значение t () для 6 утра нью-йоркского времени для момента, отстоящего от точки зеро на 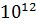 дней (т.е. 2 миллиарда 737 миллионов 888 тысяч 267 лет назад) составляет
дней (т.е. 2 миллиарда 737 миллионов 888 тысяч 267 лет назад) составляет
t (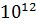 ) = 5.192.046,655.436.198
) = 5.192.046,655.436.198  134993213/26
134993213/26
Эти значения не зависят от выбора нулевой даты. Значения временной волны в любое заданное время не есть функция от времени самого по себе, но представляет собой пересчёт разницы между заданным моментом времени и нулевой точкой волны.
«Направление» графика противоположно обычно принятому в декартовых координатах. График типичной алгебраической функции f (x) начинается с левого края и идёт направо вдоль оси абсцисс с ростом х. В случае временнóй волны ситуация зеркальна: график идёт справа налево с увеличением аргумента: то есть, с увеличением дней до точки зеро.
Эмпирические соответствия функции f (x) для первых 24 целых х [ прим. пер. ]:
ℚ
1) (7·13)/(3· 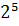 )
)
2)  /(7·3)
/(7·3)
3) 41/ 
4) 23/3
5) 3011/(7·6·16) = 3011/(7·3· 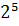 )
)
6) 3
7) 283/(3· 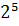 )
)
8) (71·2)/(7·3)
9) 137/ 
10) 41/3
11) (29·127)/(7·3· 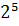 )
)
12) 26
13) (47·53)/(3· 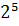 )
)
14) (13·8·5)/(7·3)
15) (83·3)/ 
16) = 10)
17) (443·  )/(7·3·
)/(7·3· 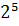 )
)
18) 14
19) (5·383)/(3· 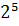 )
)
20) 373/(7·3)
21) (3·131)/ 
22) (2·31)/3
23) 17123/(7·3· 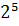 )
)
24) 63
Видно, что f (x) принимает целые значения, когда x кратен шести, и в этом
случае f (x) = w(i). Видно, что знаменатель всегда одинаков для любых x
отличающихся на 6:
| x | Знаменатель |
| 1 + 6n | |
| 2 + 6n | |
| 3 + 6n | |
| 4 + 6n | |
| 5 + 6n | |
n 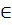 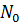
|
Ява апплет построения графика временнóй волны доступен на сайте
www.timewave2012.com
|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!