Теорема 4. Если в индексной строке симплексной таблицы ЗЛП на максимум (минимум) содержится отрицательная (положительная) оценка  , а в соответствующем столбце переменной
, а в соответствующем столбце переменной 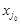 нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху (снизу). Задача неразрешима.
нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху (снизу). Задача неразрешима.
С экономической точки зрения неограниченность целевой функции ЗЛП свидетельствует только об одном: разработанная модель недостаточно точна.
Пример 2. Решить симплексным методом задачу

Решение
Упорядочим запись исходной задачи. Так как в первом неравенстве системы ограничений свободный член отрицателен, то умножим первое неравенство на –1. В результате получим

Ограничения-неравенства имеют вид £, следовательно, целевая функция должна быть на максимум. В нашем случае задачу на минимум можно заменить задачей максимизации. Умножив целевую функцию на –1, получаем

Итак, запишем задачу в каноническом виде. Для этого добавим к левым частям неравенств дополнительные переменные x 3, x 4, x 5. В целевую функцию они сводятся с коэффициентами, равными нулю:

Задача имеет предпочтительный вид.
Переменные x 3, x 4, x 5 – базисные, а x 1, x 2 – свободные. Положим, что x 1 = x 2 = 0, тогда x 3 = 14, x 4 = 3, x 5 = 36. Следовательно, x 0 = (0; 0; 14; 3; 36) является начальным опорным планом.
При этом  6 × 0 + 3 × 0 + 0 × 14 + 0 × 3 + 0 × 36 = 0. Заносим условие задачи в симплексную табл. 2.
6 × 0 + 3 × 0 + 0 × 14 + 0 × 3 + 0 × 36 = 0. Заносим условие задачи в симплексную табл. 2.
Таблица 2
| БП
| сБ
| А 0
| x 1
| x 2
| x 3
| x 4
| x 5
|
|
|
|
|
|
|
|
|
| x 3
|
|
| (2)
|
|
|
|
| 
|
| x 4
|
|
|
|
|
|
|
|
|
| x 5
|
|
|
|
|
|
|
|
|

|
| –6
| –3
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
Наличие в индексной строке ( -строке) отрицательных оценок при решении задачи на максимум свидетельствует о том, что оптимальное решение не получено. От табл. 2 перейдем к табл. 3.
-строке) отрицательных оценок при решении задачи на максимум свидетельствует о том, что оптимальное решение не получено. От табл. 2 перейдем к табл. 3.
Таблица 3
| БП
| сБ
| А 0
| x 1
| x 2
| x 3
| x 4
| x 5
|
|
|
|
|
|
|
| x 1
|
|
|
| 
| 
|
|
|
| x 4
|
|
|
|
|
|
|
|
| x 5
|
|
|
| –5
| –2
|
|
|

|
|
|
|
|
|
|
Разрешающий столбец находим по max{|–6|; |–3|} = 6. Разрешающая строка определяется по минимуму отношений свободных членов к положительным элементам разрешающего столбца, т. е.
 .
.
На пересечении разрешающего столбца и разрешающей строки находится разрешающий элемент 2.
В табл. 3 вместо x 3 в базис вводим переменную x 1.
В новой таблице на месте разрешающего элемента пишем 1, все остальные элементы разрешающего столбца – нули, элементы разрешающей строки делятся на разрешающий элемент. Все остальные элементы табл. 3 вычисляются по правилу прямоугольника.
В индексной строке табл. 3 нет отрицательных элементов. Следовательно, мы получаем оптимальный план x * = хопт = (7; 0; 0; 3; 8). Тогда  = z (хопт) = 42, z min = z (хопт) = –42.
= z (хопт) = 42, z min = z (хопт) = –42.
Ответ: хопт = (7; 0; 0; 3; 8), z min = –42.
Пример 3. Решить задачу

Решение
Сведем задачу к каноническому виду. Получим

Занесем условие в симплексную табл. 4. Начальный опорный план имеет вид x 0 = (0; 0; 3; 10), z (x 0) = 0.
Таблица 4
| БП
| сБ
| А 0
| x 1
| x 2
| x 3
| x 4
|
|
|
|
|
|
| x 3
|
|
| –1
|
|
|
|
| x 4
|
|
|
|
|
|
|
| zj – cj
|
| –2
| –1
|
|
|
|
|
|
| 
|
|
|
|
Задача решается на максимум. Опорный план x 0 неоптимальный, так как существуют отрицательные оценки. Находим разрешающий столбец по max{|–2|, |–1|} = 2.
Итак, в базис нужно вводить переменную x 1, но все элементы разрешающего столбца неположительны. Следовательно, по теореме 4 (признак неограниченности целевой функции) целевая функция на множестве допустимых планов не ограничена сверху, т. е.  .
.
Ответ:  .
.
2.9. Метод искусственного базиса (М-задача)
Решение задачи линейного программирования симплекс-методом начинается с нахождения какого-либо опорного плана.
Рассмотрим третий случай построения начального опорного плана (первый и второй описаны в пункте 2.1).
Пусть система ограничений имеет вид
 .
.
Перейдем к каноническому виду путем введения дополнительных переменных  , которые вычитаем из левых частей неравенств системы. Получим систему
, которые вычитаем из левых частей неравенств системы. Получим систему
 .
.
Теперь система ограничений не имеет предпочтительного вида, так как дополнительные переменные xn + i входят в левую часть (при bi  0) с коэффициентами, равными –1. В этом случае вводится так называемый искусственный базис путем перехода к М-задаче.
0) с коэффициентами, равными –1. В этом случае вводится так называемый искусственный базис путем перехода к М-задаче.
К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные wi. В целевую функцию переменные wi вводят с коэффициентом M в случае решения задачи на минимум и с коэффициентом – M – для задачи на максимум, где M – большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
Пусть исходная задача линейного программирования имеет вид
При этом ни одно из ограничений не имеет предпочтительной переменной. М-задача будет записываться следующим образом:
При этом знак “–” в функции (10) относится к задаче на максимум. Задача (10)–(12) имеет предпочтительный вид. Ее начальный опорный план имеет вид
 .
.
Если некоторые из уравнений (8) имеют предпочтительный вид, то в них не следует вводить искусственные переменные.
Теорема 5. Если в оптимальном плане хопт = 
 М -задачи (10)–(12) все искусственные переменные
М -задачи (10)–(12) все искусственные переменные  , то план
, то план  является оптимальным планом исходной задачи (7)–(9).
является оптимальным планом исходной задачи (7)–(9).
Теорема 6 (признак несовместности системы ограничений). Если в оптимальном плане М -задачи хотя бы одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна.
В случае М -задачи индексную строку симплексной таблицы разбиваем на две. В первой строке записываются свободные члены выражений  и
и  , а во второй – коэффициенты, содержащие М. Признак оптимальности проверяется сначала по второй строке. По ней же определяется переменная, подлежащая включению в базис. По мере исключения из базиса искусственных переменных соответствующие им столбцы элементов можно опускать. Объясняется это тем, что искусственные переменные в базис не возвращают, а поэтому отвечающие им столбцы больше не потребуются. После исключения из базиса всех искусственных переменных процесс отыскания оптимального плана продолжают с использованием первой строки целевой функции.
, а во второй – коэффициенты, содержащие М. Признак оптимальности проверяется сначала по второй строке. По ней же определяется переменная, подлежащая включению в базис. По мере исключения из базиса искусственных переменных соответствующие им столбцы элементов можно опускать. Объясняется это тем, что искусственные переменные в базис не возвращают, а поэтому отвечающие им столбцы больше не потребуются. После исключения из базиса всех искусственных переменных процесс отыскания оптимального плана продолжают с использованием первой строки целевой функции.
Пример 4. Решить с использованием искусственного базиса задачу линейного программирования


Решение
Сведем задачу к каноническому виду. Получим

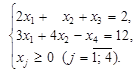
Первое ограничение имеет предпочтительную переменную х 3, а второе – нет. Поэтому вводим в него искусственную переменную w 1. Приходим к М- задаче


Занесем условие М- задачи в симплексную табл. 5. Начальный опорный план имеет вид x 0 = (x 1; x 2; x 3; x 4; w 1) = (0; 0; 2; 0; 12), z (x 0) = 0 – 12 M.
Таблица 5
| БП
| сБ
| А 0
| x 1
| x 2
| x 3
| x 4
| w 1
|
|
|
|
|
|
| – M
|
|
| x 3
|
|
|
| (1)
|
|
|
| 
|
| w 1
| – M
|
|
|
|
| –1
|
|
|
| zj – cj
|
| –6
| –4
|
|
|
|
|
| –12 M
| –3 M
| –4 M
|
| M
|
|
|
|
|
|
|
| 
|
|
|
|
|
| | | | | | | | | | |
Сделаем необходимые пояснения.
Индексную строку удобно разбить на две. В первой из них записываются свободные члены выражений D0 = cБ × А 0 и D j = cБ × Aj – cj, а во второй – коэффициенты, содержащие M. Например, для табл. 5:



Признак оптимальности проверяем сначала по второй строке индексной строки. Так как в ней существуют отрицательные оценки, то план x 0 не является оптимальным.
Переходим к новой табл. 6.
Разрешающий столбец находим по max{|–3 M |; |–4 M |} = 4 M, разрешающая строка определяется по  . Следовательно, 1 – разрешающий элемент.
. Следовательно, 1 – разрешающий элемент.
Таблица 6
| БП
| сБ
| А 0
| x 1
| x 2
| x 3
| x 4
| w 1
|
|
|
|
|
| – M
|
| x 2
|
|
|
|
|
|
|
|
| w 1
| – M
|
| –5
|
| –4
| –1
|
|
| zj – cj
|
|
|
|
|
|
|
| –4 M
| 5 M
|
| 4 M
| M
|
|
В индексной строке нет отрицательных оценок. Следовательно, по признаку оптимальности опорный план (0; 2; 0; 0; 4) оптимален. Но так как в оптимальном плане искусственная переменная w 1 не равна 0, то по теореме 6 система ограничений исходной задачи несовместна. Задача решения не имеет.
Ответ:нет решения.
Пример 5. Решить с использованием искусственного базиса задачу


Решение
Упорядочим запись исходной задачи. Умножим второе неравенство на –1:


Сведем задачу к каноническому виду. Получим
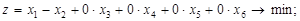

Первое и четвертое ограничения имеют предпочтительные переменные, а второе и третье – нет. Поэтому вводим в них искусственные переменные w 1 и w 2. Приходим к М- задаче


Занесем условие М- задачи в симплексную табл. 7. Начальный опорный план имеет вид x 0 = (0; 0; 10; 0; 0; 4; 3; 9), z (x 0) = 0 + 12 M.
Таблица 7
| БП
| сБ
| А 0
| x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| w 1
| w 2
|
|
|
| –1
|
|
|
|
| M
| M
|
|
| x 3
|
|
|
|
|
|
|
|
|
|
|
|
| w 1
| M
|
| (1)
| –3
|
| –1
|
|
|
|
| 
|
| w 2
| M
|
|
|
|
|
| –1
|
|
|
|
|
| х 6
|
|
| –1
|
|
|
|
|
|
|
|
|
| zj – cj
|
| –1
|
|
|
|
|
|
|
|
|
| 12 M
| 4 M
| –2 M
|
| – M
| – M
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
Мы решаем задачу на минимум. Признак оптимальности проверяем сначала по второй строке индексной строки. Так как в ней существует положительная оценка, то план x 0 не является оптимальным. Переходим к новой табл. 8.
Таблица 8
| БП
| сБ
| А 0
| x 1
| x 2
| x 3
| x 4
| x 5
| x 6
| w 2
|
|
|
| –1
|
|
|
|
| M
|
|
| x 3
|
|
|
|
|
|
|
|
|
|
|
| x 1
|
|
|
| –3
|
| –1
|
|
|
|
|
| w 2
| M
|
|
| (10)
|
|
| –1
|
|
| 
|
| x 6
|
|
|
| –2
|
| –1
|
|
|
|
|
| zj – cj
|
|
| –2
|
| –1
|
|
|
|
|
|
|
| 10 M
|
| 3 M
| – M
|
|
|
|
|
|
|
|
| 
|
|
|
|
|
| |
| | | | | | | | | | | | |
По мере вывода из базиса искусственных переменных соответствующие им столбцы можно опускать. Разрешающий столбец находим по max{4 M } = 4 M, разрешающая строка определяется по  . Следовательно, 1 – разрешающий элемент.
. Следовательно, 1 – разрешающий элемент.
Так как существуют положительные оценки, то план x 1 = (3; 0; 7; 0; 0; 7; 0; 0) не является оптимальным.
Переходим к табл. 9. Разрешающий столбец находим по max{10 M; 3 M } = 10 M, разрешающая строка определяется по  .
.
Итак, 10 – разрешающий элемент.
Таблица 9
| БП
| сБ
| А 0
| x 1
| x 2
| х 3
| x 4
| x 5
| x 6
|
|
| –1
|
|
|
|
|
| x 3
|
|
|
|
|
| 
| 
|
|
| x 1
|
|
|
|
|
| 
| 
|
|
| x 2
| –1
|
|
|
|
| 
| 
|
|
| x 6
|
|
|
|
|
| 
| 
|
|
| zj – cj
|
|
|
|
| 
| 
|
|
Так как все оценки неположительны, то получен оптимальный план. Итак, x * = хопт = (3; 0; 7; 0; 0; 7), z min = (x *) = 3.
Ответ: хопт = (3; 0; 7; 0; 0; 7), z min = 3.
Вопросы для самоконтроля
1. Суть симплекс-метода. Свойства задач линейного программирования, на которых он основан.
2. Последовательность этапов практической реализации алгоритма симплекс-метода при решении задач линейного программирования.
3. Построение начального опорного плана (3 случая).
4. Случаи, когда опорный план оптимален.
5. Переход к нехудшему опорному плану.
6. Симплексные преобразования.
7. Признак бесконечности множества оптимальных планов.
8. Понятие о вырождении. Монотонность и конечность симплексного метода. Зацикливание.
9. Признак неограниченности целевой функции.
10. Необходимость использования симплекс-метода с искусственным базисом (М -метода). Суть этой модификации симплекс-метода.
11. Определение искусственной переменной. Случаи, при которых она вводится. Коэффициент, соответствующий ей в линейной функции. Проведение анализа плана по индексной строке.
12. Признак несовместности системы ограничений.



 , а в соответствующем столбце переменной
, а в соответствующем столбце переменной 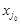 нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху (снизу). Задача неразрешима.
нет ни одного положительного элемента, то целевая функция на множестве допустимых планов задачи не ограничена сверху (снизу). Задача неразрешима.



 6 × 0 + 3 × 0 + 0 × 14 + 0 × 3 + 0 × 36 = 0. Заносим условие задачи в симплексную табл. 2.
6 × 0 + 3 × 0 + 0 × 14 + 0 × 3 + 0 × 36 = 0. Заносим условие задачи в симплексную табл. 2.


 -строке) отрицательных оценок при решении задачи на максимум свидетельствует о том, что оптимальное решение не получено. От табл. 2 перейдем к табл. 3.
-строке) отрицательных оценок при решении задачи на максимум свидетельствует о том, что оптимальное решение не получено. От табл. 2 перейдем к табл. 3.


 .
. = z (хопт) = 42, z min = z (хопт) = –42.
= z (хопт) = 42, z min = z (хопт) = –42.

 .
. .
. , которые вычитаем из левых частей неравенств системы. Получим систему
, которые вычитаем из левых частей неравенств системы. Получим систему .
. 0) с коэффициентами, равными –1. В этом случае вводится так называемый искусственный базис путем перехода к М-задаче.
0) с коэффициентами, равными –1. В этом случае вводится так называемый искусственный базис путем перехода к М-задаче. ;
;

 ;
;

 ;
;



 .
.
 М -задачи (10)–(12) все искусственные переменные
М -задачи (10)–(12) все искусственные переменные  , то план
, то план  является оптимальным планом исходной задачи (7)–(9).
является оптимальным планом исходной задачи (7)–(9). и
и  , а во второй – коэффициенты, содержащие М. Признак оптимальности проверяется сначала по второй строке. По ней же определяется переменная, подлежащая включению в базис. По мере исключения из базиса искусственных переменных соответствующие им столбцы элементов можно опускать. Объясняется это тем, что искусственные переменные в базис не возвращают, а поэтому отвечающие им столбцы больше не потребуются. После исключения из базиса всех искусственных переменных процесс отыскания оптимального плана продолжают с использованием первой строки целевой функции.
, а во второй – коэффициенты, содержащие М. Признак оптимальности проверяется сначала по второй строке. По ней же определяется переменная, подлежащая включению в базис. По мере исключения из базиса искусственных переменных соответствующие им столбцы элементов можно опускать. Объясняется это тем, что искусственные переменные в базис не возвращают, а поэтому отвечающие им столбцы больше не потребуются. После исключения из базиса всех искусственных переменных процесс отыскания оптимального плана продолжают с использованием первой строки целевой функции.


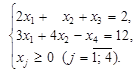





 . Следовательно, 1 – разрешающий элемент.
. Следовательно, 1 – разрешающий элемент.


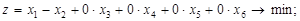



 . Следовательно, 1 – разрешающий элемент.
. Следовательно, 1 – разрешающий элемент. .
.








