

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
Топ:
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Частные производные.
Задача 1. Найти частные производные от функций:
а)  .
.
Решение. Частную производную  находим как производную функции
находим как производную функции  по аргументу
по аргументу  в предположении, что
в предположении, что  . Поэтому,
. Поэтому,

Аналогично,

б) 


в) 


г) 


Пример 2
 . Показать, что
. Показать, что  .
.





Пример 3
 . Показать, что
. Показать, что  .
.






Производная сложной функции. Производная неявной функции
Задача 1. Продифференцировать сложную функцию:
а) 
Решение. Так как  и
и  зависят от переменных
зависят от переменных  и
и  , то функция
, то функция  в конечном итоге зависит от переменных
в конечном итоге зависит от переменных  и
и  , и ее частные производные можно найти по формулам:
, и ее частные производные можно найти по формулам:


Следовательно,


б)  Найти
Найти 
Решение. Так как функция  в конечном итоге зависит от одной переменной
в конечном итоге зависит от одной переменной  , то ее производную можно найти по формуле:
, то ее производную можно найти по формуле:
 Тогда,
Тогда, 

Экстремум функции
Дана функция  .
.
а) исследовать функцию на экстремум;
Решение. а) Найдем стационарные точки функции из системы уравнений: 


 Следовательно,
Следовательно,
Точка  - стационарная точка функции. Вычислим значения частных производных второго порядка в точке
- стационарная точка функции. Вычислим значения частных производных второго порядка в точке  .
.

Составим дискриминант  . Так как
. Так как  , то экстремум есть, так как
, то экстремум есть, так как  , то
, то  - точка минимума.
- точка минимума.
Наименьшее и наибольшее значение функции в замкнутой области
Задание 1 Дана функция  .
.
найти наибольшее и наименьшее значения функции в замкнутой области  , заданной системой неравенств
, заданной системой неравенств  , сделать чертеж области.
, сделать чертеж области.
Решение. а) Найдем стационарные точки функции из системы уравнений: 


 Следовательно,
Следовательно,
Точка  - стационарная точка функции. Вычислим значения частных производных второго порядка в точке
- стационарная точка функции. Вычислим значения частных производных второго порядка в точке  .
.

Составим дискриминант  . Так как
. Так как  , то экстремум есть, так как
, то экстремум есть, так как  , то
, то  - точка минимума.
- точка минимума.
б) Построим область  , заданную системой неравенств
, заданную системой неравенств  .
.

Это треугольник с вершинами в точках О(0;0), А(-3;0), В(0;-3).
|
|
Наибольшее и наименьшее значения в замкнутой области  функция
функция  может достигать в стационарных точках, принадлежащих области
может достигать в стационарных точках, принадлежащих области  и на границе области. Поэтому:
и на границе области. Поэтому:
Вычислим значение функции в стационарной точке  , принадлежащей области
, принадлежащей области  :
:  .
.
Вычислим значения функции в точках О(0;0), А(-3;0), В(0;-3), которые являются точками «стыковки» различных участков границы области. 


Вычислим значения функции в критических точках на границе области.
I участок: 

 - критическая точка, принадлежащая [-3;0].
- критическая точка, принадлежащая [-3;0]. 
II участок: 

 - критическая точка, принадлежащая [-3;0].
- критическая точка, принадлежащая [-3;0]. 
III участок: 
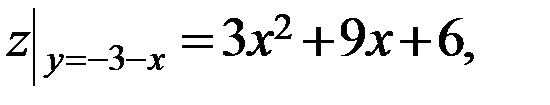
 - критическая точка, принадлежащая [-3;0].
- критическая точка, принадлежащая [-3;0]. 
Из всех вычисленных значений выберем наибольшее и наименьшее:  в точках
в точках  ,
,  -1 в точке
-1 в точке  .
.
Задание 2 Дана функция  , точка
, точка 
 и вектор
и вектор  .
.
Найти производную по направлению вектора  в точке
в точке  и
и  .
.
Решение: Найдем направляющие косинусы вектора  :
:

 .
.
Далее находим значения частных производных от функции в точке  :
:


Наконец, вычисляем производную по направлению  в точке
в точке  и градиент:
и градиент:
 ,
,
 .
.
Задание 3. Дана функция  , точка
, точка  и вектор
и вектор  . Найти: производную по направлению вектора
. Найти: производную по направлению вектора  в точке
в точке  ;
;  в этой точке.
в этой точке.
Решение.
1.Для решение задачи воспользуемся формулой для нахождения производной от функции 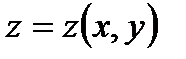 в заданной точке
в заданной точке 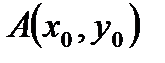 по направлению вектора
по направлению вектора  :
:
 ,
,
где  ,
,  - направляющие косинусы вектора
- направляющие косинусы вектора  , которые вычисляются по формулам:
, которые вычисляются по формулам:  ,
,  .
.
По условиям задачи вектор  имеет координаты
имеет координаты  ,
,  . Тогда его длина равна:
. Тогда его длина равна: 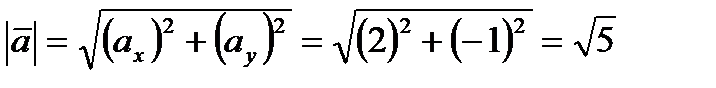 .
.
Следовательно, для направляющих косинусов вектора получим следующие значения:  ,
, 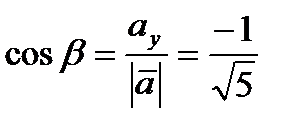 .
.
Для решения задачи необходимо найти все частные производные первого порядка от функции  :
:


Вычислим значения этих частных производных первого порядка в точке 


В заключении подставим полученные значения для направляющих косинусов вектора  и значения частных производных первого порядка от функции z в точке
и значения частных производных первого порядка от функции z в точке  в формулу производной по направлению в заданной точке:
в формулу производной по направлению в заданной точке:

2. 
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!