Язык Си с помощью оператора typedef позволяет задавать новое имя уже существующим переменным. При этом не создается новый тип данных.
Например:
typedef char SIMBOL;
typedef unsigned UNSIGN;
typedef float real;
Достаточно часто используется оператор typedef с применением структур:
typedef struct st_tag {
char name[30];
int kurs;
char group[3];
int stip;
} STUDENT;
Теперь для определения переменной можно использовать
struct st_tag avar;
а можно использовать
STUDENT avar;
Выделение памяти и управление ею
Определение размера выделяемой памяти (операция sizeof)
С помощью этой операции можно определить в байтах размер памяти, которая соответствует идентификатору или типу. Выражение с операцией sizeof имеет следующий формат
sizeof (выражение)
Выражение - это либо идентификатор, либо имя типа, заключенное в круглые скобки:
sizeof (имя_объекта);
Идентификатор не может относиться к полю битов или быть именем функции.
Если имя типа описывает массив, то результатом является размер всего массива, а не размер указателя, состветствующий имени массива.
Пример 7.1:
# include <stdio. h>
# include <conio. h>
void main (void)
{
float mas[100];
clrscr();
printf(“Размер одного элемента массива %d в байтах\n, sizeof (mas[20]));
printf(“Размер всего массива %d в байтах\n, sizeof (mas));
getch();
}
Результат выполнения программы:
Размер одного элемента массива 4 байта.
Размер всего массива 400 байт.
Динамическое выделение памяти
Язык Си позволяет выделять память динамически, т.е. во время работы программы. Как было показано ранее, по области видимости переменные могут быть глобальными и локальными. Для глобальных переменных отводится фиксированная часть памяти на все время работы программы. Локальные переменные хранятся в стеке. Между ними находится область свободной памяти для динамического распределения во время работы программы. Принятое распределение памяти в программах на языке Си показано на рис.7.1.
______________________
| |
Область стека старшие адреса
(заполнять сверху вниз)
_______________________
| |
Свободная область
памяти
_______________________
| Раздел глобальных |
переменных и
констант
_______________________
| |
Область программного
кода младшие адреса
|_______________________|
Рис.7.1
Наиболее важными функциями для динамического распределения памяти являются malloc() и free(). Прототипы этих функций хранятся в заголовочном файле alloc.h
Выделение памяти размером size байт осуществляется функцией malloc().
Синтаксис использования:
unsigned size; / * размер блока памяти в байтах */
void *malloc (size);
void free(void *p);
Функция malloc() возвращает указатель на первый байт выделенного блока памяти либо NULL, если для выделения памяти указанного размера нет места.
Действие функции free(), обратное действию функции malloc(). Эта функция освобождает ранее выделенную область памяти.
Выделение памяти и ее обнуление осуществляется функцией calloc().
Синтаксис:
unsigned n_elem, size_elem; /* число элементов и размер одного элемента в байтах */
void *calloc (n_ elem, size_elem);
Функция возвращает указатель на выделенный блок памяти, либо
NULL, если память нельзя выделить.
Из приведенных описаний видно, что обе функции возвращают указатель на любой тип (void), следовательно, при обращении к этим функциям необходимо использовать явную операцию преобразования типов.
Освобождение ранее выделенной памяти осуществляется функцией
void free (ptr):
char *ptr;
ptr = (char*) malloc(…);
…
free (ptr);
Пример 7.2: Выделение памяти под массивы
# include<alloc.h>
# include<stdio.h>
# include<conio.h>
# include<stdlib.h>
int main (void)
{
int *mas_1;
float *mas_2;
clrscr ();
mas_1 = (int*)malloc(10*sizeof (int));
mas_2 = (float*)calloc(1000,sizeof(float));
uf (mas_1==NULL || mas_2== NULL)
{
printf (“Не хватает памяти ”);
getch ();
exit (0);
}
printf(“Начало mas_1 %p\n”,mas_1);
printf(“Начало mas_2 %p\n”,mas_2);
getch ();
free (mas_1);
free (mas_2);
return (1);
}
В С++ для выделения и освобождения памяти используется также функции new() и delete ().
Динамическое распределение памяти удобно использовать тогда, когда заранее неизвестно количество используемых переменных. В частности, этот механизм используется для создания массивов с изменяемым количеством элементов.
Динамические массивы
При работе с массивами память для размещения их элементов может выделяться динамически. Для одномерных массивов доступ к элементам осуществляется как обычно: по номеру индекса элементов.
В случае использования двумерных массивов (матриц) их элементы располагаются в памяти в виде линейного массива. При этом доступ к отдельному элементу осуществляется не по номеру строки и столбца, а также как и для одномерных массивов - по номеру элемента. Таким образом, программист сам должен контролировать правильность доступа к нужному элементу массива.
Чтобы работать с матрицами в естественной форме, целесообразно выделять память с использованием двойных указателей. Рассмотрим фрагмент программы:
a = (int**) malloc(m*sizeof (int*));
for (i = 0: i <m; i++)
a[i] = (int*)malloc(n*sizeof (int));
В результате выполнения первой строки будет выделена память для размещения m указателей на данное типа int, а переменной а будет присвоено значение адреса начала выделенной области. В результате выполнения цикла for будет выделена память для размещения m*n элементов типа int в соответствии со следующей схемой:
1-й этап 2-й этап (цикл for)
int **a -> int*a[0] ->a[0] [0] a[0] [1] a[0] [2] … a[0] [n]
int* a[1] -> a[1] [0] a[1] [1] a[1] [2] … a[1] [n]
int* a[2] -> a[2] [0] a[2] [1] a[2] [2] … a[2] [n]
…
int* a[m] -> a[m][0] a[m][1] a[m][2] …a[m] [n]
Таким образом, в памяти будет выделена область для размещения элементов матрицы размером m*n, а доступ к отдельному элементу будет осуществляться по индексу строки и столбца.
Пример 7.3: Работа с динамическими массивами
#include<stdio.h>
#include<conio.h>
#include<alloc.h>
int** input (int, int); //Функция ввода матрицы
void output (int**, int, int); // Функция вывода матрицы
void making (int**, int, int);
void main(void)
{
int m,n;
int** p;
clrscr();
puts(“Введите размер исходной матрицы “);
printf(“число строк = “);
scant(“%d”,&m);
printf(“число столбцов = “);
scanf(“%d”,&n);
p = input(m,n);
making(p,m,n);
output (p,m,n);
free(p);
getch();
}
int** input(int m, int n)
{
int i, j;
int **a;
a=(int**)malloc(m*sizeof(int*));
for(i=0; i<m; i++)
{
a[i]=(int*)malloc(n*sizeof(int));
for(j=0; j<n; j++)
{
a[i] [j] =0;
}
}
for(i=0; i<m; i++)
for(j=0; j<n; j++)
{
printf(“\nВведите А(%1d,%1d) элемент матрицы: “, i+1, j+1);
scanf(“%d”, &a[i] [j]);
}
return a;
}
/*Функция заменяет элементы с четной суммой индексов на противоположные */
void making(int **a, int m, int n)
{
int i, j;
for (i=0; i<m; i++)
for(j=0; j<n; j++)
if((i=j)%2 = = 0)
a[i] [j] = -a[i] [j];
}
void output(int **z, int m, int n)
{
int i,j;
printf(“\nРезультирующая матрица \n”);
for(i=0; i<m; i++)
{
for(j=0; j<n; j++)
printf(“%8d”, z[i] [j]);
printf(“\n”);
}
}
Динамические структуры
Каждая структура данных характеризуется, во – первых, взаимосвязью элементов и, во-вторых, набором типовых операций над этой структурой. В случае динамической структуры важно знать:
1) каким образом может расти и сокращаться структура данных;
2) каким образом можно включить в структуру новый элемент и удалить существующий;
3) как можно обратиться к конкретному элементу структуры для выполнения над ним определенной операции.
Доступ по индексу, как это осуществляется в массивах, здесь не удобен, так как любой элемент при изменении размеров структуры может изменить свою позицию. Поэтому доступ к элементам динамической структуры относительный: найти следующий (предыдущий) элемент по отношению к текущему, найти последний элемент и т.д.
Одной из простейших и в то же время типичных динамических структур данных является очередь. Проблема очереди возникает всегда, когда имеется некоторый механизм обслуживания, который может выполнять заказы последовательно, один за другим. Если к моменту поступления нового заказа данное устройство свободно, оно немедленно приступает к выполнения заказа. Если же оно занято, то заказ поступает в конец очереди других заказов. Когда устройство освободится, оно приступает к выполнению заказа из начала очереди. Если заказы поступают нерегулярно, очередь то удлиняется, то укорачивается и даже может оказаться пустой (рис 7.2).




12
Рис.7.2
Очередь часто называют системой, организованной и работающей по принципу FIFO (first in – first out). Основными операциями с очередью являются добавление нового элемента в конец и удаление элемента из начала очереди.
Рассмотрим, как может быть реализована работа с очередью на Си с использованием структур, указателей на структуры и функции динамического выделения/освобождения памяти.
В программе, приведённой ниже, работа с очередью ведётся с помощью двух функций:
Функция insert() отводит память под очередной элемент, заносит в него нужную информацию и ставит в конец очереди.
Функция take_off() удаляет из очереди её первый элемент, освобождает память из-под него и перемещает указатель начала очереди на следующий элемент.
В случае попытки удаления элемента из пустой очереди параметр ошибки error получает значение 1.
#include <studio.h>
#include <alloc.h>
#define QUEUE struct queue
QUEUE
{ int info; // поле информации элемента очереди
QUEUE * next; // поле ссылки на следующий элемент очереди
};
void insert (QUEUE **q, int item)
{
QUEUE *tek = * q; // указатель на текущее звено очереди
QUEUE *pred = 0; // pred содержит адрес последнего элемента
QUEUE *new_n;
while(tek) //просматриваем очередь до конца
{ pred=tek; tek= tekànext;}
new_nàinfo=item;
if(pred) //очередь не пуста
{new_nànext=predànext;
predànext=new_n;
}
else { q=new_n;(*q) ànext=0;}
}
int take_off(QUEUE **q, int *error)
{int value=0; //значение возвращаемого элемента очереди
QUEUE *old= *q; //указатель на старую голову очереди
if(*q) //если очередь не пуста
{value=oldàinfo; q=(*q)ànext;
free(old); *error=0; //элемент удален из очереди
}
else *error=1;
return value;
}
void main(void)
{
int error, j;
QUEUE*q1, q2;
for(j=12;j<=15;j++)
insert(&q1,j);
for(j=1;j<=4;j++)
insert(&q2,take_off(&q1,&error));
for(j=1;j<=4;j++)
printf(“\n q2:%d”, take_off(&q2,&error));
}
Другая часто встречающаяся структура данных - стек (магазин)- отличается от очереди тем, что она организована по принципу LIFO (last in – first out). Операции включения и удаления элемента в стеке выполняются только с одного конца, называемого вершиной стека. Когда новый элемент помещается в стек, то прежний верхний элемент как бы “проталкивается” вниз и становится временно недоступным. Когда же верхний элемент удаляется c вершины стека, предыдущий элемент “выталкивается” наверх и опять является доступным (рис.7.3).



 45 45
45 45
Рис. 7.3
 Потребность в организации стека возникает при решении, например, такой задачи. Пусть имеется текст, сбалансированный по круглым скобкам.
Потребность в организации стека возникает при решении, например, такой задачи. Пусть имеется текст, сбалансированный по круглым скобкам.
Необходимо построить таблицу, в каждой строке которой будут находиться
координаты соответствующих пар скобок, т.е. для текста
(….(…….)….(…… ……)……..)
0 17 42 61 84 95
таблица должна быть такой
17 42
61 84
0 95
Поскольку текст сбалансирован по круглым скобкам, то как только встретится “)”, это будет пара для последней пройденной “(“.
Поэтому алгоритм решения данной задачи может быть следующим: будем идти по тексту и как только встретим “(“, занесем её координату в стек; как только встретится “)”, возьмём из стёка верхнюю координату и распечатаем её вместе с координатой данной ”)”.
Рассмотрим программу, в которой реализована работа со стеком. В ней использованы функции:
push() – положить элемент на вершину стека,
pop() – вытолкнуть верхний элемент из стёка,
peek() – прочитать значение верхнего элемента, не удаляя сам элемент из стека.
#include<stdio.h>
#include<alloc.h>
#define STACK struct stack
STACK
{ nt info; //поле значения элемента стека
STACK *next; //поле ссылки на следующий элемент стека
};
void push (STACK **s, int item)
{
STACK *new_n;
new_n=(STACK*) malloc(sizeof(STACK));//запросили память под
//новый элемент
new_n-->info=item; //заносим значение в новый элемент
new_n-->next=*s; //новый элемент стал головой стёка
*s=new_n; //указателю *s присвоили адрес головы стёка
}
int pop(STACK **s, int *error)
{
STACK *old =* s;
int info=0;
if(*s) //стек не пуст
{ info=old-->info; s=(*s)->next;
free(old); //освобождаем память из-под выбранного элемента
*error =0; // элемент удален успешно
}
else *error=1;
return (info);
}
int peek (STACK **s, int *error)
{
if (*s) {*error=0; return (*s) --> info; }
else { *error=1; return 0; }
}
void main()
{
int error, i;
STACK *sl, *s2;
push (&s1, 42);
printf (“ \ n peek (s1)= % d “, peek (&s1, & error));
push (&s1, 53);
printf (“\ n peek (s1)=% d “, peek (&s1, & error));
push (&s1, 72);
printf (“\n peek (s1) = %d”, peek (&s1, & error));
push (&s1, 86);
printf (“\n peek (s1)=%d”, peek (&s1, &error));
for (i=1; i<=4; i ++)
push (&s2, pop(&s1, &error));
for (i=1; i<= 4; i ++)
printf (“\n pop(&s2)=%d”, pop(&s2, &error));
}
Стеки и очереди являются одними из разновидностей более широкого класса структур данных – списков. Связанный список – это структура следующего вида (рис.7.4)


 …….
…….
Рис.7.4
Это простой однонаправленный список, в котором каждый элемент, кроме последнего, имеет ссылку на следующий элемент и поле информации. Можно организовать также кольцевой список (в нём последний элемент будет содержать ссылку на первый) или двунаправленный список (когда каждый элемент, кроме первого и последнего, имеет две ссылки: на предыдущий и следующий элемент) и т.д. (рис. 7.5). Кроме того, можно поместить в начале списка дополнительный элемент, называемый заголовком списка. Как правило, заголовок списка используется для хранения информации обо всём списке. В частности, он может содержать счётчик числа элементов в списке. Наличие заголовка приводит к усложнению одних и упрощению других программ, работающих со списками.












Рис.7.5
При работе со списком могут быть полезны следующие базовые функции:
insert() – добавить новый элемент в список таким образом, чтобы список оставался упорядоченным в порядке возрастания по значению одного из полей;
take_out() – удалить элемент с заданным полем (если он есть в списке);
is_ present() – определить, имеется ли в списке заданный элемент;
displey() – распечатать значения всех полей элементов списка;
destroy_list() – освободить память, занимаемую списком.
Довольно часто при работе с данными бывает удобно использовать структуру с иерархическим представлением, которые хорошо изображаются с помощью дерева (рис.7.6).







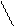











Рис.7.6
Дерево состоит из элементов называемых узлами (вершинами). Узлы соединены между собой направленными дугами. В случае X --> Y вершина X называется предшественником (родителем), а Y – приемником (сыном). Дерево имеет единственный узел - корень, у которого нет предшественников. Любой другой узел имеет ровно одного предшественника. Узел, не имеющий приемника, называется листом.
Рассмотрим работу с бинарным деревом (в котором у каждого узла может быть только два преемника: левый и правый сын). Необходимо уметь:
- построить дерево;
- выполнить поиск элемента с указанным значением в узле;
- удалить заданный элемент;
- обойти все элементы дерева (например, чтобы над каждым из них провести некоторую операцию).
Обычно бинарное дерево строится сразу упорядоченным, т. е. узел левого сына имеет значение меньше, чем значение родителя, а узел правого сына - большее. Например, если приходят числа 17,18,6,5,9,23,12,7,8, то построенное по ним дерево будет выглядеть так как это представлено на рис.7.6.


 6
6

 5 9 23
5 9 23
 7 12
7 12
Рис.7.6
Для того, чтобы вставить новый элемент в дерево, надо найти для него место. Для этого, начиная с корня, будем сравнивать значения узлов (Y) со значением нового элемента (NEW). Если NEW<Y, то пойдём по левой ветви; в противном случае - по правой ветви. Когда дойдём до узла, из которого не выходит нужная ветвь для дальнейшего поиска, это означает, что место под новый элемент найдено. Путь поиска места для числа 11 в построенном выше дереве показан на рис.7.7
При удалении узла из дерева возможны три ситуации:
- исключаемый узел – лист (в этом случае надо просто удалить ссылку на данный узел);
- из исключаемого узла выходит только одна ветвь;

 17
17
6 

 18
18
5 9

 23
23
7 12
8 11
Рис.7.7
- из исключаемого узла выходят две ветви (в таком случае на место удаляемого узла надо поставить либо самый правый узел левой ветви, либо самый левый узел правой ветви для сохранения упорядоченности дерева). Например, построенное раннее дерево после удаления узла 6 может стать таким, как показано на рис. 7.8.

 17
17


 7 18
7 18
5 
 9
9
8 12
Рис.7.8
Рассмотрим задачу обхода дерева. Существуют три способа обхода, которые естественно следуют из самой структуры дерева.
1) Обход слева направо: А,R,B (сначала посещаем левое поддерево, затем – корень и, наконец, правое дерево).
2) Обход сверху вниз: R, А, B (посещаем корень до поддеревьев).
3) Обход снизу вверх: А,B,R (посещаем корень после поддеревьев).
Интересно проследить результаты этих трех обходов на примере записи формул в виде дерева.
Например, формула
(a+b/c)*(d-e*f)
будет представлена так (рис. 7.9). 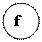




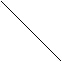














Рис. 7.9
(дерево формируется по принципу: операция – узел, операнды – поддеревья).
Обход 1 дает обычную инфиксную запись выражения (правда, без скобок).
Обход 2 – префиксную запись +a/bc-d*ef.
Обход 3 – постфиксную (ПОЛИЗ – польская инверсная запись): abc/+dcf*-*.
В качестве примера работы с древовидной структурой данных рассмотрим решение следующей задачи.
Вводятся фамилии абитуриентов; необходимо распечатать их в алфавитном порядке с указанием количества повторений каждой фамилии.
В программе будет использована рекурсивная функция der(), которая строит дерево фамилий, а также рекурсивная функция для печати дерева print_der(), в которой реализован первый способ обхода дерева.
#include<alloc.h>
#include<stdio.h>
#defint TREE struct der
TREE
{ char *w;
int c;
TREE *l;
TREE *r;
};
TREE *der (TREE *kr, char *word)
{
int sr;
if (kr==NULL)
{
kr=(TREE *)malloc (sizeof(TREE));
kr-->w=word; kr-->c=1;
kr-->1=kr-->r=NULL;
}
else if ((sr=strcmp(word, kr-->w))==0) kr-->c++;
else if (sr<0) kr-->1 = der(kr-->1, word);
else kr-->r = der(kr-->r, word);
return kr;
}
void print_der(TREE *kr)
{
if (kr)
{ print_der (kr->1);
printf(“слово - %-20s \t кол – во повтор. - %d\n”, kr->w, kr->c);
print_der (kr-->r);
}
}
void main ()
{ int i;
TREE *kr;
static char word [40] [21];
kr=NULL; i=0;
puts (“Введите <40 фамилий длиной <20 каждая”);
scanf(“%s”, word[i]);
while(word[i] [0]!=’\0’)
{ kr=der(kr,word[i]);
scanf (“%s”, word[++i]);
}
print_der(kr);
}
Рассмотрим еще один пример использования динамических структур данных. По введенной формуле необходимо построить ее ПОЛИЗ. (При записи формулы используются только операции +, -, *, / и буквы – операнды).
#include “stack.h” // в файле stack.h – описанные выше функции
#include <stdio.h> // работы со стеком
#include <stdlib.h>
#include <ctype.h>
#include <string.h>
#define ZNAK (c=’/ ‘)
void main()
{ char s[50], s1[80], c;
int er, i, l, k=0;
STACK *st=NULL;
puts(“Введите инфиксную запись формулы, операндами в которой”);
puts(“являются буквы, а знаками – символы +, -, *, /”);
gets(s);
l=strlen(s);
push(&st, ‘(‘); // заносим ‘(‘ в стек и
for(i=0; i<1; i++) // просматриваем выражение слева направо





 12
12





 45 45
45 45
 Потребность в организации стека возникает при решении, например, такой задачи. Пусть имеется текст, сбалансированный по круглым скобкам.
Потребность в организации стека возникает при решении, например, такой задачи. Пусть имеется текст, сбалансированный по круглым скобкам.



 …….
…….

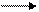



















 6
6
 5 9 23
5 9 23 7 12
7 12
 17
17

 18
18
 23
23


 17
17

 7 18
7 18
 9
9