Эти модели особенно эффективны для целей сертификации.
 Предполагается начать тестирование двумя независимыми группами.
Предполагается начать тестирование двумя независимыми группами.
N1, N2 – число обнаруженных каждой группой ошибок
N12 – число ошибок, обнаруженных дважды (обеими группами)
N – число ошибок в программе (неизвестное)
Е – эффективность тестирования

Предполагаем, что возможность обнаружения одинакова. Это серьезное предположение не лишенное смысла. Можно рассматривать каждое подмножество N как аппроксимацию всего пространства.
Если группа обнаружила некоторое количество ошибок, то она должна было найти примерно столько же ошибок всякого случайным образом выбранного подмножества, например: 

Статистическая модель Миллса
Сначала программа «засоряется» некоторым количеством известных ошибок. Эти ошибки вносятся в программу случайным образом, а затем делается предположение, что для ее собственных и внесенных ошибок вероятность обнаружения одинакова и зависит только от их количества.
N – первоначальное число ошибок в программе.
S – количество внесенных ошибок.
(n+V) – количество ошибок, обнаруженное при тестировании.
n – число собственных ошибок
 V – число внесенных ошибок
V – число внесенных ошибок
Оценка для N по методу максимального правдоподобия:
N можно оценивать после каждой ошибки. Миллс предлагает во время всего периода тестирования отмечать на графике число найденных ошибок и текущие оценки для N.
Вторая часть модели связана с выдвижением и проверкой гипотез о N.
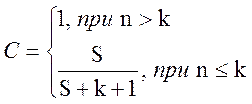 Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь
Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь  программа тестируется, пока не будут обнаружены все внесенные ошибки.
программа тестируется, пока не будут обнаружены все внесенные ошибки.
С – мера доверия к модели – вероятность того, что модель будет правильно
отклонять ложные предположения.
Имитационные модели
Модели имитируют процессы появления ошибок, процесс обнаружения ошибок, процесс исправления ошибок с точки зрения надежности ПО. Часто программу представляют как последовательность узлов, дуг и петель ориентированного графа.
Модель Шумана

Вводится ряд допущений и условий, основным из которых является условие существования программы исследователя системы. Остальные допущения и условия не связаны с какими-то специфическими свойствами ПО.
Условия сводятся к следующему:
1. Предполагается, что в начальный момент компоновки программных средств системы в них имеются небольшие ошибки (Е – количество ошибок). С этого времени отсчитывается время отладки  , которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени
, которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени  устанавливается
устанавливается  ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду остающихся в системе после времени
ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду остающихся в системе после времени  работы равно
работы равно
 I – общее число машинных команд.
I – общее число машинных команд.
2.  Предполагается, что значение функции частоты или интенсивности отказов
Предполагается, что значение функции частоты или интенсивности отказов  пропорциональна числу ошибок, оставшихся в ПО после израсходования на отладку времени
пропорциональна числу ошибок, оставшихся в ПО после израсходования на отладку времени  , то есть:
, то есть:
 C – коэффициент пропорциональности.
C – коэффициент пропорциональности.
Тогда, если время работы системы t отсчитывается от момента времени t0, а  остается фиксированным (
остается фиксированным ( =const), то функция надежности или вероятность безотказной работы на интервале времени от 0 до t есть
=const), то функция надежности или вероятность безотказной работы на интервале времени от 0 до t есть
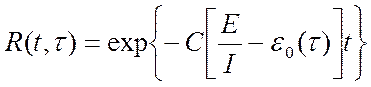
Для нахождения С и Е используются принцип максимального правдоподобия (пропорция).
Модель Джелинского-Моранды

Модель с дискретным убыванием интенсивности отказов. В этой модели предполагается, что интенсивность ошибок описывается кусочно-постоянной функцией, пропорциональной числу не устраненных ошибок. Т.е. предполагается, что интенсивность отказов  постоянна до обнаружения и исправления ошибки, после чего она опять становится постоянной, но с другим, меньшим, значением. При этом предполагается, что между
постоянна до обнаружения и исправления ошибки, после чего она опять становится постоянной, но с другим, меньшим, значением. При этом предполагается, что между  и числом оставшихся в программе ошибок существует прямая зависимость:
и числом оставшихся в программе ошибок существует прямая зависимость:

M – неизвестное первоначальное число ошибок
i – число обнаруженных ошибок, зависящих от времени t
 k – константа
k – константа
Частота обнаружения i -ой ошибки 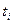 задается соотношением
задается соотношением
Значения неизвестных параметров k и M может быть оценено на основе последовательности наблюдений интервалов между моментами обнаружения ошибок по методу максимального правдоподобия.
Модель Миллса

Модель можно использовать для сертификации ПО. В модели не используются предположения о поведении функции риска  . Модель строится на твердом статистическом фундаменте.
. Модель строится на твердом статистическом фундаменте.
Сначала программа «засоряется» некоторым количеством известных ошибок. Эти ошибки вносятся в программу случайным образом, а затем делается предположение, что для ее собственных и внесенных ошибок вероятность обнаружения одинакова и зависит только от их количества.
N – первоначальное число ошибок в программе.
S – количество внесенных ошибок.
(n+V) – количество ошибок, обнаруженное при тестировании.
n – число собственных ошибок
 V – число внесенных ошибок
V – число внесенных ошибок
Оценка для N по методу максимального правдоподобия:
N можно оценивать после каждой ошибки. Миллс предлагает во время всего периода тестирования отмечать на графике число найденных ошибок и текущие оценки для N.
Вторая часть модели связана с выдвижением и проверкой гипотез о N.
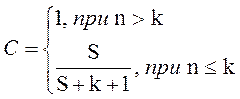 Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь
Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь  программа тестируется, пока не будут обнаружены все внесенные ошибки.
программа тестируется, пока не будут обнаружены все внесенные ошибки.
С – мера доверия к модели – вероятность того, что модель будет правильно
отклонять ложные предположения.
Минусы модели
С нельзя предсказать до тех пор, пока не будут обнаружены все внесенные ошибки, это может не произойти до самого конца этапа тестирования.
Модификация формулы для С, если не все ошибки обнаружены:
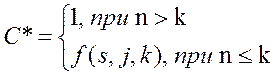 j – найденные внесенные ошибки, j < S
j – найденные внесенные ошибки, j < S
Модель математически проста и интуитивно привлекательна. Легко представить программу внесения ошибок, которая случайным образом выбирает модуль и вносит логические ошибки, изменяя или убирая операторы. Природа внесения ошибок должна оставаться в тайне, но все их следует регистрировать с целью последующего деления на собственные и несобственные.
Процесс внесения ошибок является самым слабым местом модели, поскольку предполагается, что для собственных и внесенных ошибок вероятность обнаружения одинакова, но неизвестна. Отсюда следует, что внесенные ошибки должны быть типичными, но на сегодня непонятно какими именно они должны быть. Однако по сравнению с проблемами других моделей эта проблема кажется не очень сложной и разрешимой.



 Предполагается начать тестирование двумя независимыми группами.
Предполагается начать тестирование двумя независимыми группами.


 V – число внесенных ошибок
V – число внесенных ошибок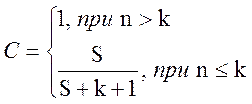 Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь
Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь  программа тестируется, пока не будут обнаружены все внесенные ошибки.
программа тестируется, пока не будут обнаружены все внесенные ошибки.
 , которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени
, которое включает затраты времени на выявление ошибок с помощью тестов, на контрольные проверки и т.д. При этом время исправного функционирования системы не учитывается. В течение времени  ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду остающихся в системе после времени
ошибок в расчете на одну команду машинного языка. Т.о. удельное число ошибок на одну машинную команду остающихся в системе после времени  I – общее число машинных команд.
I – общее число машинных команд. Предполагается, что значение функции частоты или интенсивности отказов
Предполагается, что значение функции частоты или интенсивности отказов  пропорциональна числу ошибок, оставшихся в ПО после израсходования на отладку времени
пропорциональна числу ошибок, оставшихся в ПО после израсходования на отладку времени  C – коэффициент пропорциональности.
C – коэффициент пропорциональности.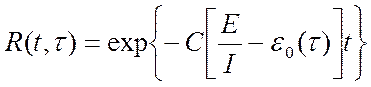
 постоянна до обнаружения и исправления ошибки, после чего она опять становится постоянной, но с другим, меньшим, значением. При этом предполагается, что между
постоянна до обнаружения и исправления ошибки, после чего она опять становится постоянной, но с другим, меньшим, значением. При этом предполагается, что между 
 k – константа
k – константа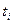 задается соотношением
задается соотношением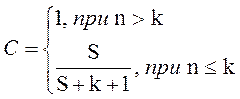 Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь
Примем, что программе имеется не более k собственных ошибок и внесем в нее еще S ошибок. Теперь 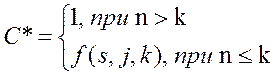 j – найденные внесенные ошибки, j < S
j – найденные внесенные ошибки, j < S


