Транспортир - это прибор, употребляемый для измерения углов, представляет собой полукруг, дуга которого разделена на 180 градусов.

Билет №9

Числовые промежутки

 

Отметим на координатной прямой точки с координатами -3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше -3 и меньше 2. Верно и обратное: если число х удовлетворяет условию -3<x<2, то оно изображается точкой, лежащей между точками с координатами -3 и 2.

Множество всех чисел, удовлетворяющих условию -3<x<2, называется числовым промежутком или просто промежутком от -3 до 2 и обозначается так: (-3;2).

На рисунках изображены множество чисел х, для которых выполняется неравенство х<10 и х≤10. Эти множества представляют собой промежутки, обозначаемые соответственно (-∞; 10) и (-∞; 10]. Читается так: число х принадлежит промежутку от минус бесконечности (-∞) до 10 (х<10) и число х принадлежит промежутку от минус бесконечности (-∞) до 10, включая число 10 (х≤10). Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В. Промежуток [3;5] является пересечением промежутков [-1;5] и [3;7]. Это можно записать так: [-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.

Объединение числовых промежутков

Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим.

Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают AB.

Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так:

Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество не является промежутком.

1. Числовым промежутком называется множество всех чисел, удовлетворяющих неравенству.

2. Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

3. Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В.

4. Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают.

1. Масштаб

Отношение длины отрезка на карте к длине соответствующего

отрезка на местности называют масштабом карты.

Масштаб 1: 20 000 000 значит, что в 1см карты умещается 200км

местности, или в одном сантиметре карты 1км местности.

Билет №10

1. Прямоугольная система координат

1. Осевая симметрия

«Симметрия» - слово греческого происхождения. Оно означает соразмерность, наличие определенного порядка, закономерности в расположении частей.

Люди с давних времен использовали симметрию в рисунках, орнаментах, предметах быта.
Симметрия широко распространена в природе. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, мозаике в храме, морской звезде.
Симметрия широко используется на практике, в строительстве и технике. Это строгая симметрия в форме античных зданий, гармоничные древнегреческие вазы, здании Кремля, машинах, самолетах и многом другом. Примерами использования симметрии являются паркет и бордюр.

 

Билет № 11

1. Вычитание рациональных чисел

Число, которое можно записать в виде отношения а / n, где а —

целое число, a n — натуральное число,

называют рациональным числом.

Например:

Любое целое число а является рациональным числом,

так как его можно записать в виде a / 1.

 

Сумма, разность и произведение рациональных чисел тоже

рациональные числа.

Можно ли от меньшего числа вычесть большее? Так, если действуем с рациональными числами. Во время вычитания рациональных чисел уменьшающееся может быть меньше, чем вычитаемое.

Правила вычитания рациональных чисел.

Запомните!

Правило замены вычитания сложением Чтобы от одного числа вычесть другое, можно до уменьшаемого прибавить число, противоположное вычитателя:

а - b = а + (-b).

:Обратите внимание:

1) в результате вычитания рациональных чисел уменьшающееся:

— уменьшается, если вычитаемое является положительным;

— увеличивается. если вычитаемое является отрицательным;

— не меняется, если вычитаемое равно 0;

2) о вычитания рационального числа а от числа b говорят: число b изменили на число a.

1. Окружность. Длина окружности

Окруж­ность – мно­же­ство всех точек на плос­ко­сти, рав­но­уда­лен­ных от дан­ной точки.

Т. е. есть неко­то­рая точка, мы за­да­ем ка­кое-то рас­сто­я­ние – ра­ди­ус окруж­но­сти – и берем все точки, ко­то­рые на­хо­дят­ся от ис­ход­ной на дан­ном рас­сто­я­нии

Так как от­но­ше­ние длины окруж­но­сти к ра­ди­у­су – по­сто­ян­ное число, то и от­но­ше­ние длины к диа­мет­ру – по­сто­ян­ное число.

Итак, пусть длина окруж­но­сти , а диа­метр окруж­но­сти – . Так как от­но­ше­ние длины к диа­мет­ру все­гда по­сто­ян­ное, то его можно при­мер­но по­счи­тать. Про­де­лав это, вы при­мер­но по­лу­чи­те число Так как число, ко­то­рое равно от­но­ше­нию длины окруж­но­сти к ее диа­мет­ру, не могли по­счи­тать точно, его обо­зна­чи­ли спе­ци­аль­ной бук­вой, бук­вой (буква гре­че­ско­го ал­фа­ви­та).

 

Билет №12

1. Степень числа

Общеизвестный факт что сумму нескольких равных слагаемых можно найти с помощью умножения. Например: 5+5+5+5+5+5=5х6. О таком выражении говорят, что сумму равных слагаемых свернули в произведение. И наоборот, если читать это равенство справа налево, получаем, что мы развернули сумму равных слагаемых. Аналогично можно сворачивать произведение нескольких равных множителей 5х5х5х5х5х5=5⁶.

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5⁶ и говорят «пять в шестой степени».

Выражение 5⁶- это степенью числа, где:

5 - основание степени;

6 - показатель степени.

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а

1. Смежные углы

Смежными угламиназывается пара углов с общей вершиной и одной общей стороной. 2 оставшиеся стороны делают продолжение друг другу, образовывая прямую линию. Для угла 135 градусов смежным будет угол равный 45 градусам. Для угла x градусов смежным является угол (180 – x) градусов.

 

 

Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.   При пересечении 2-х прямых получается 4-ре пары смежных углов:

Смежные углы равны: сумма смежных углов 180º.

 

• Если 2 угла равны, то смежные им углы тоже равны.

• Если угол не развернутый, значит он ≠180°.

• Смежный угол для прямого угла (т.е. угла, у него градусная мера = 90°), тоже прямой.

• Смежный угол для острого угла (градусная мера меньше 90°), будет тупым (градусная мера больше

90°), а смежный тупому - острым.

 

 

 

Билет №13

1. Среднее арифметическое

Среднее арифметическое нескольких чисел равно сумме этих чисел, деленной на количество слагаемых в этой сумме. Например: среднее арифметическое a и b равно x = (a + b): 2; среднее арифметическое a, b и c равно x = (a + b + c): 3; среднее арифметическое a, b, c и d равно x = a+b+c+d   и т. д.

Координата точки C(6) является средним арифметическим координат точек A(3) и B(9). 6 = 3+9   . Обратите внимание на равенство отрезков AC и CB. Точка С делит отрезок АВ пополам.

Угол. Развернутый угол

Развернутый угол - это угол, стороны которого составляют прямую (рис. 1).

Градусная мера развернутого угла равна .

Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют одну общую сторону, а две другие составляют прямую. Такие углы называются смежными.

Биссектриса развернутого угла делит его на два прямых угла.

Если произвольный луч, проведенный из вершины развернутого угла, не является биссектрисой, то он делит развернутый угол на два, один из которых острый (меньше прямого), а другой - тупой (больше прямого)

Билет №14

 

Рациональные числа

Число, которое можно записать в виде отношения а / n, где а —

целое число, a n — натуральное число,

называют рациональным числом.

Рациональные числа — это числа, которые могут быть представлены в виде дроби , где a — это числитель дроби, b — знаменатель дроби. При чем b не должно быть нулём, поскольку деление на ноль не допускается.

К рациональным числам относятся следующие категории чисел:

· целые числа (например −2, −1, 0 1, 2 и т.д.)

· обыкновенные дроби (например , , и т.п.)

· смешанные числа (например , , и т.п.)

· десятичные дроби (например 0,2 и т.п.)

· бесконечные периодические дроби (например 0,(3) и т.п.)

Каждое число из этой категории может быть представлено в виде дроби .

Измерение углов

Измерение углов сводится к измерению соответствующих им дуг следующим образом. За единицу углов принимают угол, составляющий 1/90 часть прямого угла. Эту единицу называют угловым градусом.

За единицу дуг одинакового радиуса принимают такую дугу того же радиуса, которая соответствуетцентральному углу

, равному угловому градусу. Такая дуга называется дуговым градусом.

Так как прямому центральному углу соответствует 1/4 окружности, то угловому градусу соответствует 1/90 четверти окружности. Значит, дуговой градус составляет 1/360 целой окружности.

Билет №15

1. Умножение и деление обыкновенных дробей

Распечатать

Билет №16

 

1. Деление десятичной дроби на десятичную дробь\

Чтобы разделить одну десятичную дробь на другую, переносим запятую вправо и в делимом, и в делителе на столько знаков, сколько их в делителе после запятой, то есть на три знака. Таким образом, 0,1218: 0,058 = 121,8: 58. Деление на десятичную дробь заменили делением на натуральное число. Делим уголком. Имеем: 0,1218: 0,058 = 121,8: 58 = 2,1.

 

 

 

1. Треугольник

Билет №17

1, Простые числа. Разложение числа на простые множители

Про­стым на­зы­ва­ют число, ко­то­рое имеет ровно два раз­лич­ных де­ли­те­ля.

Раз­ло­жить на­ту­раль­ное число на мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния на­ту­раль­ных чисел.

Раз­ло­жить на­ту­раль­ное число на про­стые мно­жи­те­ли – зна­чит пред­ста­вить его в виде про­из­ве­де­ния про­стых чисел.

Всякое составное число можно разложить на простые множители.

При любом способе получается одно и то же разложение,

если не учитывать порядка записи множителей.

Последовательность действий при разложении на простые множители:

1. Проверяем, не является ли предложенное число простым.

2. Если нет, то подбираем, руководствуясь признаками деления

делитель,

из простых чисел начиная с наименьшего (2, 3, 5 …).

3. Повторяем это действие до тех пор, пока частное не окажется

простым числом.

Разложим на простые множители число 27:

 

 

27 не является простым.

27 на 2 не делится.

27 делится на 3, получаем 27: 3 = 9.

9 на 2 не делится.

9 делится на 3, 9: 3 = 3.

3 простое число.

Результат: 27 = 3 • 3 • 3.

 

27 3

9 3

3 3

 

Разложим на простые множители число 378:

 

378 2

189 3

63 3

21 3

7 7

 

378 не является простым.

378 делится на 2,

так как оканчивается на четное число (8).

378: 2 = 189.

189 делится на 3,

потому что сумма его цифр делится на 3,

получаем 189: 3 = 63.

63 так же делится на 3, получаем 63: 3 = 21.

21 так же делится на 3, получаем 21: 3 =7

7 простое число.

Вертикальные углы

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

∠1 и ∠2 — вертикальные углы

При пересечении двух прямых образуется две пары вертикальных углов:

 

∠3 и ∠4 — вертикальные углы

 

Билет №18

1. Наибольший делитель.

Наибольший общий делитель (НОД) двух и более чисел — это
самое большее натуральное число, на которое эти числа делятся
без остатка.

Например:

у чисел 12 и 8 наибольший общий делитель (НОД) равен 4,

а у чисел 20 и 35 (НОД) равен 5

 

Если у нескольких чисел нет общих делителей кроме единицы, то эти
числа называются взаимно простыми.

Например:

у чисел 5 и 8, 11 и 18, 16 и 27 (НОД) равен 1.

Для нахождения наибольшего общего делителя двух или более чисел,
например 36 и 24, надо:

1) разложить их на простые множители;

36 = 2 • 2 • 3 • 3; 24 = 2 • 2 • 2 • 3.

2) в группах множителей (2 • 2 • 3 • 3) и (2 • 2 • 2 • 3), входящих в
разложение этих чисел, оставляем только совпадающие множители;

(2 • 2 • 3) и (2 • 2 • 3)

3) найти произведение оставшихся множителей. 2 • 2 • 3 = 12

Наибольший общий делитель чисел 36 и 24 равен 12.

 

Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.

Например: у чисел 12, 36 и 48 НОД = 12.

1. Площадь треугольника

 

Чтобы найти площадь прямоугольного треугольника необходимо знать длину основания и высоту. В прямоугольном треугольнике высоту заменяет одна из сторон. Поэтому в формулу площади треугольника вместо высоты подставляем одну из сторон.

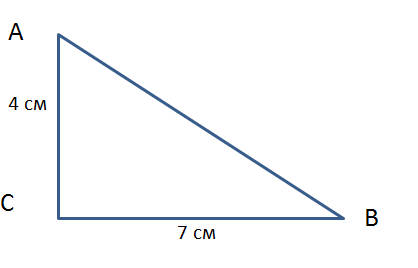
В нашем примере стороны равны 7 см и 4 см. Формула для расчета площади треугольника записывается так:
S _{прямоугольного треугольника АВС} = ВС * СА: 2

Подставим в формулу наши данные и получим:
S _{прямоугольного треугольника АВС} = 7 см * 4 см: 2 = 14 см²

Теперь рассмотрим произвольный треугольник.

Для такого треугольника необходимо провести высоту к основанию.
В нашем примере высота равна 6 см, а основание равно 8 см. Как и в предыдущем примере, рассчитываем площадь по формуле:
S _{произвольного треугольника АВС} = ВС * h: 2.

Подставим в формулу наши данные и получим:
S _{произвольного треугольника АВС} = 8 см * 6 см: 2 = 24 см².

 

 

Билет №19

1. Наименьшее общее кратное

Наименьшим общим кратным натуральных чисел a и b называют
наименьшее натуральное число, которое кратно и a, и b.

Чтобы найти наименьшее общее кратное нескольких натуральных
чисел, например 6 и 8, надо:

1) разложить их на простые множители;

6 = 2 • 3;

8 = • 2 • 2;

2 есть в разложении числа 6 (вычеркиваем ее);

2) выписать множители, входящие в разложение одного из чисел;

2 • 3;

3) домножить их на недостающие множители из разложений
остальных чисел;

2 • 3 • 2 • 2;

4) найти произведение получившихся множителей.

2 • 3 • 2 • 2 = 24;

НОК (6 и 8) = 24.

Найдем наименьшее общее кратное чисел 24 и 36:

1) разложим их на простые множители;

24 = 2 • 2 • 2 • 3;

36 = • 3;

2, 2 и 3 есть в разложении числа 24 (вычеркиваем их);

2) выпишем множители, входящие в разложение числа 24;

2 • 2 • 2 • 3;

3) домножим их на недостающий множитель из разложения числа 36;

2 • 2 • 2 • 3 • 3;

4) найти произведение получившихся множителей.

2 • 2 • 2 • 3 • 3 = 72;

НОК (24 и 36) = 72.

Найдем наименьшее общее кратное чисел 30 и 42: 1) разложим их на простые множители; 30 = 2 • 3 • 5; 42 = • 7; 2 и 3 есть в разложении числа 30 (вычеркиваем их); 2) выпишем множители, входящие в разложение числа 30; 2 • 3 • 5; 3) домножим их на недостающий множитель из разложения числа 42; 2 • 3 • 5 • 7; 4) найти произведение получившихся множителей. 2 • 3 • 5 • 7 = 210; НОК (30 и 42) = 210.

Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел. Например: у чисел 12, 6 и 4 НОК = 12.

 

1. Диаграммы

 

Диаграммы являются графическим изображением данных (цифры, факты и пр.) с целью их наглядного представления. Диаграмма – чертеж, на котором статистические данные изображаются с помощью геометрических фигур или рисунков.

 

Основная задача при работе с диаграммой – сопоставление, сравнение числовых величин, выработка умения объяснить полученные соотношения, делать выводы. Выбор типа диаграммы зависит от тех задач, для решения которых она предназначена. Диаграмма должна быть достаточно простой и наглядной.

 

 

Билет №20

1. Признаки делимости натуральных чисел

Для упрощения деления натуральных чисел были выведены правила деления на числа первого десятка и числа 11, 25, которые объединены в раздел признаков делимости натуральных чисел.

Натуральные числа, имеющие в первом разряде цифры (оканчивающиеся на) 2,4,6,8,0, называются четными.

 

На 2 делятся все четные натуральные числа, например: 172, 94,67 838, 1670.

 

На 3 делятся все натуральные числа, сумма цифр которых кратна 3. Например:
39 (3 + 9 = 12; 12: 3 = 4);

16 734 (1 + 6 + 7 + 3 + 4 = 21; 21:3 = 7).

На 4 делятся все натуральные числа, две последние цифры которых составляют нули или число, кратное 4. Например:
124 (24: 4 = 6);
103 456 (56: 4 = 14).

 

На 5 делятся все натуральные числа, оканчивающиеся на 5 или 0. Например: 125; 10 720.

 

На 6 делятся те натуральные числа, которые делятся на 2 и на 3 одновременно (все четные числа, которые делятся на 3). Например: 126 (б — четное, 1 + 2 + 6 = 9, 9: 3 = 3).

 

На 9 делятся те натуральные числа, сумма цифр которых кратна 9. Например:
1179 (1 + 1 + 7 + 9 = 18, 18: 9 = 2).

 

На 10 делятся все натуральные числа, оканчивающиеся на 0. Например: 30; 980; 1 200; 1 570.

 

На 11 делятся только те натуральные числа, у которых сумма цифр, занимающих четные места, равна сумме цифр, занимающих нечетные места, или разность суммы цифр нечетных мест и суммы цифр четных мест кратна 11. Например:
105787 (1 + 5 + 8 = 14 и 0 + 7 + 7 = 14);
9 163 627 (9 + 6 + б + 7 = 28 и 1 + 3 + 2 = 6);
28 — 6 = 22; 22: 11 = 2).

 

На 25 делятся те натуральные числа, две последние цифры которых — нули или составляют число, кратное 25. Например:
2 300; 650 (50: 25 = 2);

1 475 (75: 25 = 3).

На разрядную единицу делятся те натуральные числа, у которых количество нулей больше или равно количеству нулей разрядной единицы. Например: 12 000 делится на 10, 100 и 1000.

 

1. Свойства углов треугольника

Треугольник — фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.
Точки называют вершинами треугольника, а отрезки — сторонами треугольника.

 

Сумма углов треугольника равна 180​∘​​.

У любого треугольника хотя бы два угла острые.

Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

 

Билет №9

Числовые промежутки

 

Отметим на координатной прямой точки с координатами -3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше -3 и меньше 2. Верно и обратное: если число х удовлетворяет условию -3<x<2, то оно изображается точкой, лежащей между точками с координатами -3 и 2.

Множество всех чисел, удовлетворяющих условию -3<x<2, называется числовым промежутком или просто промежутком от -3 до 2 и обозначается так: (-3;2).

На рисунках изображены множество чисел х, для которых выполняется неравенство х<10 и х≤10. Эти множества представляют собой промежутки, обозначаемые соответственно (-∞; 10) и (-∞; 10]. Читается так: число х принадлежит промежутку от минус бесконечности (-∞) до 10 (х<10) и число х принадлежит промежутку от минус бесконечности (-∞) до 10, включая число 10 (х≤10). Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В. Промежуток [3;5] является пересечением промежутков [-1;5] и [3;7]. Это можно записать так: [-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.

Объединение числовых промежутков

Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим.

Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают AB.

Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так:

Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество не является промежутком.

1. Числовым промежутком называется множество всех чисел, удовлетворяющих неравенству.

2. Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.

3. Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В.

4. Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают.

1. Масштаб

Отношение длины отрезка на карте к длине соответствующего

отрезка на местности называют масштабом карты.

Масштаб 1: 20 000 000 значит, что в 1см карты умещается 200км

местности, или в одном сантиметре карты 1км местности.

Билет №10

1. Прямоугольная система координат

1. Осевая симметрия

«Симметрия» - слово греческого происхождения. Оно означает соразмерность, наличие определенного порядка, закономерности в расположении частей.

Люди с давних времен использовали симметрию в рисунках, орнаментах, предметах быта.
Симметрия широко распространена в природе. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, мозаике в храме, морской звезде.
Симметрия широко используется на практике, в строительстве и технике. Это строгая симметрия в форме античных зданий, гармоничные древнегреческие вазы, здании Кремля, машинах, самолетах и многом другом. Примерами использования симметрии являются паркет и бордюр.

 

Билет № 11

1. Вычитание рациональных чисел

Число, которое можно записать в виде отношения а / n, где а —

целое число, a n — натуральное число,

называют рациональным числом.

Например:

Любое целое число а является рациональным числом,

так как его можно записать в виде a / 1.

 

Сумма, разность и произведение рациональных чисел тоже

рациональные числа.

Можно ли от меньшего числа вычесть большее? Так, если действуем с рациональными числами. Во время вычитания рациональных чисел уменьшающееся может быть меньше, чем вычитаемое.

Правила вычитания рациональных чисел.

Запомните!

Правило замены вычитания сложением Чтобы от одного числа вычесть другое, можно до уменьшаемого прибавить число, противоположное вычитателя:

а - b = а + (-b).

:Обратите внимание:

1) в результате вычитания рациональных чисел уменьшающееся:

— уменьшается, если вычитаемое является положительным;

— увеличивается. если вычитаемое является отрицательным;

— не меняется, если вычитаемое равно 0;

2) о вычитания рационального числа а от числа b говорят: число b изменили на число a.

1. Окружность. Длина окружности

Окруж­ность – мно­же­ство всех точек на плос­ко­сти, рав­но­уда­лен­ных от дан­ной точки.

Т. е. есть неко­то­рая точка, мы за­да­ем ка­кое-то рас­сто­я­ние – ра­ди­ус окруж­но­сти – и берем все точки, ко­то­рые на­хо­дят­ся от ис­ход­ной на дан­ном рас­сто­я­нии

Так как от­но­ше­ние длины окруж­но­сти к ра­ди­у­су – по­сто­ян­ное число, то и от­но­ше­ние длины к диа­мет­ру – по­сто­ян­ное число.

Итак, пусть длина окруж­но­сти , а диа­метр окруж­но­сти – . Так как от­но­ше­ние длины к диа­мет­ру все­гда по­сто­ян­ное, то его можно при­мер­но по­счи­тать. Про­де­лав это, вы при­мер­но по­лу­чи­те число Так как число, ко­то­рое равно от­но­ше­нию длины окруж­но­сти к ее диа­мет­ру, не могли по­счи­тать точно, его обо­зна­чи­ли спе­ци­аль­ной бук­вой, бук­вой (буква гре­че­ско­го ал­фа­ви­та).

 

Билет №12

1. Степень числа

Общеизвестный факт что сумму нескольких равных слагаемых можно найти с помощью умножения. Например: 5+5+5+5+5+5=5х6. О таком выражении говорят, что сумму равных слагаемых свернули в произведение. И наоборот, если читать это равенство справа налево, получаем, что мы развернули сумму равных слагаемых. Аналогично можно сворачивать произведение нескольких равных множителей 5х5х5х5х5х5=5⁶.

То есть вместо умножения шести одинаковых множителей 5х5х5х5х5х5 пишут 5⁶ и говорят «пять в шестой степени».

Выражение 5⁶- это степенью числа, где:

5 - основание степени;

6 - показатель степени.

Действия, с помощью которых произведение равных множителей сворачивают в степень, называют возведением в степень.

Возвести число a в степень n – значит найти произведение n множителей, каждый из которых равен а

1. Смежные углы

Смежными угламиназывается пара углов с общей вершиной и одной общей стороной. 2 оставшиеся стороны делают продолжение друг другу, образовывая прямую линию. Для угла 135 градусов смежным будет угол равный 45 градусам. Для угла x градусов смежным является угол (180 – x) градусов.

 

 

Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.   При пересечении 2-х прямых получается 4-ре пары смежных углов:

Смежные углы равны: сумма смежных углов 180º.

 

• Если 2 угла равны, то смежные им углы тоже равны.

• Если угол не развернутый, значит он ≠180°.

• Смежный угол для прямого угла (т.е. угла, у него градусная мера = 90°), тоже прямой.

• Смежный угол для острого угла (градусная мера меньше 90°), будет тупым (градусная мера больше

90°), а смежный тупому - острым.

 

 

 

Билет №13

1. Среднее арифметическое

Среднее арифметическое нескольких чисел равно сумме этих чисел, деленной на количество слагаемых в этой сумме. Например: среднее арифметическое a и b равно x = (a + b): 2; среднее арифметическое a, b и c равно x = (a + b + c): 3; среднее арифметическое a, b, c и d равно x = a+b+c+d   и т. д.

Координата точки C(6) является средним арифметическим координат точек A(3) и B(9). 6 = 3+9   . Обратите внимание на равенство отрезков AC и CB. Точка С делит отрезок АВ пополам.

Угол. Развернутый угол

Развернутый угол - это угол, стороны которого составляют прямую (рис. 1).

Градусная мера развернутого угла равна .

Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют одну общую сторону, а две другие составляют прямую. Такие углы называются смежными.

Биссектриса развернутого угла делит его на два прямых угла.

Если произвольный луч, проведенный из вершины развернутого угла, не является биссектрисой, то он делит развернутый угол на два, один из которых острый (меньше прямого), а другой - тупой (больше прямого)

Билет №14

 

Рациональные числа

Число, которое можно записать в виде отношения а / n, где а —

целое число, a n — натуральное число,

называют рациональным числом.

Рациональные числа — это числа, которые могут быть представлены в виде дроби , где a — это числитель дроби, b — знаменатель дроби. При чем b не должно быть нулём, поскольку деление на ноль не допускается.

К рациональным числам относятся следующие категории чисел:

· целые числа (например −2, −1, 0 1, 2 и т.д.)

· обыкновенные дроби (например , , и т.п.)

· смешанные числа (например , , и т.п.)

· десятичные дроби (например 0,2 и т.п.)

· бесконечные периодические дроби (например 0,(3) и т.п.)

Каждое число из этой категории может быть представлено в виде дроби .

Измерение углов

Измерение углов сводится к измерению соответствующих им дуг следующим образом. За единицу углов принимают угол, составляющий 1/90 часть прямого угла. Эту единицу называют угловым градусом.

За единицу дуг одинакового радиуса принимают такую дугу того же радиуса, которая соответствуетцентральному углу

, равному угловому градусу. Такая дуга называется дуговым градусом.

Так как прямому центральному углу соответствует 1/4 окружности, то угловому градусу соответствует 1/90 четверти окружности. Значит, дуговой градус составляет 1/360 целой окружности.

Транспортир - это прибор, употребляемый для измерения углов, представляет собой полукруг, дуга которого разделена на 180 градусов.

 

Чтобы измерить угол AOB, накладывают на него прибор так, чтобы центр полукруга совпал с вершиной угла, а радиусом OM совпал со стороной AO. Тогда число градусов, содержащееся в дуге PN, покажет величину угла AOB. При помощи транспортира можно также начертить угол, содержащий данное число градусов.

 

Так как прямой угол содержит 90°, то:

1. сумма углов всякого треугольника равна 180 °;

2. сумма острых углов прямоугольного треугольника равна 90°;

3. каждый угол равностороннего треугольника равен 60°;

4. сумма углов выпуклого многоугольника, имеющего n сторон, равна 180° (n - 2).

 

 

Билет №15

1. Умножение и деление обыкновенных дробей

Распечатать