Если существует решение задачи (26), то, согласно доверительному методу [2], эта задача эквивалентна следующей минимаксной задаче:
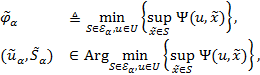 (29)
(29)
где  есть семейство всех доверительных множеств
есть семейство всех доверительных множеств  уровня
уровня 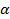 , т.е. таких, что
, т.е. таких, что 
 . Эквивалентность здесь понимается в следующем смысле:
. Эквивалентность здесь понимается в следующем смысле:
1) 
2) для каждой стратегии  , оптимальной в задаче (26), найдется доверительное множество
, оптимальной в задаче (26), найдется доверительное множество  такое, что пара
такое, что пара 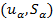 является оптимальной в задаче (29);
является оптимальной в задаче (29);
3) для каждой пары  , оптимальной в задаче (29), стратегия
, оптимальной в задаче (29), стратегия  является оптимальной и в задаче (26).
является оптимальной и в задаче (26).
Задача (29) может быть записана в следующей эквивалентной форме
 (30)
(30)
при ограничениях

Вследствие эквивалентности задач (29) и (30), оптимальное решение задачи (30) есть  .
.
Предположим, что случайный вектор  , а значит и случайный вектор
, а значит и случайный вектор  , имеет дискретное распределение с конечным числом реализаций. Пусть
, имеет дискретное распределение с конечным числом реализаций. Пусть  ,
,  , — возможные реализации случайного вектора
, — возможные реализации случайного вектора  , а
, а  ,
,  , — возможные реализации случайного вектора
, — возможные реализации случайного вектора  . Заданы вероятности каждой реализации
. Заданы вероятности каждой реализации  ,
,  .
.
В случае, когда вектор  имеет дискретное распределение, оптимальное доверительное множество состоит из тех реализаций случайного вектора
имеет дискретное распределение, оптимальное доверительное множество состоит из тех реализаций случайного вектора  , суммарная вероятность которых не менее
, суммарная вероятность которых не менее 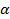 . Таким образом, можно заменить оптимизацию по доверительным множествам на оптимизацию по всем, имеющим вероятностную меру не менее
. Таким образом, можно заменить оптимизацию по доверительным множествам на оптимизацию по всем, имеющим вероятностную меру не менее 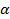 , подмножествам множества
, подмножествам множества  . Введём вектор
. Введём вектор  c координатами
c координатами 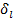 ,
,  , по правилу
, по правилу

где  . Итак, каждому возможному значению вектора
. Итак, каждому возможному значению вектора  соответствует некоторое подмножество
соответствует некоторое подмножество  множества
множества 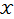 и наоборот.
и наоборот.
Пусть известна величина  , являющаяся оценкой снизу величин
, являющаяся оценкой снизу величин  ,
,  ,
,  , т.е.
, т.е.

Рассмотрим следующую задачу:
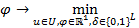 (32)
(32)
при ограничениях
 ,
,  ; (33)
; (33)

Пусть  — оптимальное решение задачи (32).
— оптимальное решение задачи (32).
Справедлива следующая теорема.
Теорема 2. Пусть 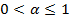 ,
,  ,
,  ,
,  ,
,  и выполнено условие (28). Тогда решения задач (29) и (32) существуют и данные задачи эквиваленты в следующем смысле:
и выполнено условие (28). Тогда решения задач (29) и (32) существуют и данные задачи эквиваленты в следующем смысле:
1) оптимальное значение критерия  в задаче (29) равно
в задаче (29) равно  ;
;
2)  является оптимальной стратегией в задаче (29);
является оптимальной стратегией в задаче (29);
3) одно из оптимальных доверительных множеств в (29) имеет вид:
 (35)
(35)
Доказательство. Рассмотрим случай  . Условия
. Условия  ,
,  ,
,  ,
,  и (28) обеспечивают существование решения задачи согласно следствию к теореме 1. Покажем, что
и (28) обеспечивают существование решения задачи согласно следствию к теореме 1. Покажем, что 
 . В силу ограничений задачи (30)
. В силу ограничений задачи (30)

Как было отмечено выше, оптимальное доверительное множество 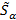 содержится в множестве
содержится в множестве 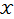 , т. е. состоит из конечного числа реализаций случайного вектора
, т. е. состоит из конечного числа реализаций случайного вектора  . Пусть вектор
. Пусть вектор  составлен по следующему правилу:
составлен по следующему правилу:  , если
, если 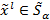 ;
;  в противном случае. Заметим, что ограничения задачи (32), которая эквивалентна задаче (29), будут выполнены для тройки
в противном случае. Заметим, что ограничения задачи (32), которая эквивалентна задаче (29), будут выполнены для тройки  . Те ограничения, которые соответствуют единичным координатам вектора
. Те ограничения, которые соответствуют единичным координатам вектора  , выполнены согласно (36). А ограничения, в которые входят нулевые координаты вектора
, выполнены согласно (36). А ограничения, в которые входят нулевые координаты вектора  , по определению числа
, по определению числа  являются пассивными в том случае, если хотя бы одна координата вектора
являются пассивными в том случае, если хотя бы одна координата вектора  равна единице, что равносильно требованию
равна единице, что равносильно требованию  . Доказано, что
. Доказано, что 
 .
.
Теперь докажем обратное неравенство 
 . Условие
. Условие  обеспечивает, что хотя бы одна из координат вектора
обеспечивает, что хотя бы одна из координат вектора  равна единице. Поэтому ограничения (33), которые содержат нулевые координаты вектора
равна единице. Поэтому ограничения (33), которые содержат нулевые координаты вектора  , являются пассивными, значит их можно исключить из системы ограничений. Следовательно, выполнение ограничений задачи (32) обеспечивает выполнение ограничений задачи (30) для тройки
, являются пассивными, значит их можно исключить из системы ограничений. Следовательно, выполнение ограничений задачи (32) обеспечивает выполнение ограничений задачи (30) для тройки  .
.
Таким образом, доказано, что  . При этом стратегия
. При этом стратегия  и множество
и множество  являются обеспечивающими оптимальное значение критерия в задаче (7), что доказывает второй и третий пункт утверждения.
являются обеспечивающими оптимальное значение критерия в задаче (7), что доказывает второй и третий пункт утверждения.
Рассмотрим случай  . Тогда в задаче (32)
. Тогда в задаче (32)  , а в задаче (29)
, а в задаче (29)  . При подстановке найденных оптимальных значений
. При подстановке найденных оптимальных значений  ,
, 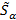 в ограничения соответствующих задач, получаются задачи с одинаковыми ограничениями, а значит, их решения совпадают. При этом в силу условий следствия к теореме 1 множество
в ограничения соответствующих задач, получаются задачи с одинаковыми ограничениями, а значит, их решения совпадают. При этом в силу условий следствия к теореме 1 множество  непусто и множество
непусто и множество  состоит только из нулевого вектора, значит решение задачи существует и при
состоит только из нулевого вектора, значит решение задачи существует и при  . Итак, утверждение теоремы доказано.■
. Итак, утверждение теоремы доказано.■
Заметим, что задача (32) содержит большое число пассивных ограничений. Рассмотрим ограничения  при фикcированном
при фикcированном 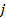 . Пусть
. Пусть  — квантиль уровня
— квантиль уровня 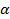 распределения случайной величины
распределения случайной величины 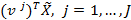 . В силу условия (34), ограничения, соответствующие величинам
. В силу условия (34), ограничения, соответствующие величинам  , удовлетворяющим условию
, удовлетворяющим условию  , являются пассивными. Поэтому их можно исключить из системы ограничений задачи (32), тем самым значительно понизив размерность решаемой задачи.
, являются пассивными. Поэтому их можно исключить из системы ограничений задачи (32), тем самым значительно понизив размерность решаемой задачи.
Задача (32) по сути является детерминированным эквивалентом исходной задачи в виде смешанной задачи линейного программирования. Для её решения можно применять специальные методы линейного программирования, например метод Бендерса[13]. Также для решения данных задач существуют эффективные программные средства, среди которых LPSolve [14].



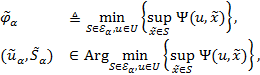 (29)
(29) есть семейство всех доверительных множеств
есть семейство всех доверительных множеств  уровня
уровня 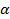 , т.е. таких, что
, т.е. таких, что 
 . Эквивалентность здесь понимается в следующем смысле:
. Эквивалентность здесь понимается в следующем смысле:
 , оптимальной в задаче (26), найдется доверительное множество
, оптимальной в задаче (26), найдется доверительное множество  такое, что пара
такое, что пара 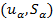 является оптимальной в задаче (29);
является оптимальной в задаче (29); , оптимальной в задаче (29), стратегия
, оптимальной в задаче (29), стратегия  является оптимальной и в задаче (26).
является оптимальной и в задаче (26). (30)
(30)
 .
. , а значит и случайный вектор
, а значит и случайный вектор  , имеет дискретное распределение с конечным числом реализаций. Пусть
, имеет дискретное распределение с конечным числом реализаций. Пусть  ,
,  , — возможные реализации случайного вектора
, — возможные реализации случайного вектора  ,
,  ,
,  .
. . Введём вектор
. Введём вектор  c координатами
c координатами 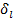 ,
, 
 . Итак, каждому возможному значению вектора
. Итак, каждому возможному значению вектора  соответствует некоторое подмножество
соответствует некоторое подмножество  множества
множества 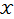 и наоборот.
и наоборот. , являющаяся оценкой снизу величин
, являющаяся оценкой снизу величин  ,
,  ,
, 
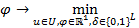 (32)
(32) ,
,  ; (33)
; (33)
 — оптимальное решение задачи (32).
— оптимальное решение задачи (32).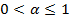 ,
,  ,
,  ,
,  ,
,  и выполнено условие (28). Тогда решения задач (29) и (32) существуют и данные задачи эквиваленты в следующем смысле:
и выполнено условие (28). Тогда решения задач (29) и (32) существуют и данные задачи эквиваленты в следующем смысле: в задаче (29) равно
в задаче (29) равно  ;
; является оптимальной стратегией в задаче (29);
является оптимальной стратегией в задаче (29); (35)
(35) . Условия
. Условия 

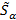 содержится в множестве
содержится в множестве  составлен по следующему правилу:
составлен по следующему правилу:  , если
, если 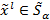 ;
;  в противном случае. Заметим, что ограничения задачи (32), которая эквивалентна задаче (29), будут выполнены для тройки
в противном случае. Заметим, что ограничения задачи (32), которая эквивалентна задаче (29), будут выполнены для тройки  . Те ограничения, которые соответствуют единичным координатам вектора
. Те ограничения, которые соответствуют единичным координатам вектора  . Доказано, что
. Доказано, что 
 равна единице. Поэтому ограничения (33), которые содержат нулевые координаты вектора
равна единице. Поэтому ограничения (33), которые содержат нулевые координаты вектора  .
. . При этом стратегия
. При этом стратегия  являются обеспечивающими оптимальное значение критерия в задаче (7), что доказывает второй и третий пункт утверждения.
являются обеспечивающими оптимальное значение критерия в задаче (7), что доказывает второй и третий пункт утверждения. . Тогда в задаче (32)
. Тогда в задаче (32)  , а в задаче (29)
, а в задаче (29)  . При подстановке найденных оптимальных значений
. При подстановке найденных оптимальных значений  непусто и множество
непусто и множество  состоит только из нулевого вектора, значит решение задачи существует и при
состоит только из нулевого вектора, значит решение задачи существует и при  при фикcированном
при фикcированном 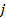 . Пусть
. Пусть  — квантиль уровня
— квантиль уровня 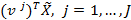 . В силу условия (34), ограничения, соответствующие величинам
. В силу условия (34), ограничения, соответствующие величинам  , являются пассивными. Поэтому их можно исключить из системы ограничений задачи (32), тем самым значительно понизив размерность решаемой задачи.
, являются пассивными. Поэтому их можно исключить из системы ограничений задачи (32), тем самым значительно понизив размерность решаемой задачи.


