Обратной угловой засечкой называется определение положения пункта путем измерения углов или направлений на определяемом пункте не менее чем на три пункта, координаты которых известны.
В том случае, когда исходных пунктов более трех – обратная угловая засечка называется многократной.
Пусть имеется пункт  с неизвестными плановыми координатами
с неизвестными плановыми координатами 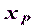 и
и 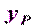 . С пункта
. С пункта 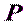 имеется видимость на пункты триангуляции
имеется видимость на пункты триангуляции  ,
,  , …,
, …,  ,.всего
,.всего 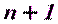 исходный пункт, где
исходный пункт, где 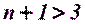 . В этих условиях плановые координаты пункта
. В этих условиях плановые координаты пункта  могут быть определены из обратной угловой засечки. Но поскольку количество исходных пунктов составляет более трех, т.е. имеются избыточно измеренные величины, то засечка в этом случае будет многократной и возникает задача уравнивания обратной многократной угловой засечки.
могут быть определены из обратной угловой засечки. Но поскольку количество исходных пунктов составляет более трех, т.е. имеются избыточно измеренные величины, то засечка в этом случае будет многократной и возникает задача уравнивания обратной многократной угловой засечки.
Будем считать, что при определяемой точке 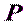 измерено
измерено 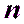 углов
углов  ,
, 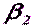 , …,
, …, 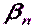 при визировании на
при визировании на 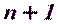 исходный пункт триангуляции. Каждый угол измерен отдельно.
исходный пункт триангуляции. Каждый угол измерен отдельно.
Схема обратной многократной угловой засечки, соответствующей данному случаю, показана на рис. 5.1.
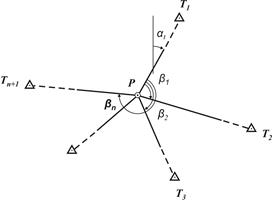
|
| Схема обратной многократной угловой засечки (по измеренным углам)
|
Как было отмечено ранее при рассмотрении вопроса уравнивания прямой многократной угловой засечки, наилучшим вариантом уравнивания применительно к засечкам является уравнивание по методу наименьших квадратов параметрическим способом.
Для этого неизвестные координаты 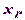 и
и  точки
точки 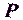 , которые в параметрическом способе носят название параметры, представляем в виде приближенных значений координат
, которые в параметрическом способе носят название параметры, представляем в виде приближенных значений координат 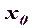 ,
,  и поправок к ним
и поправок к ним 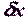 и
и  :
:
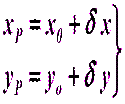 (5.9)
(5.9)
Приближенные координаты пункта  могут быть определены из решения обратной однократной угловой засечки, например, по формулам Деламбра. Поправки к приближенным значениям находятся из уравнивания.
могут быть определены из решения обратной однократной угловой засечки, например, по формулам Деламбра. Поправки к приближенным значениям находятся из уравнивания.
Первым этапом уравнительных вычислений является этап составления параметрических уравнений поправок, в которых измеренные величины представляются в виде функций выбранных неизвестных параметров. Для этого рассмотрим рисунок 5.4.
Здесь точка 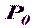 – это приближенное положение определяемой точки, которому соответствуют координаты
– это приближенное положение определяемой точки, которому соответствуют координаты 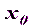 ,
, 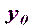 . Точка
. Точка  с координатами
с координатами 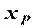 ,
,  – это окончательное или уравненное положение этой же точки. Углы
– это окончательное или уравненное положение этой же точки. Углы  и
и  - приближенные дирекционные углы направлений
- приближенные дирекционные углы направлений  и
и 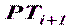 , а
, а 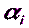 и
и  – окончательные дирекционные углы тех же направлений;
– окончательные дирекционные углы тех же направлений;  – приближенное значение измеренного угла
– приближенное значение измеренного угла  ,
, 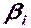 – окончательное (уравненное) значение того же угла.
– окончательное (уравненное) значение того же угла.
Уравненное значение измеренного угла 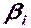 можно представить как измеренное значение плюс поправка, полученная из уравнивания,
можно представить как измеренное значение плюс поправка, полученная из уравнивания,
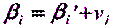 , (5.10)
, (5.10)
либо переписав,
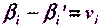 (5.11)
(5.11)
Равенств вида (5.11) будет столько, сколько было измерено углов при точке  .
.
Окончательное значение угла  можно выразить и иначе, через приближенное значение
можно выразить и иначе, через приближенное значение 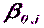 и поправку к нему
и поправку к нему  :
:
 (5.12)
(5.12)
Подставив это значение угла  в формулу (5.11) получим
в формулу (5.11) получим
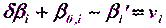 (5.13)
(5.13)
Разность между приближенным значением  и измеренным значением
и измеренным значением 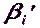 угла
угла  есть свободный член, который обозначается
есть свободный член, который обозначается  :
:
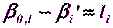 (5.14)
(5.14)
Выражение (5.13) можно теперь переписать в виде
 (5.15)
(5.15)
Теперь нам необходимо выразить поправку 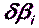 через поправки
через поправки  и
и  .Для этого выразим углы
.Для этого выразим углы  и
и 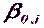 через дирекционные углы
через дирекционные углы 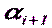 ,
, 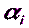 и
и  ,
,  :
:
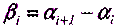 (5.16)
(5.16)
или
 (5.17)
(5.17)
и
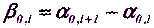 (5.18)
(5.18)
Вычтя теперь из равенства (5.17) равенство (5.18) и обозначив
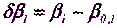 (5.19)
(5.19)
получим:
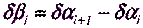 . (5.20)
. (5.20)
Тогда уравнение (5.15) с учетом (5.20) примет вид
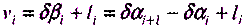 (5.21)
(5.21)
Поправки  и
и  могут быть найдены через дифференциальные формулы дирекционного угла
могут быть найдены через дифференциальные формулы дирекционного угла
 (5.22)
(5.22)
Тогда уравнение (5.21) может быть переписано в виде
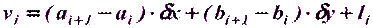 (5.23)
(5.23)
Введя обозначения
 (5.24)
(5.24)
получим окончательное выражение для параметрических уравнений поправок
 (5.25)
(5.25)
Всего будет  таких параметрических уравнений поправок.
таких параметрических уравнений поправок.
Будем решать систему таких уравнений под условием 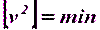 . В результате придем к двум нормальным уравнениям
. В результате придем к двум нормальным уравнениям
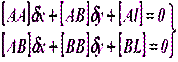 (5.26)
(5.26)
Решая эти уравнения способом определителей получим
 (5.27)
(5.27)
Для получения уравненных значений координат определяемого пункта  найденные поправки
найденные поправки  и
и  необходимо прибавить к приближенным значениям координат, т.е подставить их в формулы (5.9).
необходимо прибавить к приближенным значениям координат, т.е подставить их в формулы (5.9).
Далее вычислив по формулам (5.25) значения поправок  и подставив их в формулы (5.10) получим уравненные значения углов
и подставив их в формулы (5.10) получим уравненные значения углов  ,
,  , …,
, …, 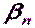 .
.
Для заключительного контроля уравнивания найдем вторично уравненные значения измеренных углов 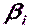 через дирекционные углы (формула (5.16)). Сами значения дирекционных углов найдем из решения обратных геодезических задач. Расхождения в дважды полученных значениях углов
через дирекционные углы (формула (5.16)). Сами значения дирекционных углов найдем из решения обратных геодезических задач. Расхождения в дважды полученных значениях углов  не должны превышать точности вычислений.
не должны превышать точности вычислений.
Вывод: многократная обратная засечка обеспечивает необходимую точность определения планового положения опознака.!!!!



 с неизвестными плановыми координатами
с неизвестными плановыми координатами 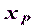 и
и 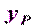 . С пункта
. С пункта 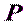 имеется видимость на пункты триангуляции
имеется видимость на пункты триангуляции  ,
,  , …,
, …,  ,.всего
,.всего 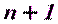 исходный пункт, где
исходный пункт, где 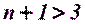 . В этих условиях плановые координаты пункта
. В этих условиях плановые координаты пункта 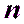 углов
углов  ,
, 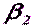 , …,
, …, 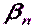 при визировании на
при визировании на 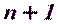 исходный пункт триангуляции. Каждый угол измерен отдельно.
исходный пункт триангуляции. Каждый угол измерен отдельно.
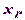 и
и  точки
точки 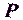 , которые в параметрическом способе носят название параметры, представляем в виде приближенных значений координат
, которые в параметрическом способе носят название параметры, представляем в виде приближенных значений координат 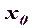 ,
,  и поправок к ним
и поправок к ним 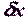 и
и  :
: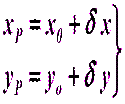 (5.9)
(5.9) могут быть определены из решения обратной однократной угловой засечки, например, по формулам Деламбра. Поправки к приближенным значениям находятся из уравнивания.
могут быть определены из решения обратной однократной угловой засечки, например, по формулам Деламбра. Поправки к приближенным значениям находятся из уравнивания.
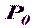 – это приближенное положение определяемой точки, которому соответствуют координаты
– это приближенное положение определяемой точки, которому соответствуют координаты 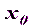 ,
, 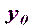 . Точка
. Точка  с координатами
с координатами 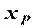 ,
,  – это окончательное или уравненное положение этой же точки. Углы
– это окончательное или уравненное положение этой же точки. Углы  и
и  - приближенные дирекционные углы направлений
- приближенные дирекционные углы направлений  и
и 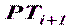 , а
, а 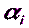 и
и  – окончательные дирекционные углы тех же направлений;
– окончательные дирекционные углы тех же направлений;  – приближенное значение измеренного угла
– приближенное значение измеренного угла  ,
, 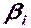 – окончательное (уравненное) значение того же угла.
– окончательное (уравненное) значение того же угла.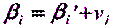 , (5.10)
, (5.10)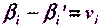 (5.11)
(5.11) можно выразить и иначе, через приближенное значение
можно выразить и иначе, через приближенное значение 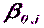 и поправку к нему
и поправку к нему  :
: (5.12)
(5.12)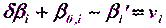 (5.13)
(5.13) и измеренным значением
и измеренным значением 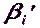 угла
угла  :
: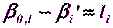 (5.14)
(5.14) (5.15)
(5.15)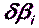 через поправки
через поправки  и
и  .Для этого выразим углы
.Для этого выразим углы 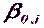 через дирекционные углы
через дирекционные углы 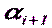 ,
,  ,
,  :
: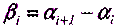 (5.16)
(5.16) (5.17)
(5.17)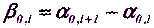 (5.18)
(5.18)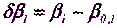 (5.19)
(5.19)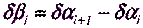 . (5.20)
. (5.20)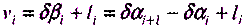 (5.21)
(5.21) и
и  могут быть найдены через дифференциальные формулы дирекционного угла
могут быть найдены через дифференциальные формулы дирекционного угла (5.22)
(5.22)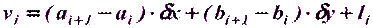 (5.23)
(5.23) (5.24)
(5.24) (5.25)
(5.25) таких параметрических уравнений поправок.
таких параметрических уравнений поправок.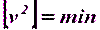 . В результате придем к двум нормальным уравнениям
. В результате придем к двум нормальным уравнениям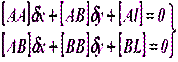 (5.26)
(5.26) (5.27)
(5.27) и
и  необходимо прибавить к приближенным значениям координат, т.е подставить их в формулы (5.9).
необходимо прибавить к приближенным значениям координат, т.е подставить их в формулы (5.9). и подставив их в формулы (5.10) получим уравненные значения углов
и подставив их в формулы (5.10) получим уравненные значения углов  , …,
, …,  .
.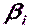 через дирекционные углы (формула (5.16)). Сами значения дирекционных углов найдем из решения обратных геодезических задач. Расхождения в дважды полученных значениях углов
через дирекционные углы (формула (5.16)). Сами значения дирекционных углов найдем из решения обратных геодезических задач. Расхождения в дважды полученных значениях углов  не должны превышать точности вычислений.
не должны превышать точности вычислений.


